GKIW Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 30: | Linia 30: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
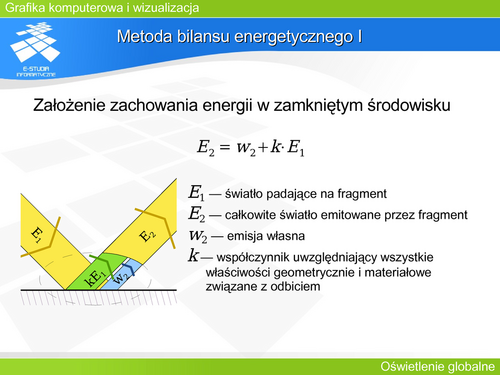
'''Generowanie próbek I''' | |||
Zastosowanie całkowania Monte Carlo wymaga wygenerowania próbek o określonym rozkładzie i w zdefiniowanym obszarze. Niestety programy biblioteczne najczęściej pozwalają uzyskać ciąg próbek pseudolosowych o rozkładzie równomiernym w obszarze prostokątnym jednostkowym. | |||
Generowanie wartości losowych zgodnie z zadanym rozkładem gęstości prawdopodobieństwa może być zrealizowane jedną ze znanych metod. Najczęściej stosuje się metodę funkcji odwrotnej do dystrybuanty lub metodę usuwania próbek niepasujących. | |||
Pierwsza metoda wymaga analitycznego wyznaczenia dystrybuanty na podstawie funkcji gęstości prawdopodobieństwa, a następnie wyznaczenia funkcji odwrotnej. Uzyskana funkcja przelicza próbki o rozkładzie równomiernym na próbki o zadanym rozkładzie. Metoda ta jest bardzo efektywna, ale nie zawsze możliwe jest wyznaczenie odpowiedniej funkcji odwrotnej. | |||
|} | |} | ||
---- | ---- | ||
| Linia 36: | Linia 42: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd5.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Generowanie próbek II''' | |||
Dobrym przykładem wykorzystania metody funkcji odwrotnej do dystrybuanty jest wygenerowanie próbek o rozkładzie równomiernym w kole o zadanym promieniu. | |||
Wydawać by się mogło, że najprostszym rozwiązaniem takiego zadania będzie wygenerowanie próbek w prostokącie jednostkowym a następnie przeliczenie ich współrzędnych do współrzędnych biegunowych. Takie rozwiązanie nie daje rozkładu równomiernego w kole. | |||
Można to natomiast osiągnąć stosując metodę funkcji odwrotnej do dystrybuanty. Podane wzory pokazują przeliczenie współrzędnych z układu prostokątnego (gdzie są wygenerowane próbki pseudolosowe o rozkładzie równomiernym w prostokącie jednostkowym) na układ biegunowy koła, Takie przeliczenie zapewnia równomierność rozkładu próbek w kole. | |||
|} | |} | ||
---- | ---- | ||
| Linia 42: | Linia 54: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd6.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
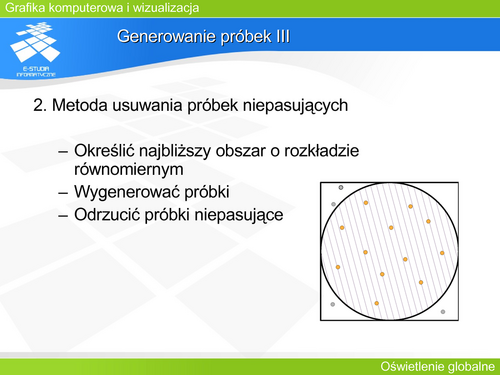
'''Generowanie próbek III''' | |||
Metoda usuwania próbek niepasujących wymaga zdefiniowania obszaru (prostokąta) obejmującego zadany obszar i wygenerowania próbek o rozkładzie równomiernym. Oczywiście część z nich będzie poza zadanym obszarem – należy je odrzucić. Metoda ta może być praktycznie zawsze zastosowana – nie ma żadnych ograniczeń ani problemów analitycznych. Nie jest ona jednak efektywna, gdyż wymaga generowania dużej liczby próbek, które nie są potem wykorzystywane. | |||
Rysunek pokazuje zastosowanie tej metody do generowania próbek w kole, część próbek leżących poza obszarem koła zostaje odrzucona. | |||
|} | |} | ||
---- | ---- | ||
| Linia 48: | Linia 65: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
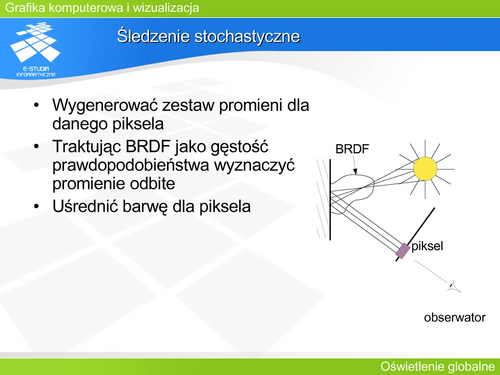
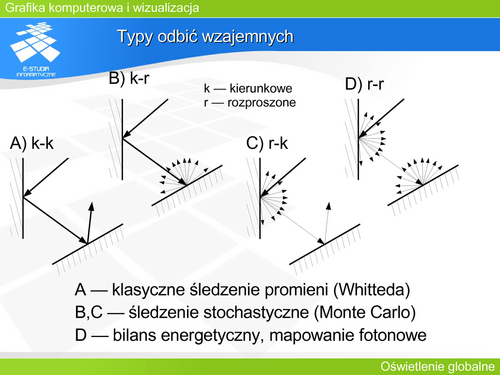
'''Śledzenie stochastyczne''' | |||
W śledzeniu stochastycznym generowanych jest wiele promieni (9, 16 lub nawet więcej) na piksel. Każdy z promieni może pójść własną drogą – to znaczy dla każdego będzie analizowane inne drzewo przecięć. Barwa piksela jest uśrednieniem tych promieni. Odbicie (załamanie) promienia trafiającego w powierzchnię obiektu zależy od funkcji BRDF traktowanej jako gęstość prawdopodobieństwa. | |||
Wygenerowanie promieni przechodzących przez piksel w sposób zdeterminowany w regularnej siatce powoduje powstanie takich samych zniekształceń intermodulacyjnych jak w klasycznym śledzeniu (efekt schodkowy, mory na obszarach pokrytych teksturą). Aby temu zaradzić można generować próbki losowo na obszarze piksela. Jednak w tym przypadku pojawia się bardzo silny szum nakładający się na wyznaczone barwy. Najlepszym rozwiązaniem byłoby wygenerowanie próbek w taki sposób, aby utrzymać między nimi pewną minimalną odległość. Spowodowałoby to znaczną redukcję amplitudy szumu. Niestety takie rozwiązanie jest zbyt kosztowne obliczeniowo. Dobrym kompromisem (i najczęściej stosowanym) jest generowanie próbek na regularnej siatce, ale z dodatkiem przypadkowych przesunięć (ang. jittering sampling lub stratified sampling). Jest to proste obliczeniowo i jednocześnie jeśli przesunięcia są nieskorelowane, to występuje znacząca redukcja szumu przy minimalnych zniekształceniach intermodulacyjnych. | |||
Zastosowanie próbkowania stochastycznego pozwala traktować wyznaczenie barwy piksela jako całkowanie po obszarze piksela. Dzięki temu możliwe jest uzyskanie miękkich cieni i rozmycia odbicia światła, możliwe jest uwzględnienie odbić nieidealnych kierunkowo i rozproszonych. | |||
Wadą takiego rozwiązania jest pojawiający się szum, który można redukować przez zwiększenie liczby promieni, co z kolei, niestety, pociąga za sobą zwiększenie czasu realizacji. | |||
Warto pamiętać, że dzisiaj przyjęło się, że jeśli występuje nazwa „metoda śledzenia promieni” bez dodatkowych określeń to jest to rozumiane właśnie jako śledzenie stochastyczne, a nie klasyczne Whitteda. | |||
|} | |} | ||
---- | ---- | ||
| Linia 54: | Linia 79: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd8.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
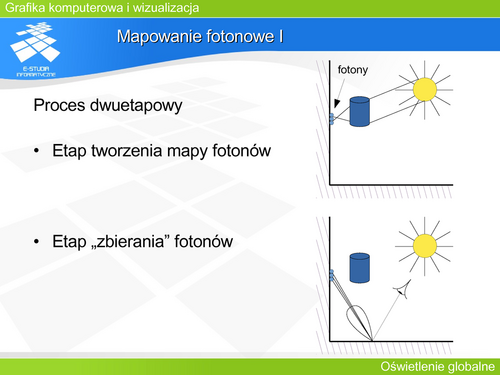
'''Mapowanie fotonowe I''' | |||
Etap1. '''Rozsyłanie fotonów'''. Na powierzchni źródła generowane są fotony, które są rozsyłane zgodnie z kierunkiem rozchodzenia się światła. Symuluje to emisję światła przez powierzchnię źródła. Ruch wyemitowanych fotonów odbywa się zgodnie z zasadami optyki geometrycznej. Zjawiska odbicia i przenikania (załamania) są opisane za pomocą odpowiednich modeli matematycznych (BRDF ). Każdy foton pokonuje pewną drogę napotykając na niej kolejne powierzchnie. Na każdej z nich, przy każdym odbiciu lub załamaniu, foton może pozostawić część swojego strumienia. W ten sposób z tych „pozostałości” powstaje mapa fotonowa. Struktura danych tej mapy obejmuje nie tylko wartość pozostawionego w danym punkcie strumienia, ale także parametry geometryczne – współrzędne punktu i kierunek padania fotonu. | |||
Etap2. '''Zbieranie fotonów'''. Aby stworzyć obraz, przez każdy piksel ekranu jest prowadzony promień zgodnie ze zdefiniowanym sposobem patrzenia przez obserwatora (zgodnie z odpowiednim rzutowaniem). Droga tego promienia jest następnie analizowana tak jak w klasycznym śledzeniu promieni. Luminancja danego piksela jest wyznaczana tak jak w śledzeniu stochastycznym, ale całkowaniu Monte Carlo podlegają zgromadzone na danej powierzchni fotony. | |||
Mapowanie fotonowe zostało stworzone jako mechanizm uzupełniający śledzenie promieni w celu symulacji zjawisk takich jak np., skupienie światła oraz uwzględnienie nieidealnych właściwości odbijających zarówno powierzchni rozpraszających jak i lustrzanych. | |||
|} | |} | ||
---- | ---- | ||
| Linia 60: | Linia 93: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd9.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Mapowanie fotonowe II''' | |||
Przykłady obrazów wygenerowanych z wykorzystaniem mapowania fotonowego. Dzięki zastosowaniu tej techniki w metodzie śledzenia promieni możliwe stało się uzyskanie takich efektów jak rozproszenie światła za szklanką z płynem na lewym rysunku, oraz skupienia światła (caustic) na rysunku środkowym i prawym. | |||
|} | |} | ||
---- | ---- | ||
| Linia 66: | Linia 103: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd10.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd10.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
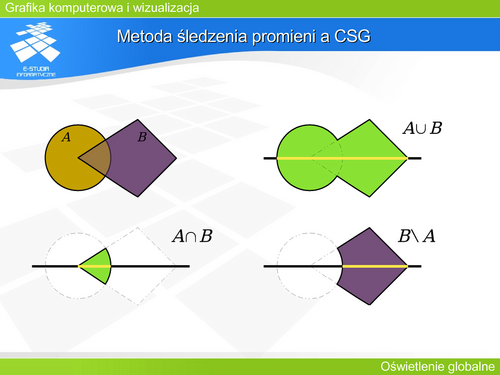
'''Metoda śledzenia promieni a CSG''' | |||
Warto zauważyć, że omawiana wcześniej metoda modelowania – konstrukcyjna geometria brył może być bezpośrednio połączona z metodą śledzenia promieni. Jeśli zachodzi pewien mechanizm operacji wolumetrycznej modelowania, na przykład określenie części wspólnej (iloczynu) obiektów A i B, to operacja ta również odnosi się do prostej będącej analizowanym promieniem w metodzie śledzenia. Przy czym odniesienie tego do promienia oznacza operację na odcinkach o końcach wyznaczonych przecięciem promienia z powierzchnią obiektów. Wyznaczenie operacji wolumetrycznych odcinków na prostej jest zadaniem bardzo prostym. W takim razie nie jest w ogóle potrzebne niezależne wyznaczanie powierzchni będących rezultatem operacji wolumetrycznych. Można to zrobić podczas rysowania obrazu. Wystarczy, że analizując przecięcia dla każdego promienia zostanie uwzględniony mechanizm modelowania obiektu metodą konstrukcyjnej geometrii brył i wyznaczone odpowiednie punkty przecięć. | |||
|} | |} | ||
---- | ---- | ||
| Linia 71: | Linia 112: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd11.png|thumb|500px]] | ||
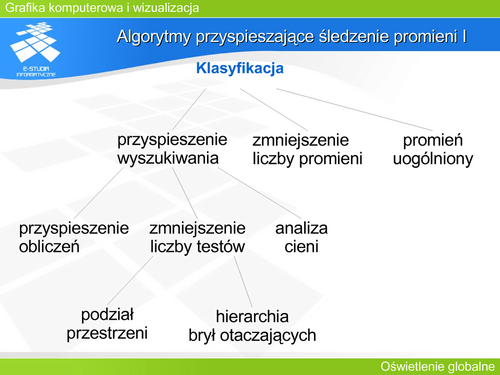
|valign="top"| | '''|valign="top"| | ||
Algorytmy przyspieszające śledzenie promieni I''' | |||
Barwa każdego piksela obrazu jest wyznaczana w podobny sposób przez analizę odpowiedniego drzewa przecięć. Liczba operacji z tym związanych rzutuje na czas obliczeń całości. Z drugiej strony można wskazać operacje, które pojawiają się najczęściej – są to z reguły operacje związane z szukaniem przecięcia promienia z powierzchnią obiektu. Stąd algorytmy przyspieszające metodę śledzenia próbują zredukować koszty obliczeń albo przez przyspieszenie wyznaczania przecięć, albo przez zmniejszenie nakładu pracy związanej z analizą drzewa. | |||
|} | |} | ||
---- | ---- | ||
| Linia 78: | Linia 123: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd12.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd12.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Algorytmy przyspieszające śledzenie promieni II''' | |||
Metody te koncentrują się z jednej strony na operacjach numerycznych, a z drugiej na technice wyboru promieni do analizy. Stosowane operacje matematyczne i uproszczenia opisu mają na celu wyłącznie zmniejszenie powtarzanych obliczeń. Odbywa się to przez wyznaczenie wartości pewnych wyrażeń (wybierane są takie wyrażenia, których wartości są niezależne od równania promienia) w preprocesingu przed analizą biegu promienia. Wyniki tych obliczeń są później wykorzystywane w trakcie śledzenia promieni. Dzięki temu unika się wielokrotnego powtarzania tych samych operacji matematycznych. Oczywiście możliwość optymalizacji tą drogą wymaga dość żmudnej analizy równań powierzchni, a efektywność przyspieszenia bardzo ściśle zależy od opisu powierzchni. Nie prowadzi to natomiast do przybliżenia ani zmiany wartości obliczeń końcowych. | |||
|} | |} | ||
---- | ---- | ||
| Linia 84: | Linia 133: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M9_Slajd13.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Algorytmy przyspieszające śledzenie promieni III''' | |||
Stwierdzenie czy promień przecina dany obiekt jest zadaniem trudnym. Zastosowanie odpowiedniej techniki wyboru promieni, które mają szansę na przecięcie, pozwala wyeliminować zbędne przypadki, dla których nie trzeba przeprowadzać długiej i kosztownej, pełnej analizy biegu promienia. | |||
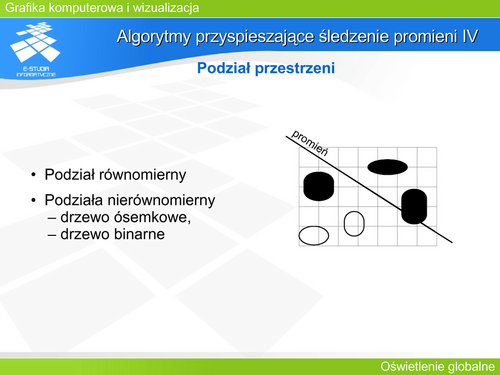
Techniki wyboru promieni można podzielić na dwie grupy: zastosowanie brył otaczających i podział przestrzeni. | |||
W pierwszym przypadku (bryły otaczające) zanim rozpocznie się wyznaczanie przecięcia promienia z powierzchnią obiektu, można spróbować wyznaczyć przecięcie z bryłą otaczającą obiekt. Jeśli promień nie przecina takiej bryły, to analiza przecięcia z obiektem nie jest konieczna. Oczywiście aby w takiej sytuacji można było mówić o przyspieszeniu obliczeń powinny być spełnione dwa warunki. Bryła powinna „ściśle” (ciasno) otaczać obiekt oraz wyznaczenie przecięcia promienia z bryłą powinno być wielokrotnie prostsze (i szybsze) niż przecięcia z obiektem. Często te warunki są sprzeczne. Najczęściej stosuje się kule, wielościany lub „pasy” równoległych płaszczyzn jako bryły otaczające. Kula jest obiektem, dla której najszybciej można stwierdzić, czy jest przecięta prostą czy nie. Wystarczy znaleźć odległość prostej od środka kuli i porównać z promieniem. Jest to szybsze niż sprawdzanie przecięcia prostej z prostopadłościanem. Wadą kuli jako obiektu otaczającego jest najczęściej niezbyt ciasne obejmowanie obiektu. Warto zwrócić uwagę na przecięcia z obiektami typu AABB (ang. Axis-Aligned Bounding Box - prostopadłościan o krawędziach wyznaczonych przez proste równoległe do osi układu współrzędnych) i OBB (ang. Oriented Bounding Box - prostopadłościan dowolnie zorientowany) Aby zwiększyć efektywność działania metody można skonstruować hierarchię brył otaczających. | |||
|} | |} | ||
---- | ---- | ||
Wersja z 10:32, 30 paź 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |