GKIW Moduł 9

---

---

Definicja Modelowanie lokalnego odbicia (lub przenikania) światła nosi czasem nazwę problemu oświetlenia lokalnego. Uwzględnia bowiem tylko lokalne właściwości powierzchni. Problem oświetlenia globalnego jest natomiast opisem zależności związanych z rozchodzeniem się światła, ale uwzględniającym wzajemne oddziaływanie między powierzchniami – np. wielokrotne odbicie światła między różnymi przedmiotami. Próby rozwiązania tego problemu na poziomie modelu odbicia lokalnego sprowadzały się do uwzględnienia średniej wartości oświetlenia we wszystkich punktach sceny – oświetlenia tła. Taka składowa jest uwzględniona w modelu Phonga. W grafice komputerowej stosowane są dwie ogólne metody rozwiązania problemu oświetlenia globalnego: - Metoda śledzenia promieni, - Metoda bilansu energetycznego.

---

---

---

---

---

---

---

---

---

---

---

Ogólne równanie renderingu Kajiya Transport światła odbywa się na scenie na drodze wielokrotnych odbić od poszczególnych fragmentów powierzchni. Ogólne równanie renderingu opisuje zależność między oświetleniem wzajemnym elementarnych fragmentów powierzchni. Rozpatrując dwa fragmenty $x$ i $x^{\prime }$ określamy transport od $x^{\prime }$ do $x$. Równanie uwzględnia przy tym zarówno emisję własną fragmentu $x^{\prime }$ jak i odbicie przez $x^{\prime }$. Takie sformułowanie daje możliwość zbudowania zależności rekurencyjnej między wszystkimi fragmentami sceny. Z drugiej strony jeśli podzielić całą scenę na fragmenty elementarne, to uwzględnienie równania renderingu wymaga analizy „każdy z każdym” tych fragmentów. Prowadzi to oczywiście do złożoności kwadratowej problemu oświetlenia globalnego. Równanie wizualizacji zaproponowane przez Kajiya z 1986 roku pozwala prześledzić rekurencyjnie drogę promieni i wyznaczyć intensywności oświetlenia określonych powierzchni. Uwzględnienie wielkości świetlnych doprowadziło do powstania luminancyjnego równania wizualizacji opisywanego przez Cohena w 1993. Pozwala prowadzić obliczenia w grafice komputerowej z uwzględnieniem zasad fizyki. Po uwzględnieniu wielkości świetlnych luminancyjne równanie wizualizacji wyznacza rozkład luminancji.

---

---

---

---

---

---

---

---

---

---

---

Typy odbić wzajemnych Dobrą klasyfikacją zachowania się algorytmów oświetlenia globalnego jest klasyfikacja pokazująca w jaki sposób są implementowane wzajemne odbicia między dwiema powierzchniami. Biorąc pod uwagę dwa rodzaje odbicia: rozproszone i kierunkowe, możemy mieć do czynienia z czterema możliwościami odbić wzajemnych. Kierunkowe-kierunkowe – jest to implementowane przez klasyczną metodę śledzenia promieni (Whitteda). I praktycznie metoda klasyczna śledzenia nie pozwala na opis innych odbić wzajemnych. Rozproszone-rozproszone – jest to implementowane przez klasyczną metodę energetyczną. Podobnie jak śledzenie, klasyczna metoda energetyczna nie pozwalana na implementację innych wariantów odbić. Rozproszone-kierunkowe (także kierunkowe-rozproszone) – może być implementowane w nowszych rozwiązaniach metody śledzenia.

---

---

---

---

---

---

---

Metoda śledzenia promieni I Traktując model kamery jako mechanizm realizacji rzutowania perspektywicznego, można zauważyć, że barwa danego piksela ekranu powstaje dzięki światłu docierającemu do niego z kierunku wynikającego z rzutowania. Można zatem prześledzić „drogę światła”, które dociera do piksela i na tej podstawie wyznaczyć barwę. Metoda śledzenia promieni polega na analizie przebiegu promieni między obserwatorem a źródłem światła. Drogę promieni opisuje drzewo przecięć, którego węzły reprezentują zjawiska jakie zachodzą między promieniem a powierzchniami obiektów. Korzeń drzewa odpowiada promieniowi docierającemu do obserwatora zaś liście — źródłom światła. Zjawiska odbicia, przenikania i pochłaniania opisane są odpowiednimi modelami matematycznymi. Wyznaczenie barwy danego piksela polega na analizie odpowiedniego drzewa.

---

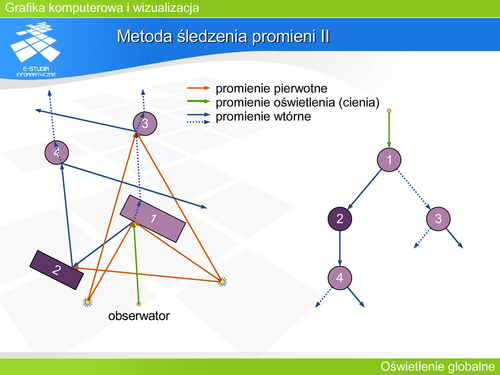
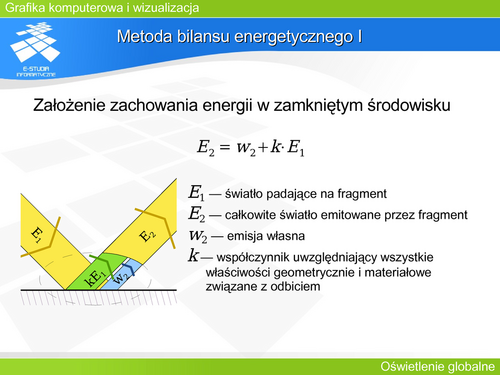
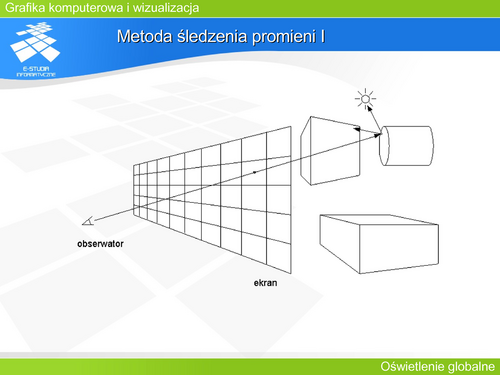
Metoda śledzenia promieni II Analizę „drogi światła” prowadzi się od obserwatora (kamery – środka rzutowania) do obiektów na scenie – to znaczy w kierunku przeciwnym do rzeczywistego rozchodzenia się światła. Stąd czasami metodę nazywa się metodą (śledzenia) promienia odwrotnego. Każde napotkanie obiektu przez promień (promień pierwotny) wymaga analizy. Zawsze jest wyznaczany promień odbity o kierunku zależnym od powierzchni obiektu. Jeśli obiekt jest przezroczysty, to wyznaczany jest promień załamany (promień przechodzący przez obiekt) o kierunku zależnym od właściwości materiałowych obiektu. Oba promienie: odbity i załamany nazywane są promieniami wtórnymi. Zawsze są również wyznaczane tak zwane promienie cienia (czasami nazywane promieniami oświetlenia) w kierunku każdego źródła światła. Promienie cienia pozwalają wyznaczyć oświetlenie danego elementu obiektu przez źródła światła, oczywiście jeśli na drodze promienia cienia do źródła światła jest inny obiekt nieprzezroczysty (źródło jest zasłonięte) to oświetlenie nie jest liczone. Promienie wtórne mogą wskazać następne przecięcia z obiektami, stając się wtedy promieniami pierwotnymi kolejnej analizy. Tak stworzone drzewo promieni jest obliczane metodą zstępującą, Barwa każdego węzła jest liczona jako funkcja barwy potomków. Gałąź w takim drzewie kończy się, gdy promienie wtórne (odbite i załamane) nie przecinają się z kolejnymi obiektami. Możne też być stosowane inne zakończenie procesu budowy i/lub analizy drzewa: gdy osiągnięto określony/zadany poziom rekurencji, albo po prostu gdy zabrakło pamięci na następne poziomy.

---

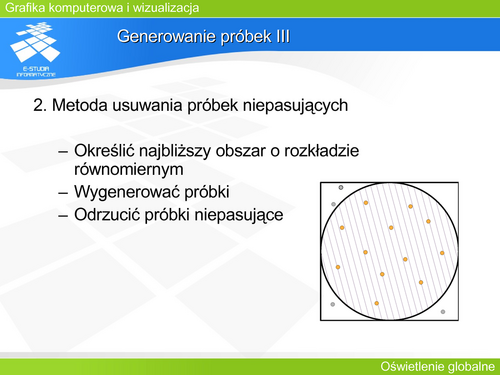
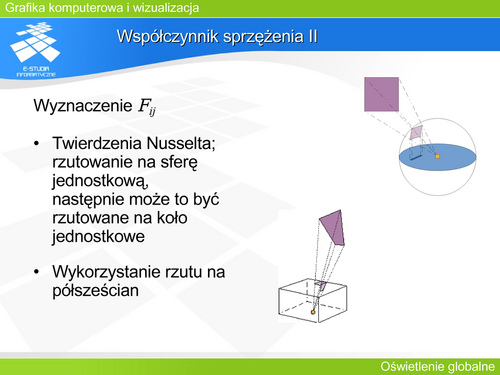
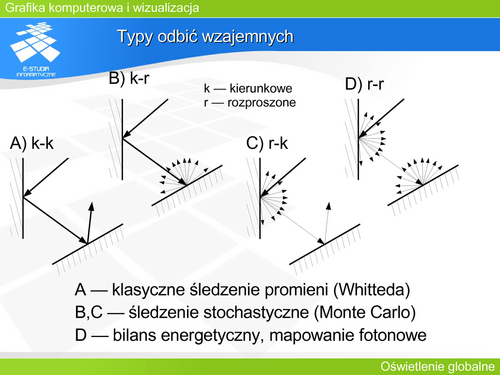
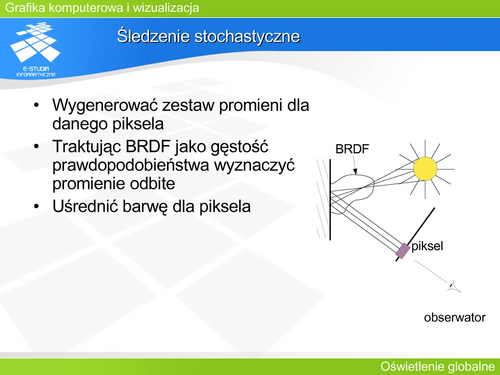
Metoda śledzenia promieni III Istnieje kilka różnych wersji realizacji tego algorytmu: - Śledzenie klasyczne (Whitteda), polegające na analizie pojedynczego promienia poczynając od obserwatora - odwrotnie niż rzeczywiste rozchodzenie się światła, - Śledzenie stochastyczne, kiedy promienie wysyłane są na zasadzie próbkowania pewnego obszaru, również odbicie (załamanie) światła jest modelowane na zasadzie funkcji prawdopodobieństwa, która określa w którym kierunku odbije się (załamie) promień. - Śledzenie dwukierunkowe, kiedy analiza jest przeprowadzana w obu kierunkach: poczynając od obserwatora i poczynając od źródła światła. 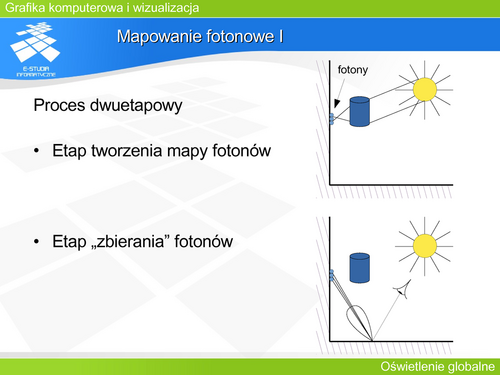- Mapowanie fotonowe (Jensena) jest śledzeniem dwukierunkowym rozszerzonym o tworzenie pośrednich źródeł światła na powierzchniach rozpraszających. Rozwój możliwości metody śledzenia promieni polega na dodawaniu coraz bardziej skomplikowanych przypadków, które mogą się pojawić na drodze promienia pomiędzy źródłem a obserwatorem. Najprościej jest opisać przebieg odbicia kierunkowego (lustrzanego), najtrudniej wielokrotne odbicie rozproszone i pośrednie oddziaływania typu składowej kierunkowej padającej na powierzchnię rozpraszającą.

---

Śledzenie klasyczne (Whitteda) Śledzenie klasyczne (Whitteda) odpowiada dokładnie opisanemu procesowi budowy i analizy drzewa promieni. Warto zauważyć, że opisany sposób analizy drzewa promieni odpowiada tak naprawdę kierunkowemu rozchodzeniu się światła. Oznacza to, że dobre efekty takiej analizy uzyskać można dla obiektów, które charakteryzują się właśnie kierunkowym charakterem odbicia i przenikania. Pierwsze rysunki wygenerowane przez Whitteda wzbudziły podziw gdyż pokazywały w sposób perfekcyjny załamanie światła przez sferyczne szklane obiekty. Podstawowym problemem śledzenia klasycznego ( i tak naprawdę każdej późniejszej modyfikacji metody) jest szybkie wyznaczenie przecięcia promienia z obiektem.

---

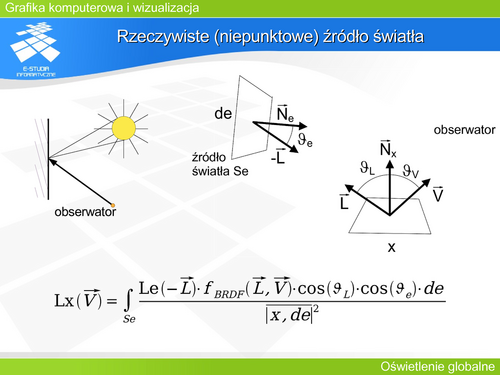
Rzeczywiste (niepunktowe) źródło światła Problem z opisem rzeczywistych obiektów za pomocą klasycznego śledzenia Whitteda zaczyna się pojawiać gdy weźmiemy pod uwagę rzeczywiste źródło światła (o skończonych – niepomijalnych rozmiarach). Analiza oświetlenia na drodze jednego promienia przestaje odpowiadać rzeczywistości. Osiągnięcie obrazu miękkiego półcienia jest całkowicie niemożliwe. Rozpatrując fragment powierzchni oświetlony bezpośrednio przez źródło powierzchniowe i biorąc pod uwagę równanie wizualizacji Kajiya, można wykazać, że luminancja $LX(\breve{V})$ postrzegana na powierzchni $x$ z kierunku wektora $\breve{V}$ będzie opisana przedstawionym równaniem. Poprawny wynik może dać tylko analiza uwzględniająca całkowanie powierzchni źródła światła. Przykładem dobrej aproksymacji przy wykorzystaniu klasycznej metody śledzenia jest model Verbecka i Greenberga z 1984 roku. Zakłada on, że źródło powierzchniowe jest przybliżone zbiorem źródeł punktowych rozłożonych na powierzchni źródła.

---

Całkowanie Monte Carlo Rozwiązanie analityczne równania renderingu praktycznie nie ma sensu. Autorzy publikacji dotyczących tego tematu czasami sugerują możliwość rozwiązania analitycznego dla wybranego; wydzielonego i wyizolowanego problemu obejmującego na przykład pojedyncze elementy odbijające i jedno źródło światła o prostym opisie geometrycznym. Dla bardziej skomplikowanych scen trudności pojawiają się już na etapie opisu wzajemnego zasłaniania i kształtu jednego elementu widzianego z powierzchni drugiego. Dobrym rozwiązanie w takiej sytuacji – rozwiązaniem uniwersalnym jest zastosowanie całkowania Monte Carlo. Na przykład dla problemu pojedynczego powierzchniowego źródła światła można wygenerować zbiór promieni biegnących w kierunku odwrotnym od obserwatora do powierzchni i dalej odbijających się zgodnie z pewnym prawdopodobieństwem zależnym od właściwości odbiciowych powierzchni. Promienie odbite trafią (lub nie) w określony punkt powierzchni źródła, z którym to punktem będzie związana określona luminancja i barwa. Jeśli na podstawie analizy zachowania się takich promieni wyznaczymy wartość luminancji postrzeganej przez obserwatora to zadanie jest rozwiązane. Taką właśnie możliwość daje w tym przypadku całkowanie Monte Carlo. W najprostszym przypadku jednowymiarowym, jeśli chcemy obliczyć całkę $I=\underset{0}{\overset{1}{\int }}h(y)dy$ to możemy skorzystać z N liczb losowych o rozkładzie równomiernym $x_1,x_2,,,,x_N$, stanowiących pewną realizację zmiennej losowej $X$. Wtedy Parser nie mógł rozpoznać (błąd składni): {\displaystyle I \approx \frac{1}{N} \\sum_{i=1}^N h(x_i)} Oczywiście takie proste całkowanie nie byłoby przydatne, gdyż w praktyce problem zachodzi w pewnym przedziale $S$ i jednocześnie wymagane jest losowanie próbek o rozkładzie innym niż równomierny. Podane wzory określają takie rozwiązanie. Warto zwrócić uwagę na zależności dotyczące błędu estymacji całki metodą Monte Carlo. Można pokazać, że wariancja estymacji jest proporcjonalna do $\frac{1}{\sqrt{N}}$ natomiast odchylenie standardowe do $\frac{1}{\sqrt{N}}$. W związku z tym, jeśli chcemy zmniejszyć błąd o połowę to $N$ musi wzrosnąć czterokrotnie.

---