GKIW Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 143: | Linia 143: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd15.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Model Orena i Nayara (1994 r.)''' | |||
Oren i Nayar zwrócili uwagę na rozkład postrzeganej luminancji na rzeczywistych powierzchniach rozpraszających. Zastosowanie modelu odbicia Lambertowskiego (opisu idealnego odbicia rozproszonego) powoduje. że efekt często całkowicie odbiega od rzeczywistego. Jest to spowodowane przede wszystkim rzeczywistym odbiciem rozproszonym, które odbiega od modelu Lambertowskiego. Rzeczywiste obiekty (np. porcelana nieszkliwiona) odbijają w taki sposób, że luminancja odbicia jest większa niż w modelu Lambertowskim. | |||
Oren i Nayar opracowali model, w którym przybliżyli powierzchnię obiektu powierzchnią wielościenną. Założyli, że obiekt pokryty jest wgłębieniami typu V podobnie jak w modelu Cooka-Torrance’a (i Sparrowa). Przy czy w modelu Orena i Nayara mikropowierzchnie nie są lustrzane ale rozpraszają w sposób lambertowski. To znaczy dla każdej pojedynczej mikropowierzchni jest stosowany Lambertowski model odbicia. | |||
Dla takiego modelu powierzchni zastosowali rozkład Gaussa kierunku wektora normalnego do powierzchni wielościennej. W efekcie uzyskali model uwzględniający wzajemne zasłanianie powierzchni wielościennej typu V ale przy lambertowskim odbiciu od mikropowierzchni. Ponieważ uzyskany opis był zbyt skomplikowany do zastosowań praktycznych, zaproponowali aproksymację prostymi równaniami. | |||
|} | |} | ||
---- | ---- | ||
| Linia 149: | Linia 155: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd16.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd16.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Model Ashikhmina i Shirleya (2000r.) I''' | |||
Model Ashikhmina I Shirleya jest współczesnym modelem odbicia. | |||
Spełnia wszystkie podstawowe wymagania (zasada wzajemności, zasada zachowania energii, uwzględnia współczynnik Fresnela odbicia światła). | |||
Pozwala uwzględnić anizotropię odbicia. | |||
Został sformułowany w taki sposób, że może być wykorzystywany w dowolnych obliczeniach graficznych – także we wszystkich wariantach metody śledzenia promieni. (Model He nie może być wykorzystywany w algorytmach typu Monte Carlo.) | |||
Ma dodatkowo jeszcze jedną zaletę: jest modelem atrakcyjnym obliczeniowo. | |||
|} | |} | ||
---- | ---- | ||
| Linia 155: | Linia 169: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd17.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd17.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Model Ashikhmina i Shirleya (2000 r.) II''' | |||
Model Ashikhmina I Shirleya opisuje także odbicie rozproszone. Pozwala je opisać w sposób bliższy zmianom rzeczywistym niż teoretyczny opis Lamberta. | |||
Jednocześnie trzeba podkreślić, że jest to inne podejście do opisu odbicia rozproszonego niż w modelu Orena i Nayara. W modelu Ashikhmina I Shirleya wykorzystano opis oparty na pomyśle Schlicka aproksymacji wielomianowej. | |||
|} | |} | ||
---- | ---- | ||
| Linia 161: | Linia 180: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd18.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
---- | ---- | ||
| Linia 167: | Linia 187: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd19.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd19.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
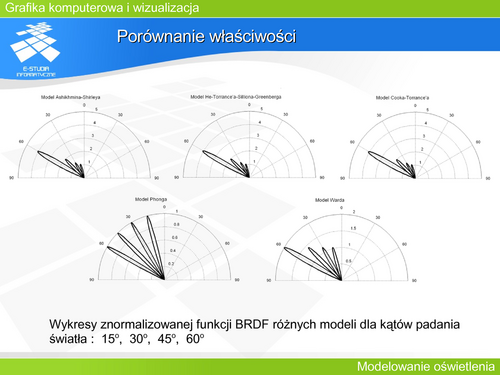
Porównanie właściwości | |||
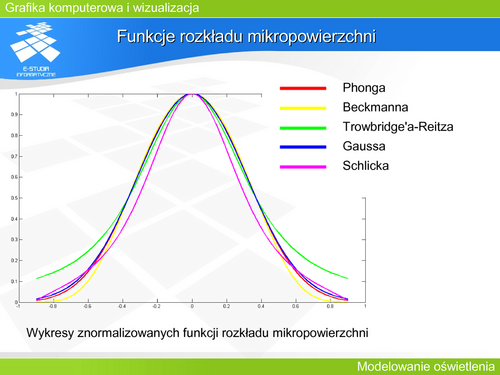
Rysunek przedstawia zmianę kształtu funkcji odbicia w zależności od kąta padania światła dla przykładowych wartości parametrów. Aby możliwe było porównanie różnych modeli odbicia przeprowadzono przeliczenie parametrów między modelami w taki sposób, aby uzyskać zgodność dla kątów odpowiadających połowie wartości funkcji. – Takie postępowanie opisał Blinn w 1977 roku dla funkcji rozkładu mikropowierzchni. Jednocześnie dokonano normalizacji funkcji dla zerowego kąta padania światła. Dzięki temu możliwe staje się zastąpienie jednej funkcji drugą. Możliwe jest także porównanie kształtów – właściwości poszczególnych funkcji. | |||
Jak widać modele '''Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga i Warda''' wykazują zbliżone kształty funkcji BRDF dla różnych kątów padania światła. Przy czym zależności '''Warda''' dają inne proporcje zależności kątowych. Model ten nie uwzględnia współczynnika Fresnela. Stąd wartości maksymalne w opisie Warda odbiegają od wartości w modelach '''Cooka-Torrance’a, Ashikhmina-Shirleya, He-Torrance’a-Silliona-Greenberga'''. | |||
Jako punkt odniesienia przyjmuje się model '''He-Torrance’a-Silliona-Greenberga'''. Badania doświadczalne pokazały, że najlepiej opisuje on zachowanie rzeczywistych powierzchni. Niemniej jednak ze względu na złożoność obliczeniową i jednocześnie bardzo zbliżone właściwości (rysunek) modele '''Cooka-Torrance’a''' oraz '''Ashikhmina-Shirleya''' są atrakcyjniejsze. Warto pamiętać jednocześnie, że model '''He-Torrance’a-Silliona-Greenberga''' nie może być stosowany w odmianach metody śledzenia promieni, gdzie wymagana jest funkcja gęstości prawdopodobieństwa. | |||
Model '''Phonga''' nie pasuje do pozostałych, gdyż w ogóle nie uwzględniono w nim ani kąta padania, ani współczynnika Fresnela. | |||
|} | |} | ||
---- | ---- | ||
| Linia 173: | Linia 200: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd20.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd20.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
'''Inne sposoby opisu BRDF''' | |||
Modele analityczne zaprezentowane dotychczas są bardzo wygodne do zastosowań praktycznych, jednak często nie dają możliwości opisu skomplikowanej - rzeczywistej powierzchni odbijającej. Stosuje się kilka sposobów bardziej złożonych. | |||
Modele wielowarstwowe (np. model Hanrahana i Kreugera z 1993 roku). Wiele obiektów odbija światło wielowarstwowo. Z jednej strony materiały dielektryczne odbijają w sposób rozproszony dzięki tak zwanemu odbiciu objętościowemu. Światło wnika w materiał i po wielokrotnych odbiciach od cząstek materiału, część tego światła wychodzi na zewnątrz, tworząc składową rozproszoną odbicia. Z drugiej strony często mamy do czynienia z materiałami zbudowanymi z warstw o różnej przenikalności światła (i innych właściwościach odbiciowych). Dobrym przykładem jest skóra, której naturalna barwa jest bardzo trudna do uzyskania bez modeli wielowarstwowych. Do tego dochodzą materiały po prostu pokryte farbami lub innymi warstwami zmieniającymi właściwości odbiciowe. | |||
Zamiast próbować modelować skomplikowaną strukturę i właściwości powierzchni można zmierzyć właściwości odbiciowe i na tej podstawie zbudować tablicowaną funkcję BRDF. Oczywiście problem polega na tym, że żeby model pomiarowy był użyteczny to pomiary musza być dokonane z rozdzielczością wymaganą w obliczeniach związanych z danym obrazem i obiektem. Z drugiej strony wybrana próbka musi być reprezentatywna dla danego materiału. | |||
Jeżeli funkcję BRDF potraktować jako funkcję kątów w układzie sferycznym, to naturalnym sposobem opisu, będzie aproksymacja w postaci harmonicznych sferycznych (np. prace Westina z 1992 roku). Dzięki temu można rozłożyć opis odbicia na zestaw składowych, które mogą być używane z określoną dokładnością. Jeśli nie są potrzebne szczegóły powierzchni to można użyć prostszego zestawu opisu funkcji BRDF – bez składowych wyższych harmonicznych. | |||
Stosowane są również inne formy opisu aproksymacji: z wykorzystaniem wielomianów Zernike lub metodami falkowymi. | |||
|} | |} | ||
---- | ---- | ||
| Linia 179: | Linia 217: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd21.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd21.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
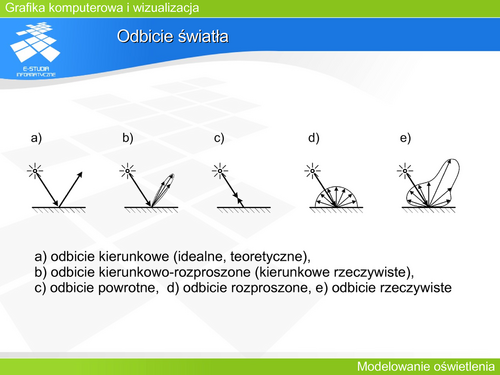
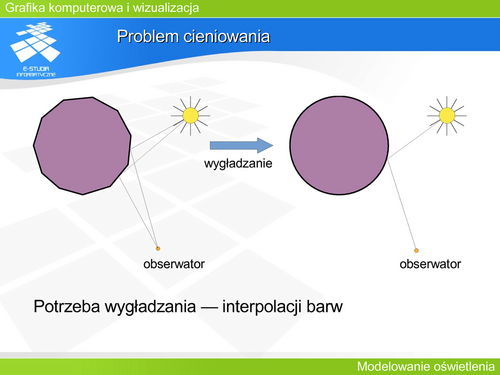
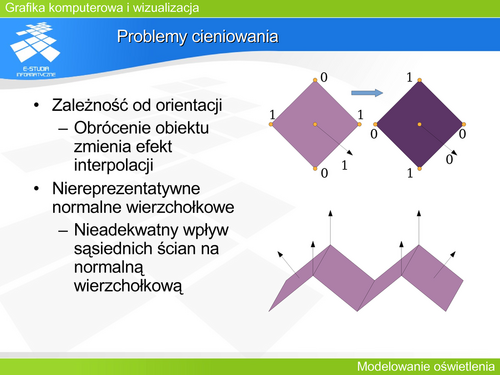
Problem cieniowania | |||
Wyznaczenie barwy związanej z modelem oświetlenia dla każdego punktu/piksela jest zadaniem kosztownym. Można zatem rozpatrywać cieniowanie (interpolację) które pozwoli wypełnić barwą wielokąty w sposób uproszczony. Stosuje się trzy warianty takiego wypełnienia – trzy warianty cieniowania. | |||
- Cieniowanie płaskie (cieniowanie stałą wartością), gdy cały wielokąt jest wypełniony taką samą barwa. | |||
- Cieniowanie Gouroud. | |||
- Cieniowanie Phonga. | |||
Cieniowanie płaskie jest zgodne z rzeczywistością, gdy obserwator lub źródło światła znajduje się w nieskończoności. Może być także stosowane, gdy wielokąt reprezentuje rzeczywiście powierzchnię modelowaną – mamy wtedy do czynienia z rzeczywistą powierzchnią wielościenną. | |||
Jeżeli jednak złożony kształt powierzchni obiektu jest przybliżony wielościanem, to można za pomocą cieniowania wygładzić obiekt niwelując wielościenny charakter. | |||
|} | |} | ||
---- | ---- | ||
| Linia 185: | Linia 236: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd22.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd22.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
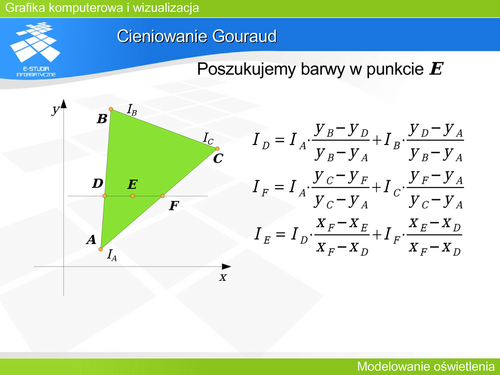
'''Cieniowanie Gouraud''' | |||
Cieniowanie Gouraud jest procesem dwuetapowym: | |||
W pierwszym etapie wyznaczamy (hipotetyczną) barwę w wierzchołkach wielościanu. W tym celu wyznaczamy hipotetyczny wektor normalny jako średnią arytmetyczną wektorów normalnych wszystkich ścian, do których ten wierzchołek należy. Następnie na podstawie wektora normalnego wyznaczamy barwę wierzchołka korzystając z wybranego modelu odbicia światła. | |||
W drugim etapie dokonywana jest liniowa interpolacja barwy zgodnie z zaprezentowanymi wzorami. | |||
|} | |} | ||
---- | ---- | ||
| Linia 191: | Linia 248: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd23.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd23.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
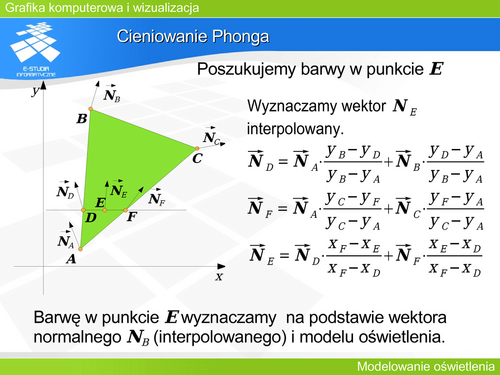
'''Cieniowanie Phonga''' | |||
Cieniowanie Phonga polega na analogicznej interpolacji, tylko że nie barwy ale wektora normalnego. | |||
W pierwszym etapie wyznaczamy wektor normalny w wierzchołku w ten sam sposób jak w cieniowaniu Gouraud. | |||
W drugim etapie wyznaczamy interpolowany wektor normalny dla każdego piksela (to znaczy dla punktu powierzchni odpowiadającego pikselowi). Następnie wyznaczamy barwę piksela, na podstawie interpolowanego wektora normalnego korzystając z wybranego modelu odbicia światła. | |||
|} | |} | ||
---- | ---- | ||
| Linia 197: | Linia 260: | ||
|width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd24.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M8_Slajd24.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
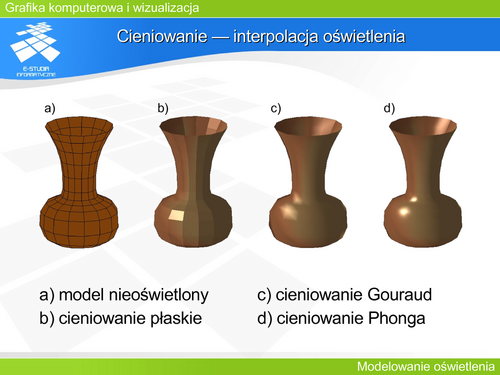
'''Cieniowanie – interpolacja oświetlenia''' | |||
Porównując cieniowanie Gouraud i Phonga można wskazać właściwości każdego z nich. | |||
Obie metody zapewniają ciągłą zmianę barwy eliminując skokowe zmiany cieniowania płaskiego. | |||
Cieniowanie Gouraud nie daje możliwości powstania lokalnego ekstremum (np. rozbłysku światła) w ramach jednego elementu płaskiego. Powoduje to uśrednienie jasności na powierzchni obiektu. Cieniowanie Phonga nie ma tej wady. Interpolacja wektora oddaje poprawnie lokalne ekstrema również w ramach pojedynczego elementu płaskiego. | |||
Cieniowanie Gouraud dopuszcza, niestety, powstawanie pasm Macha. Wady tej jest praktycznie pozbawione cieniowanie Phonga. | |||
Wadą cieniowania Phonga jest fakt, że jest ono ponad dwukrotnie droższe obliczeniowo od cieniowania Gouraud. | |||
|} | |} | ||
---- | ---- | ||
Wersja z 12:31, 27 paź 2006
 |
 |
 |
 |
 |
 |
 |