GKIW Moduł 7

---

---

Problem rozstrzygania widoczności Problem eliminacji elementów zasłoniętych (zwany także problemem rozstrzygania widoczności lub problemem wyznaczania powierzchni widocznych) polega na określeniu, które fragmenty obiektów sceny mogą być widoczne przez wirtualną kamerę (przez obserwatora). Problem wydaje się nam banalny, ale aby w wirtualnym świecie zaszło naturalne dla naszego widzenia zasłanianie jednych obiektów przez drugie, to trzeba to opisać odpowiednim algorytmem. Jest to przykład problemu, dla którego nie jest znane jedno, uniwersalne rozwiązanie. Generalnie rzecz biorąc, zadanie to można traktować jako szeroko rozumiany problem sortowania. Z punkt widzenia obserwatora obiekty leżące dalej są zasłonięte przez obiekty leżące bliżej. Niestety to proste stwierdzenie nie przekłada się na równie prosty algorytm. Już samo określenie „jeden obiekt leżący dalej od drugiego” może prowadzić do niejednoznaczności, gdyż trudno przypisać jedną miarę odległości obiektowi zajmującemu pewien obszar w przestrzeni. Jak więc porównać położenia tych obiektów, a tym bardziej wyciągnąć wnioski o ich wzajemnym zasłanianiu. W skrajnym przypadku można wyobrazić sobie sytuację, że dwa obiekty zasłaniają się w taki sposób, że każdy jest częściowo zasłonięty przez drugi z nich. Do tego relacja częściowego zasłaniania nie jest relacją przechodnią. A zatem wyciągnięcie właściwego wniosku dotyczącego zasłaniania na podstawie wzajemnego położenia obiektów jest zadaniem trudnym. Znanych jest bardzo wiele różnych algorytmów rozstrzygania widoczności. W latach siedemdziesiątych i osiemdziesiątych XX wieku powstało ich rzeczywiście dużo. Warto wspomnieć przynajmniej o kilku z nich.

---

Zasady spójności Sutherland, Sproull i Schumacker zwrócili uwagę na pewną cechę analizy występującą w algorytmach określania widoczności. Jest nią spójność – pewne podobieństwo cech pozwalające wnioskować o zasłanianiu lub widoczności. Jeśli na przykład rozpatrzymy scenę zawierającą wielościany, to o widoczności wierzchołków możemy np. wnioskować na podstawie widoczności ściany.: Jeśli ściana jest widoczna to również jej węzły są widoczne, Tego typu wnioski powinny być ostrożnie formułowane, gdyż nie wszystkie sytuacje są oczywiste (np. wniosek, że odcinek łączący widoczne węzły jest widoczny, nie zawsze jest prawdziwy.

---

---

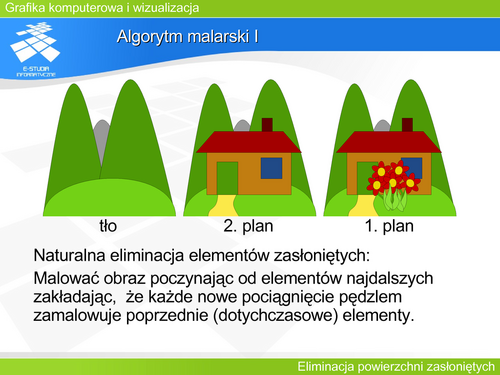
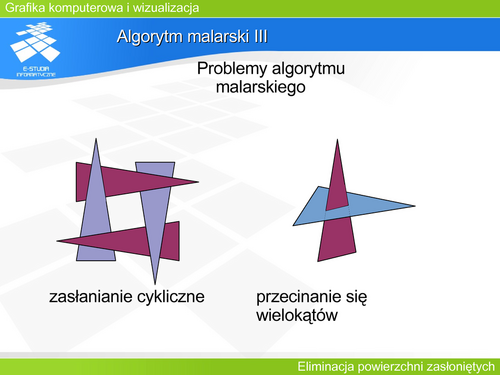
Algorytm malarski I Algorytm malarski (algorytm sortowania ścian) należy do grupy algorytmów z listą priorytetów. Algorytmy te wykorzystują informacje zarówno z przestrzeni obiektu jak i z przestrzeni rzutu (łączą operacje z precyzją obiektową i operacje z precyzją obrazową). Algorytm malarski zaproponowany przez Newella, Newella i Sancha w 1972 roku. Jest jednym z najprostszych opisowo i jednocześnie efektywnym. Polega on na posortowaniu elementarnych fragmentów sceny (wielokątów) zależnie od odległości od obserwatora: od najdalszego do najbliższego. Fragmenty są następnie rysowane w tej kolejności. Zakłada się przy tym, że rysunek powstaje analogicznie do malowania obrazu olejnego (stąd nazwa algorytmu). Tzn. fragment później namalowany zasłania (zamalowuje) wszystko, co było dotychczas namalowane w tym miejscu. Oczywiście tę cechę ma każde urządzenie wyświetlające (monitor, wyświetlacz LCD), ale stosowanie tego algorytmu bezpośrednio na drukarce byłoby niemożliwe.

---

Algorytm malarski II Posortowanie wielokątów jest zadaniem trudnym i może prowadzić do niejednoznaczności. Jeżeli rozpatrzymy dwa wielokąty dowolnie ustawione w przestrzeni, to podstawowym problemem jest ustalenie który z nich jest dalej od obserwatora. To znaczy,. który z nich będzie zasłonięty przez drugi wielokąt z punktu widzenia obserwatora. Żeby to określić stosuje się różne kryteria porównywania położenia. Najprostsze rozwiązanie polega na porównaniu współrzędnych z wielokątów. Jeżeli maksymalna współrzędna z jednego wielokąta jest mniejsza niż minimalna współrzędna z drugiego to pierwszy jest bliżej obserwatora. Oczywiście taki przypadek zachodzi rzadko, najczęściej zakresy współrzędnych wielokątów zazębiają się nie dając możliwości prawidłowego posortowania ich na podstawie takiego kryterium. Lepszym kryterium jest porównanie położenia środków ciężkości wielokątów – bliżej obserwatora znajduje się ten, którego środek ciężkości znajduje się bliżej. Niestety i to kryterium w pewnych sytuacjach zawodzi (czytelnik zechce przeanalizować położenia wielokątów kiedy sortowanie na podstawie położenia środków ciężkości dawałoby niepoprawne rysunki). O wiele lepszym kryterium (chociaż bardziej skomplikowanym obliczeniowo) jest analiza położenia jednego wielokąta względem płaszczyzny wyznaczonej przez drugi wielokąt .Jeżeli pierwszy z nich jest po tej samej stronie płaszczyzny co obserwator, to jest rzeczywiście bliżej obserwatora i nie może być zasłonięty przez drugi wielokąt.

---

Algorytm malarski III Jednak nawet kryterium wykorzystujące analizę położenia względem płaszczyzny nie radzi sobie w szczególnych przypadkach. Należą do nich: zasłanianie cykliczne i przecinanie się wielokątów. Pierwszy z nich stanowi tak naprawdę problem w wielu algorytmach rozstrzygania widoczności. Co prawda w praktyce występuje niezmiernie rzadko, ale dobrze skonstruowany algorytm powinien również w takim przypadku pracować poprawnie. (Przykładem występowania zasłaniania cyklicznego może być przysłona obiektywu fotograficznego, której kolejne elementy zachodzą na siebie.) Oba problemy mogą zostać rozwiązanie przez przecięcie jednego z wielokątów na dwie części i potraktowanie każdej z tych części jako niezależnego wielokąta w przeprowadzanej analizie położenia.

---

Algorytm skaningowy I Algorytm skaningowy (przeglądania liniami poziomymi) jest przykładem algorytmu pracującego w przestrzeni rzutu (działającego z precyzją obrazową). Zasada pracy tego algorytmu oparta jest na założeniu, że w każdym kroku postępowania przeglądana jest jedna linia pozioma obrazu. Można wskazać dwa źródła takiego postępowania. Z jednej strony można bezpośrednio powiązać algorytm z urządzeniem wyświetlającym funkcjonującym na podobnej zasadzie. Przykładem może być monitor, na którym obraz jest powstaje przez generację kolejnych poziomych linii. Z drugiej strony jest to związane z algorytmem wypełniania wielokąta poziomymi liniami. Modyfikując taki algorytm wypełniania można zapewnić dodatkowo eliminację elementów zasłoniętych. Kolejne linie poziome obrazu można rozpatrywać jako przecięcie ekranu i pewnej płaszczyzny prostopadłej do ekranu. Taka płaszczyzna przetnie wszystkie obiekty sceny. Każda linia obrazu może być rozpatrywana niezależnie. Problem rozstrzygania widoczności można zatem uprościć do niezależnej analizy każdej linii, przechodząc z analizy położenia wielokątów w przestrzeni trójwymiarowej do analizy położenia odcinków na płaszczyźnie.

---

Algorytm skaningowy II Najczęściej zakłada się, że wielokąty sceny, które podlegają analizie nie przecinają się – chociaż możliwa jest analiza algorytmem skaningowym również i takich przypadków. Dla danej linii analizuje się tablicę krawędzi (przynależności do wielokąta). Tablica ta określa dla danego piksela do rzutu jakich wielokątów ten piksel należy. Najprościej taką tablicę uzyskać traktując linię przeglądania jako prosta przecinana przez krawędzie kolejnych rzutów wielokątów. Podobnie jak w algorytmie wypełniania istnieje problem krawędzi poziomych. Często zakłada się, że bez zmniejszania ogólności można przyjąć, że taki przypadek nie będzie zachodził. Prościej jednak przeanalizować ten przypadek podobnie jak w wypełnianiu wielokąta liniami poziomymi. Mianowicie przyjąć że odcinek poziomy nie tworzy przecięć z linią przeglądająca ale w całości należy do przecinanego wielokąta (rzutu). Natomiast końce odcinka definiują początek i koniec tej przynależności. Analiza widoczności polega na analizie kolejnych odcinków między punktami przecięć w tablicy krawędzi. Punkty takiego pojedynczego odcinka należą do pewnego zbioru rzutów wielokątów. Jeśli ten zbiór jest pusty, to odcinek ten (tzn. odpowiadające mu piksele urządzenia wyświetlającego) należy wypełnić barwą tła. Jeśli zbiór jest jednoelementowy, to znaczy, że piksele tego odcinka należą dokładnie do jednego rzutu wielokąta. A to oznacza że nie zachodzi żadne zasłanianie i piksele odpowiadające temu odcinkowi należy wypełnić barwą rzutu danego wielokąta. Jeśli zbiór rzutów jest dwu lub więcej elementowy, to do wypełniania należy użyć barwy tego wielokąta, który jest najbliżej obserwatora. Oczywiście w tym przypadku wybór elementu najbliższego jest bardzo prosty, gdyż rozpatrujemy przecięcia wielokątów i płaszczyzny tnącej, czyli zbiór odcinków na płaszczyźnie.

---

Algorytm skaningowy III Algorytm skaningowy był wielokrotnie usprawniany poprzez dodanie mechanizmów przyspieszających jego działanie. Najciekawszą modyfikacją jest uproszczona analiza sąsiednich linii. Można zauważyć, że najczęściej dla sąsiednich linii schemat przynależności kolejnych pikseli do odpowiednich rzutów nie zmienia się. Oznacza to, że można raz zrobić pełną analizę widoczności, a następnie korzystać z niej przy kolejnych liniach przeglądających, dopóki schemat przynależności w tablicy krawędzi się nie zmieni. Złożoność algorytmu jest taka jak sortowania i wynika z pierwszej fazy algorytmu. Modyfikacje usprawniające (takie jak na przykład uproszczona analiza sąsiednich linii) nie wpływają na złożoność asymptotyczną, ale mogą w określonych sytuacjach przyspieszyć działanie algorytmu. Algorytm skaningowy rozwiązuje również problem zasłaniania cyklicznego. Ponieważ w pojedynczym kroku analizujemy jedną linię obrazową czyli jedno przecięcie płaszczyzną tnącą, to zasłanianie cykliczne nie stanowi problemu, gdyż na tej płaszczyźnie nie może zachodzić zasłanianie cykliczne odcinków.

---

Algorytm podziału binarnego I Pomysł wykorzystania zorientowania ścian pochodzący z 1969 roku został zastosowany w latach 1980-1983 do budowy algorytmu rozstrzygania widoczności zwanego algorytmem drzewa binarnego podziału przestrzeni (ang. BSP tree). Rozpatrzmy przypadek jak na rysunku. Każdej płaszczyźnie można przypisać zorientowanie (zaznaczone strzałkami, zwrot zgodny ze strzałkami w drzewie został zaznaczony + , zwrot przeciwny został oznaczony - ). Kolejność analizy (budowy drzewa podziału) – to znaczy wybór kolejnych płaszczyzn jest dowolny. Może to oczywiście wpłynąć na kształt drzewa, wpływa także na konieczność podziału ścian wielościanu. Na przykład ściana c na rysunku została podzielona na fragmenty c1, c2 i c3 co wynika z wcześniejszego podziału przestrzeni. Algorytm podziału binarnego w takiej postaci może zostać także wykorzystany do sprawdzenia czy dany punkt należy do wnętrza wielościanu.

---

Algorytm podziału binarnego II Drzewo jest przeglądane w kolejności INORDER z uwzględnieniem zorientowania. procedure przeglądaj_BSP (drzewo) begin if drzewo jest niepuste then if obserwator „z przodu” (+) korzenia drzewa then begin przeglądaj_BSP (tylne (-) poddrzewo); narysuj obiekt z korzenia drzewa; przeglądaj_BSP (przednie (+) poddrzewo); end; else // tu obserwator z tyłu (-) korzenia drzewa begin przeglądaj_BSP (przednie (+) poddrzewo); narysuj obiekt z korzenia drzewa; przeglądaj_BSP (tylne (-) poddrzewo); end; end;

---

Zorientowanie ściany I Rozpatrzmy przypadek wielościanu wypukłego. Jest to jeden z przykładów problemu eliminacji elementów zasłoniętych, dla którego można pokazać kilka efektywnych i jednocześnie prostych algorytmów. Można zauważyć, że jeżeli na scenie jest dowolny wielościan wypukły (ale tylko jeden !), to wnioskowanie o widoczności jego elementów jest dość proste. Traktując taką scenę jako zbiór wielokątów (z których każdy jest oczywiście ścianą wielościanu), można ten zbiór podzielić na trzy grupy: 1. Wielokąty widoczne przez obserwatora (wielokąty przednie). 2. Wielokąty niewidoczne – zasłonięte (wielokąty tylne). 3. Wielokąty, których rzut jest odcinkiem. Wielokąty ostatniej grupy są pomijalne, odpowiednie odcinki zostaną i tak narysowane jeśli pojawią się wielokąty widoczne. W pierwszej i drugiej grupie występują wielokąty, które w całości podlegają określonym zasadom widoczności i przynależności do grupy. Nie może zachodzić przypadek, że tylko część wielokąta jest widoczna (a druga część zasłonięta). A zatem rozwiązanie zadania wybór elementów widocznych w przypadku wielościanu wypukłego sprowadza się do określenia zbioru wielokątów należących do pierwszej grupy. I one powinny być (w całości) narysowane. Można pokazać trzy (co najmniej) różne sposoby rozwiązanie tak zdefiniowanego zdania. Pierwszy sposób (Rozwiązanie A) polega na analizie położenia obiektów w przestrzeni. Definiowane są określone wektory a następnie jest wyznaczany iloczyn skalarny tych wektorów. Znak tego iloczynu określa przynależność do określonej grupy. Zwróćmy uwagę na fakt, że w tym przypadku nie ma w ogóle mowy o jakimkolwiek rzucie. Położenie obserwatora w przestrzeni w zupełności wystarczy.

---

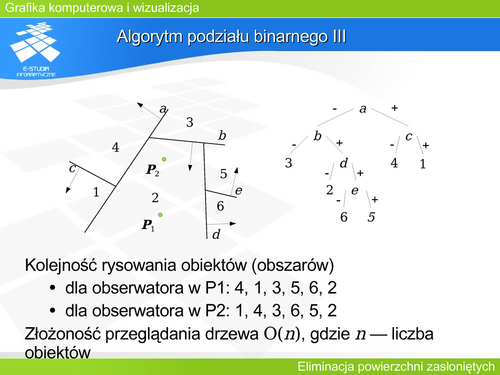
Algorytm podziału binarnego III W warunkach rzeczywistej analizy sceny przy wyborze płaszczyzn podziału warto posługiwać się płaszczyznami związanymi bezpośrednio z obiektami (zawierającymi na przykład ściany). Przykład przekroju sceny i odpowiadające mu drzewo podziału prezentuje rysunek. Zakładamy dla uproszczenia, że w każdym obszarze (ponumerowanym) znajduje się jeden obiekt. Stosując algorytm binarnego podziału należy wyznaczyć kolejność rysowania, w taki sposób, aby z punktu widzenia obserwatora rysować obiekty od najdalszych do najbliższych (najpierw zasłaniane potem zasłaniające). Drzewo uwzględnia wszystkie ściany i pozwala wskazać kolejność zasłaniania po przejściu zaproponowanym algorytmem drzewa. Oczywiście drzewo nie uwzględnia położenia obserwatora, natomiast położenie to wpływa na drogę przejścia przez drzewo. Rysunek pokazuje różne kolejności rysowania obiektów dla dwóch różnych położeń obserwatora. Ciekawym przypadkiem jest sytuacja, gdy obserwator znajduje się wewnątrz obszaru. Wtedy drzewo binarnego podziału pokazuje właściwą kolejność bez względu na kierunek patrzenia obserwatora ! Algorytm drzewa binarnego podziału przestrzeni był bardzo długo traktowany jako niezwykle elegancka ciekawostka, ze względu na skomplikowanie tworzenia drzewa podziału. Dopiero silny rozwój gier komputerowych w latach 90 dwudziestego wieku spowodował, że algorytm ten przeżywa swój renesans. Zauważono bowiem, że warto na użytek gier rozdzielić etap tworzenia drzewa od etapu przeglądania. Jeśli przyjmiemy, że w każdym elemencie podziału znajduje się jeden obiekt sceny, to samo przeglądanie algorytmem INORDER± ma złożoność liniową ze względu na liczbę obiektów i to niezależnie od zbalansowania drzewa. Drzewo zostaje zatem utworzone przez twórców gry w momencie generowania „mapy” gry. Natomiast przeglądane jest w momencie realizacji (wirtualnego poruszania się gracza/bohatera po świecie gry). Co więcej, sprawę można dodatkowo uprościć dzieląc mapę na obszary, w których jest ustalona kolejność rysowania obiektów, a następnie zapisać gotowe schematy kolejności dla poszczególnych obszarów. W tym przypadku podczas realizacji gry nawet przeglądanie drzewa nie jest potrzebne. Warto dodać, że w latach 1992-1995 (Teller, Luebke, Georges) powstała metoda wyboru potencjalnych elementów widocznych (ang.PVS – Potentially Visible Set) pozwalająca określić przybliżony zakres widoczności obiektów. Metoda ta jest często łączona z generacją drzewa BSP.

---

Algorytm bufora głębokości I Algorytm bufora głębokości (Z-bufora) został zaproponowany przez Catmulla w 1974 roku. Jest jednym z najprostszych w implementacji algorytmów rozstrzygania widoczności. Zakłada istnienie bufora o rozmiarze całego wyświetlanego obszaru (ekranu) – występuje w tym przypadku odpowiedniość pozycji piksela ekranu i odpowiadającej mu pozycji w buforze. Dla każdego piksela w buforze zapamiętywana jest odpowiadająca mu głębokość czyli współrzędna zp. Na początku pracy algorytmu bufor Z jest wypełniany maksymalną wartością współrzędnej z, jaka może wystąpić w analizowanym obszarze. Jednocześnie wszystkie piksele obrazu przyjmują barwę tła. Następnie rysowane są wielokąty (w dowolnej kolejności) – to znaczy wypełniane są ich rzuty odpowiednią barwą. Podczas wypełniania zwykła procedura wypełniająca jest poszerzona o sprawdzenie głębokości odpowiadającej danemu pikselowi. Piksel jest wypełniony tylko wtedy, kiedy jego z jest mniejsze niż wartość zapisana w buforze. Mechanizm ten powoduje, że podczas wypełniania kolejnych wielokątów szukany jest piksel, którego współrzędna z jest najmniejsza – to znaczy szukany jest punkt leżący najbliżej obserwatora – czyli punkt rzeczywiście widoczny.

---

Algorytm bufora głębokości II Algorytm bufora głębokości rozstrzyga widoczność dla dowolnych scen wielościennych, jest niewrażliwy na zasłanianie cykliczne ani przecinanie obiektów. Nie wymaga żadnych dodatkowych struktur danych ani operacji wstępnych. Dodatkowo, biorąc pod uwagę fakt, że wielokąty są obiektami płaskimi można wyznaczyć proste zależności przyrostowe wiążąc kolejne zmiany współrzędnych z wypełnianiem wielokąta liniami. Powoduje to, że dodatkowy czas potrzebny na rozszerzenie algorytmu wypełniania o rozstrzyganie widoczności jest niewielki. Przyjmuje się, że jest to algorytm o złożoności liniowej ze względu na liczbę wielokątów, ale dla ich dużej liczby czas rozstrzygania widoczności staje się w przybliżeniu praktycznie niezależny od liczby wielokątów w danej bryle widzenia. Algorytm ma tylko jedną wadą – potrzebuje pamięci o rozmiarze obrazu pozwalającej zapisać odległość dla każdego piksela. Jeszcze do niedawna (koniec dwudziestego wieku) był to warunek trudny do spełnienia. Realizacja algorytmu wymagała dodatkowo wykonania podziału obrazu na fragmenty, które mogły być razem z odpowiadającym mu buforem zmieszczone do pamięci. Dzisiaj nie stanowi to żadnego problemu. Prostota algorytmu sprzyja również implementacji sprzętowej. Stacje graficzne i większość dobrych kart graficznych ma dzisiaj możliwość sprzętowej realizacji bufora głębokości.

---

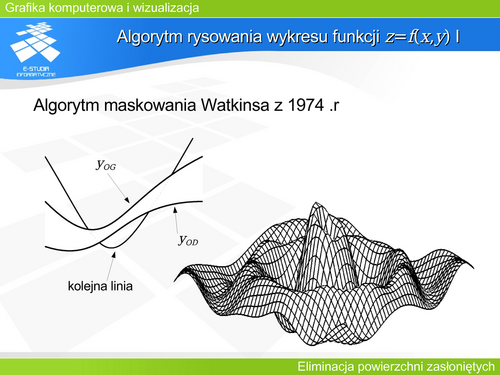
Algorytm rysowania wykresu funkcji z=f(x,y) I Zadanie rysowania powierzchni będącej wykresem funkcji dwóch zmiennych jest jednym z częściej realizowanych zadań grafiki prezentacyjnej. Dodatkowo można zauważyć, że jest to dobry sposób uproszczonego rysowania rzeźby terenu. Powierzchnia będąca wykresem funkcji z=f(x,y) należy do szczególnej klasy obiektów trójwymiarowych, dla której można pokazać uproszczony algorytm rozstrzygania widoczności. Można przyjąć, że dziedziną D funkcji dla rozpatrywanego fragmentu powierzchni jest prostokątem [xmin,xmax] x [ymin,ymax]. Jeśli dziedzinę D podzielimy równomierną siatką za pomocą linii równoległych odpowiednio do osi x i osi y, to punkt [xi,yj] będzie węzłem takiej siatki (dla 1  i  NX oraz 1  j  NY, gdzie NX, NY określają liczbę linii siatki dla każdej współrzędnej). Punkt [zij,xi,yj] dla zij=f(xi,yj) jest węzłem siatki rozpiętej na powierzchni będącej wykresem punkcji. Taki przykład najczęściej występuje w zastosowaniach praktycznych, gdzie wartości węzłowe pochodzą na przykład z pomiarów lub symulacji. Przybliżoną powierzchnię rysujemy łącząc węzły odcinkami. Watkins w 1974 roku zaproponował algorytm maskowania pozwalający rysować kolejne krzywe (łamane) siatki rozpiętej na powierzchni będącej wykresem funkcji. Można zauważyć dotychczas narysowany fragment (pierwszym takim fragmentem jest obszar powierzchni pomiędzy pierwszymi dwoma krzywymi/łamanymi) może zasłaniać wszystkie później rysowane elementy powierzchni. A zatem do realizacji algorytmu wystarczy zdefiniować bufor górny (ograniczenie górne YOG we współrzędnych rzutu) i bufor dolny (ograniczenie dolne YOD we współrzędnych rzutu), a następnie w każdym kroku sprawdzać położenie rysowanego elementu (odcinka) względem buforów. Jeśli element jest powyżej ograniczenia górnego lub poniżej dolnego to jest rysowany, w przeciwnym przypadku (między ograniczeniami) to nie jest rysowany. Oczywiście każdy narysowany element powiększa (rozszerza w danym kierunku) odpowiednie ograniczenie.

---

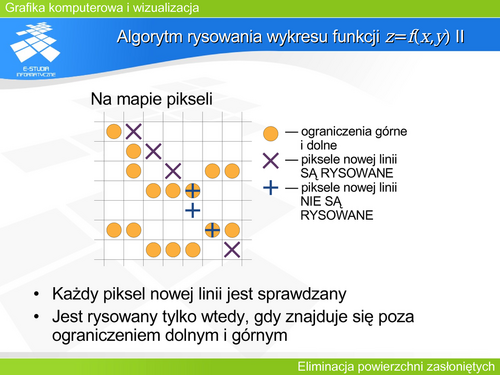
Algorytm rysowania wykresu funkcji z=f(x,y) II Standardowe podejście w algorytmie maskowania Watkinsa wymaga podczas rysowania analizy położenia odcinka względem łamanej (górnego ograniczenia lub dolnego). Tego typu zadanie jest klasycznym zadaniem geometrii obliczeniowej i nie należy do najprostszych – wymagałoby dodatkowego, znaczącego czasu realizacji. Można zmodyfikować problem tak, aby nie było to w ogóle konieczne. W tym celu rozpatrzmy tę samą sytuację ale na mapie pikseli. Ograniczenia górne i dolne w tym przypadku odpowiadają zestawowi pikseli, które w kolejnych kolumnach określają minimalną i maksymalną wysokość. Rysując każdy nowy piksel wystarczy sprawdzić jego położenie względem tego minimum lub maksimum. A to jest operacją bardzo prosta. Jeśli nowy piksel jest powyżej maksimum (lub poniżej minimum) to jest rysowany, jeśli pomiędzy minimum i maksimum to rysowany nie jest. Oczywiście rysowany piksel przesuwa odpowiednie maksimum (lub minimum).

---

Algorytm rysowania wykresu funkcji z=f(x,y) III Zaproponowany mechanizm maskowania dla mapy pikseli może zostać połączony z algorytmem Bresenhama rysowania odcinka. Tak zmodyfikowany algorytm będzie rysował odcinki z uwzględnieniem rozstrzygania widoczności dla siatki rozpiętej na powierzchni będącej wykresem funkcji dwóch zmiennych. Można pokazać że modyfikacja algorytmu Bresenhama wymaga dodania jednej instrukcji porównania i jednej instrukcji podstawienia. Nie zmienia to znacząco czasu realizacji rysowania odcinków. Dodatkowo należy zwrócić uwagę na kolejność wyboru do rysowania odcinków siatki. Jeśli byłyby one rysowane w naturalnej kolejności związanej z rodzinami linii dla stałego x, i dla stałego y, to mogłyby wystąpić problemy z wzajemnym zasłanianiem. Dobrym rozwiązaniem jest kolejność typu ZIG-ZAG (tzn. odcinki na przemian z każdej rodziny) lub kolejność zaproponowana na rysunku. Warto dodatkowo zwrócić uwagę na fakt, że taka wersja algorytmu poprawnie pracuje tylko dla rzutu równoległego wykresu funkcji. Analiza rysowania na mapie pikseli z uwzględnieniem minimum i maksimum kolumny pokazuje, że dla odcinków rysowanych w rzucie perspektywicznym wystąpią błędy.

---

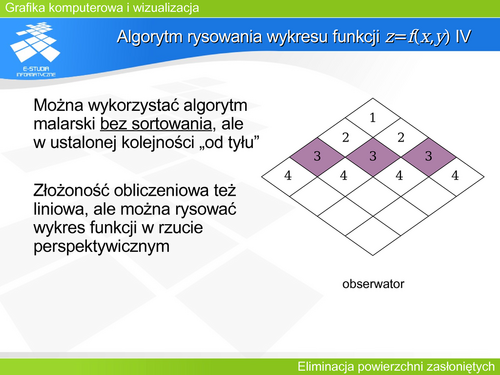
Algorytm rysowania wykresu funkcji z=f(x,y) IV Inną możliwością rysowania powierzchni wykresu funkcji jest zastosowanie algorytmu malarskiego. Oczywiście wykres funkcji pozwala zrezygnować sortowania koniecznego w algorytmie malarskim. W tym przypadku wystarczy uwzględnić kolejność wynikającą z odległości „oczek” siatki dziedziny funkcji od obserwatora. Na rysunku oczka o tym samym numerze mogą być rysowane w dowolnej kolejności – nie mogą się wzajemnie zasłaniać. Zastosowanie algorytmu malarskiego ma dodatkową zaletę: algorytm ten poprawnie rysuje powierzchnię będącą wykresem funkcji także dla rzutu perspektywicznego. Algorytm rysowania powierzchni będącej wykresem funkcji dwóch zmiennych jest przykładem algorytmu rozstrzygania widoczności dla szczególnej klasy obiektów trójwymiarowych. Drugim przykładem tego typu zadania jest algorytm rysowania figur obrotowych. Szczegóły tego algorytmu czytelnik może znaleźć w książce M.Jankowskiego Elementy grafiki komputerowej.

---

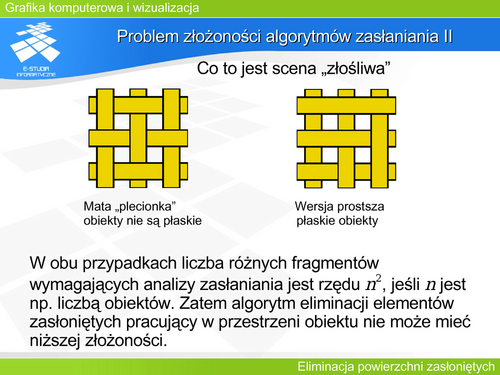
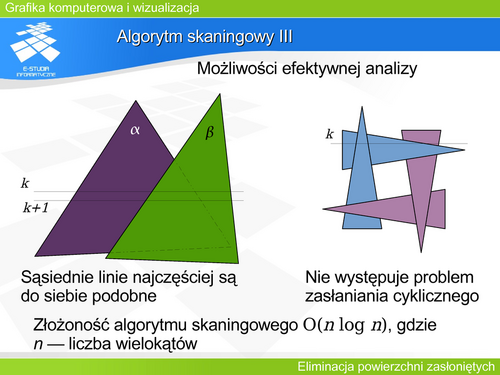
Problem złożoności algorytmów zasłaniania I Twórcy algorytmów rozstrzygania widoczności starali się zawsze obniżyć złożoność obliczeniową tych algorytmów. Wielokrotnie były przeprowadzane analizy złożoności algorytmów zasłaniania. Pokazują one, że nawet najtrudniejsze przypadki mogą zostać rozwiązane ze złożonością kwadratową. Z drugiej strony można się zastanawiać nad minimalna liczbą operacji, niezbędnych do rozwiązania problemu zasłaniania. W większości przypadków wyrafinowane algorytmy wyznaczają elementy zasłonięte ze złożonością O(nlogn), gdzie n jest miarą złożoności sceny (liczbą wielokątów lub krawędzi). Dla algorytmów pracujących w przestrzeni rzutu (z precyzją obrazową) złożoność będzie liniowa.

---

Problem złożoności algorytmów zasłaniania II Można pokazać, że dla wybranych scen minimalna złożoność algorytmów pracujących w przestrzeni obiektu musi być rzędu kwadratowego. Wynika to z budowy sceny. Wyrafinowane algorytmy mogą w tym przypadku dać rozwiązanie gorsze niż kwadratowe.

---

---

Zorientowanie ściany II Rozwiązanie B korzysta z informacji zarówno pochodzących z przestrzeni obiektu (sceny), jak i z informacji jakie dostarcza rzut. – Porównywane jest zorientowanie ściany obiektu (w przestrzeni obiektu) i zorientowanie rzutu ściany (w przestrzeni rzutu). Jeśli oba zorientowania są jednakowe, to ściana jest widoczna (przednia).

---

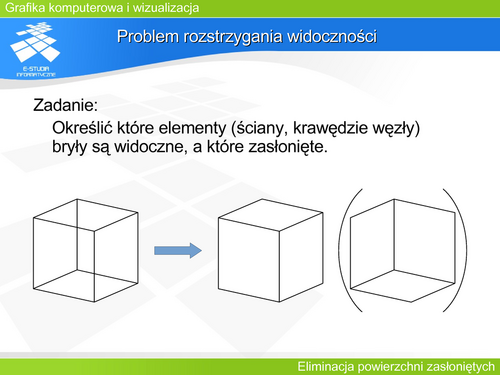
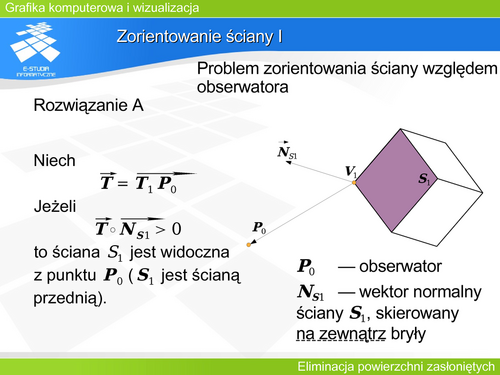
Bryła wypukła I Zadanie określenia widoczności elementów wielościanu wypukłego można więc rozwiązać na dwa sposoby korzystając z rozwiązań A i B sprawdzających zorientowanie poszczególnych ścian.

---

Bryła wypukła II Analizę widoczności w przypadku wielościanu wypukłego, można przeprowadzić opierając się tylko na informacji z przestrzeni rzutu – sposób C. W tym celu należy podzielić wierzchołki rzutu na dwa typy. Pierwszy typ charakteryzuje się tym, że węzeł oraz zewnętrzne krawędzie są widoczne. O pozostałych krawędziach i ich widoczności nie można nic powiedzieć. Drugi typ charakteryzuje się tym , że co prawda nie można stwierdzić czy węzeł jest widoczny czy nie, ale za to wszystkie elementy mają taki sam atrybut. A więc jeśli jakaś jedna krawędź jest widoczna, to cały węzeł i wszystkie jego krawędzie są widoczne.

---

Bryła wypukła III Korzystając z klasyfikacji węzłów można zaproponować sposób C wyznaczania widoczności elementów wielościanu wypukłego. Określając widoczność jednego węzła drugiego typu można przenieść ten sam atrybut widoczności do sąsiednich węzłów, przechodząc od jednego węzła do drugiego. W ten sposób powstają dwa komplementarne obrazy. W takim postępowaniu nie jest potrzebna informacja z przestrzeni obiektu. Wystarczy tylko informacja dotycząca rzutu.

---

Klasy algorytmów Trzy sposoby rozwiązania problemu widoczności pokazują trzy sposoby wykorzystania informacji, pochodzących albo z przestrzeni obiektu (sceny), albo przestrzeni rzutu, albo obu. Oczywiście o ile w przypadku wielościanu wypukłego ten podział jest bardzo ostry i jednoznaczny, o tyle w przypadku dowolnego innego algorytmu podział będzie zdecydowanie mniej ostry i będzie oznaczał, że dany algorytm w większym stopniu wykorzystuje informację z jednej lub drugiej przestrzeni. Z drugiej strony często mówi się o precyzji obrazowej lub obiektowej danego algorytmu. Oznacza to, że algorytmy pracujące z precyzją obrazowa wykonują obliczenia z dokładnością urządzenia wyświetlającego (wynikającą z wyświetlania pojedynczego piksela). Algorytmy pracujące z precyzją obiektowa wykonują obliczenia z dokładnością związaną z definicją obiektów, a nie pikseli.

---

Bryła wypukła, złożoność algorytmów Aby określić złożoność algorytmów określania widoczności należy zdefiniować miarę złożoności sceny (obiektu). Najczęściej przyjmuje się, liczbę ścian jako taką miarę. Złożoność trzech wariantów algorytmów eliminacji elementów zasłoniętych dla wielościanu wypukłego jest liniowa. Jest to szczególny przypadek wśród algorytmów określania widoczności.

---

Bryła dowolna W przypadku bryły dowolnej lub zestawu dowolnych brył, podział ścian na przednie i tylne nie wystarczy, gdyż taka analiza nie uwzględnia wzajemnego zasłaniania ścian, jakie może wystąpić między obiektami lub ścianami tego samego obiektu. Problem taki występuje także dla zestawu brył wypukłych, tylko dla jednej bryły wypukłej można pokazać prostszy algorytm. Naturalnym podejściem jest analiza wzajemnego położenia ścian, ale w takim przypadku trzeba przeanalizować wszystkie pary ścian (analiza „każdy z każdym”). Prowadzi to oczywiście do kwadratowej złożoności obliczeniowej algorytmu. Najprostszym mechanizmem przyspieszającym takie postępowanie jest test MINMAX czyli „opakowanie” wielokątów prostopadłościanami definiującymi minimum i maksimum po każdej współrzędnej dla danego wielokąta. Porównując wzajemne położenie prostopadłościanów opakowujących (co jest prostsze gdyż jest porównaniem minimów i maksimów współrzędnych) można wyeliminować wiele przypadków, gdy wielościany nie mogą się zasłaniać. Oczywiście takie postępowanie nie zmienia asymptotycznej złożoności obliczeniowej. Test MINMAX jest często stosowany do różnych algorytmów eliminacji elementów zasłoniętych. Pierwszy algorytm rozstrzygania widoczności dla dowolnych brył, przy założeniu że ściany są trójkątami (a przecież dowolny wielokąt zawsze może zostać rozłożony na zbiór trójkątów) podał Ricci w 1972 roku. Był to algorytm pracujący metodą „każdy z każdym” o kwadratowej złożoności obliczeniowej.

---