MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 185: | Linia 185: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd23.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd23.png|thumb|500px]] | ||
|valign="top"|Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek d jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający mniejszą niż w punkcie bieżącym wartość funkcji celu. | |valign="top"|Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek <math>d</math> jest kierunkiem poprawy. Mając '''ustalony kierunek poprawy''' powinniśmy poruszając się wzdłuż niego '''znaleźć punkt dający mniejszą''' niż w punkcie bieżącym '''wartość funkcji celu'''. | ||
|} | |} | ||
---- | ---- | ||
| Linia 197: | Linia 197: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd25.png|thumb|500px]] | ||
|valign="top"|Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu <math>\bar{x} \in P(x^{(k)};d)\subset R^n</math> jest równoważne ustaleniu pewnego <math>\bar{\alpha} \in R</math> Zatem zmieniając <math>\alpha </math> od zera do plus nieskończoności ruszamy się wzdłuż prostej <math>P(x^{(k)};d)</math> w kierunku malenia funkcji celu. Konkretną wartość <math>\bar{\alpha}</math> – długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze P(x(k);d) trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: wybieramy duży krok początkowy <math>\alpha ^{(0)}</math>, gdy <math>f(x^{(k)}+\alpha ^{(0)}d)<f(x^{(k)})</math> to <math>\alpha^{(0)}</math> uznajemy za długość kroku, gdy przeciwnie – zmniejszamy <math>\alpha^{(0)}</math> do <math>\alpha^{(1)}</math>), powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę | |valign="top"|Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu <math>\bar{x} \in P(x^{(k)};d)\subset \mathbb{R}^n</math> jest równoważne ustaleniu pewnego <math>\bar{\alpha} \in \mathbb{R}</math>. Zatem '''zmieniając''' <math>\alpha</math> '''od zera do plus nieskończoności''' ruszamy się wzdłuż prostej <math>P(x^{(k)};d)</math> w kierunku malenia funkcji celu. Konkretną wartość <math>\bar{\alpha}</math> – '''długość kroku''' – możemy ustalić ''a priori''. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze <math>P(x^{(k)};d)</math> trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: | ||
wybieramy duży krok początkowy <math>\alpha ^{(0)}</math>, | |||
gdy <math>f(x^{(k)}+\alpha ^{(0)}d)<f(x^{(k)})</math> to <math>\alpha^{(0)}</math> uznajemy za długość kroku, | |||
gdy przeciwnie – zmniejszamy <math>\alpha^{(0)}</math> do <math>\alpha^{(1)}</math>), | |||
powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę. | |||
|} | |} | ||
---- | ---- | ||
| Linia 203: | Linia 211: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd26.png|thumb|500px]] | ||
|valign="top"|Dokonujemy, jak mówimy '''minimalizacji w kierunku'''. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha</math> (<math>x^{(k)}</math> i <math>d</math> są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x | |valign="top"|Dokonujemy, jak mówimy '''minimalizacji w kierunku'''. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej <math>\alpha</math> (<math>x^{(k)}</math> i <math>d</math> są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny <math>P(x^{(k)};d)</math> jest określony jednym ograniczeniem równościowym. | ||
Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu. | ||
| Linia 229: | Linia 237: | ||
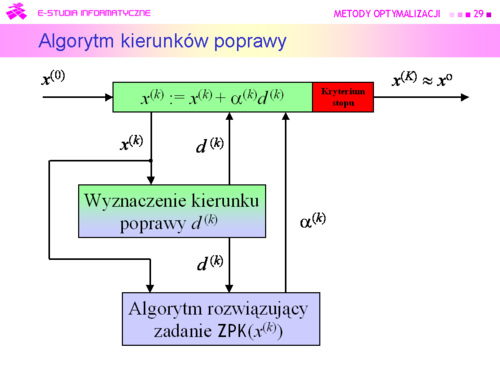
Inicjalizacja | Inicjalizacja | ||
Wybierz punkt początkowy <math>x^{(0)}</math>. | Wybierz punkt początkowy <math>x^{(0)}</math>. | ||
Podstaw k := 0. | Podstaw <math>k := 0</math>. | ||
Kroki algorytmu | Kroki algorytmu | ||
#Dla punktu <math>x^{(k)}</math> wyznacz kierunek poprawy <math>d^{(k)}</math>. | #Dla punktu <math>x^{(k)}</math> wyznacz kierunek poprawy <math>d^{(k)}</math>. | ||
#Ustal długość kroku w kierunku poprawy <math>\alpha ^{(k)}</math> | #Ustal długość kroku w kierunku poprawy <math>\alpha ^{(k)}</math>. | ||
#Wylicz następny punkt podstawiając <math>x^{(k)}:=x^{(k)}+\alpha ^{(k)}d^{(k)}</math>. | #Wylicz następny punkt podstawiając <math>x^{(k)}:=x^{(k)}+\alpha ^{(k)}d^{(k)}</math>. | ||
#Jeżeli spełnione jest kryterium (test) stopu, to <math>x^{(k)}</math> przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 5. | #Jeżeli spełnione jest kryterium (test) stopu, to <math>x^{(k)}</math> przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 5. | ||
#Podstaw k := k + 1, idź do 1. | #Podstaw <math>k := k + 1</math>, idź do 1. | ||
|} | |} | ||
| Linia 273: | Linia 281: | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*'''Zbieżność skończona''', która ma miejsce wtedy gdy istnieje taka liczba <math>K</math> dla której <math>x^{(K)} = x^o</math>. Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm | *'''Zbieżność skończona''', która ma miejsce wtedy gdy istnieje taka liczba <math>K</math> dla której <math>x^{(K)} = x^o</math>. Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm SIMPLEX rozwiązywania zadań liniowych. Jednak jak pamiętamy, liczba iteracji może być bardzo duża, co oznacza, że na rozwiązanie zadania trzeba bardzo długo czekać. Metody punktu wewnętrznego nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod tego typu. A wniosek ogólny – z praktycznego punktu widzenia zbieżność skończona z bardzo dużym <math>K</math> może być gorsza niż zbieżność nieskończona, w sytuacji w której ciąg szybko zmierza do niewielkiego otoczenia rozwiązania. | ||
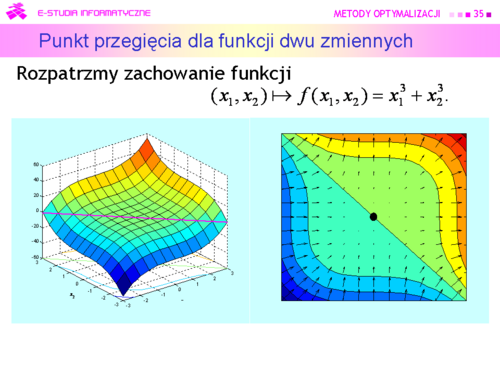
*Znana Państwu z analizy matematycznej '''zbieżność wektorowego ciągu nieskończonego''', zwana jest w teorii metod optymalizacji krótko '''zbieżnością''' (nieskończoną). Jest ona rozumiana dwojako: jako '''zbieżność do rozwiązania''' <math>x^o</math>, albo dla funkcji gładkich – '''zbieżność do punktu stacjonarnego gradientu''', tzn. takiego wektora <math>\hat{x}</math>, że <math>\nabla f (\hat{x})=0</math>. Jak pamiętamy punkt <math>\hat{x}</math> może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie. | *Znana Państwu z analizy matematycznej '''zbieżność wektorowego ciągu nieskończonego''', zwana jest w teorii metod optymalizacji krótko '''zbieżnością''' (nieskończoną). Jest ona rozumiana dwojako: jako '''zbieżność do rozwiązania''' <math>x^o</math>, albo dla funkcji gładkich – '''zbieżność do punktu stacjonarnego gradientu''', tzn. takiego wektora <math>\hat{x}</math>, że <math>\nabla f (\hat{x})=0</math>. Jak pamiętamy punkt <math>\hat{x}</math> może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie. | ||
*Dlatego w niektórych wypadkach twórcom algorytmów udaje się udowodnić własność jeszcze słabszą: '''ciąg''' wektorów generowany przez algorytm '''zawiera podciąg zbieżny'''. Akceptacja zbieżności tego rodzaju po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym “optymistycznym” podejściu do analizy sytuacji. | *Dlatego w niektórych wypadkach twórcom algorytmów udaje się udowodnić własność jeszcze słabszą: '''ciąg''' wektorów generowany przez algorytm '''zawiera podciąg zbieżny'''. Akceptacja zbieżności tego rodzaju po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym “optymistycznym” podejściu do analizy sytuacji. | ||
| Linia 327: | Linia 335: | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd38.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd38.png|thumb|500px]] | ||
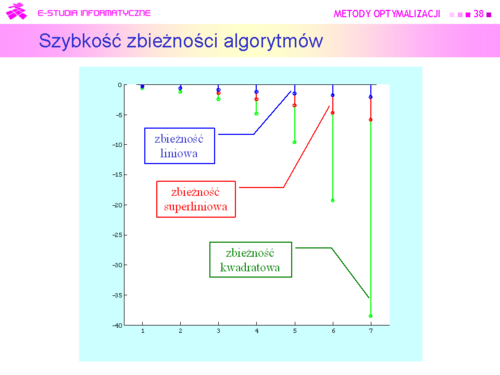
|valign="top"|Na rysunku przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów. | |valign="top"|Na rysunku przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów. | ||
Widać że zbieżność liniowa jest najwolniejsza, a kwadratowa najszybsza. Różne eksperymenty pokazały, że w zastosowaniach praktycznych szybkość liniowa jest do zaakceptowania gdy granica <math>\rho </math> jest dostatecznie mała, nie większa niż <math>\frac{1}{4}</math>. | Widać że '''zbieżność liniowa jest najwolniejsza''', a '''kwadratowa - najszybsza'''. Różne eksperymenty pokazały, że w zastosowaniach praktycznych '''szybkość liniowa''' jest '''do zaakceptowania gdy granica <math>\rho </math>''' jest dostatecznie mała, '''nie większa niż <math>\frac{1}{4}</math>'''. | ||
|} | |} | ||
| Linia 340: | Linia 348: | ||
{| border="0" cellpadding="4" width="125%" | {| border="0" cellpadding="4" width="125%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd40.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd40.png|thumb|500px]] | ||
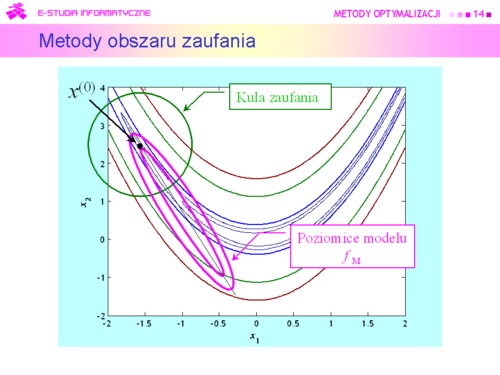
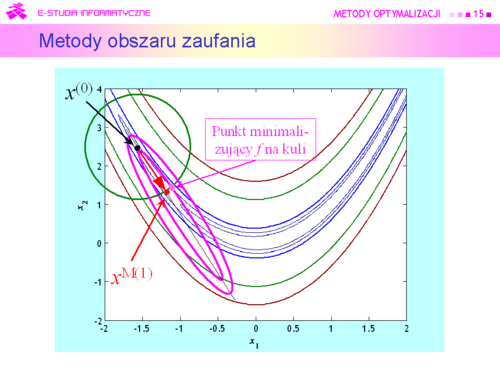
|valign="top"|Pierwszy sposób został omówiony dokładnie w wykładzie poprzednim. Została pokazana ograniczoność możliwości jego stosowania. Ogólna zasada działania pozostałych trzech schematów jest taka sama i polega na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę (np. minimalizującego odpowiednio dobraną funkcję). W metodzie obszarów zaufania to zadanie poprawy jest wielowymiarową minimalizacją przy ograniczeniach, najczęściej funkcji kwadratowej. Dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej. Schematy te zostały przedstawione ogólnie i dla zastosowań praktycznych wymagają „doprecyzowania”. Zostanie to uczynione w następnych wykładach. | |valign="top"|'''Pierwszy sposób''' został omówiony dokładnie w wykładzie poprzednim. Została pokazana '''ograniczoność możliwości''' jego '''stosowania'''. Ogólna zasada działania pozostałych trzech schematów jest taka sama i polega na naprzemiennym rozwiązywaniu dwu zadań: '''generacji zbioru podlegającego przeszukaniu''' i '''szukaniu w tym zbiorze punktu dającego poprawę''' (np. minimalizującego odpowiednio dobraną funkcję). W metodzie obszarów zaufania to '''zadanie poprawy''' jest wielowymiarową minimalizacją przy ograniczeniach, najczęściej funkcji kwadratowej. Dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej. Schematy te zostały przedstawione ogólnie i dla zastosowań praktycznych wymagają „doprecyzowania”. Zostanie to uczynione w następnych wykładach. | ||
|} | |} | ||
---- | ---- | ||
Wersja z 10:46, 6 paź 2006
 |
 |
 |
 |
 |
Algorytm może być:
a następnie przeszukiwać je tak jak poprzednio. |
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
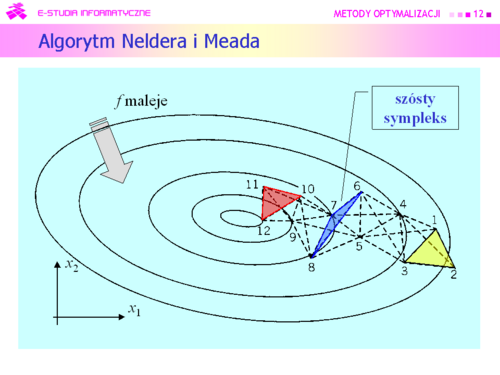 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
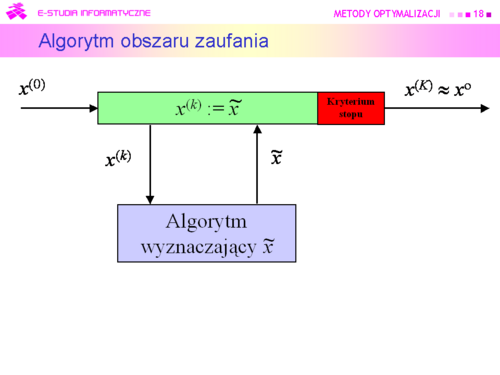
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
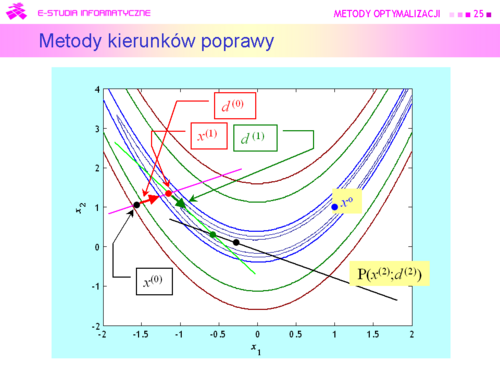
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbę iteracji. |
 |
 |
 |
 |
 |
 |