MO Moduł 5

---

---

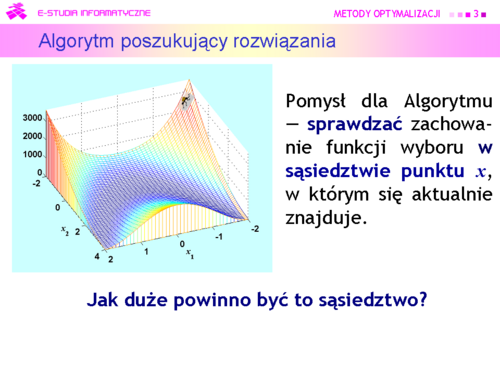
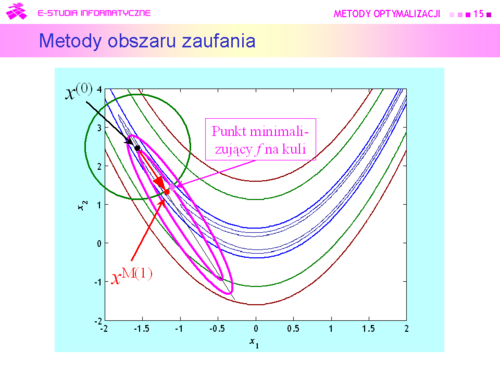
Powróćmy do naszych rozważań z części drugiej wykładu trzeciego. Jak pamiętamy, Algorytm jest ślepy — nie może zobaczyć rzeźby trenu na którym się znajduje. Na schodach szedł w prawo, potem w lewo — sprawdzał swoje otoczenie. Teraz otoczenie ma więcej wymiarów, ale pomysł może być ten sam — sprawdzać zachowanie funkcji wyboru w sąsiedztwie punktu $x$, w którym się aktualnie znajduje. Natychmiast pojawia się pytanie — jak duże powinno być to sąsiedztwo? Udzielenie przemyślanej odpowiedzi nie jest zagadnieniem łatwym, ponieważ wielkość przeszukiwanego obszaru ma, intuicyjnie, wpływ, z jednej strony na szybkość znalezienia ekstremum mierzoną ilością sprawdzanych obszarów (im większy tym szybciej), a z drugiej na dokładność Algorytmu (przy ograniczonych możliwościach przeszukiwania — im mniejszy tym dokładniej).

---

---

---

Przeanalizujmy teraz sposób pierwszy, zakładający kompletną niewiedzę o kształcie funkcji wyboru. Oznacza to że z punktów kuli, zaczepionej w „bieżącym” punkcie $x^{(k)}$ Algorytm musi wybrać pewną próbę, np. tworząc wielowymiarową siatkę i jej węzły uznać za próbę (podejście deterministyczne), czy też wygenerować próbę losowo, bacząc aby była rozłożona równomiernie (podejście probabilistyczne).

---

Algorytm może być: ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) i przyjąć $x^{M(k)}$ za środek nowego otoczenia $x^{(k+1)}=x^{M(k)}=\alpha (x^{M(k)}-x^{(k)})+x^{(k)},\alpha =1$ a następnie przeszukiwać je tak jak poprzednio.

---

Algorytm może być też: odważny (wiem, że schody opadają w prawo, skaczę kilka stopni w prawo) i przesunąć środek kuli poszukiwań wzdłuż kierunku wyznaczonego przez różnicę wektorów $x^{M(k)}-x^k=d$ , tzn. ustalić środek nowej kuli w punkcie $x^{M(k)}=\alpha (x^{M(k)}-x^{(}k))+x^{(k)},\alpha >1$

---

---

Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez: J. A. Neldera i R. Meada i opublikowany w 1965 r.

---

Nie będziemy zagłębiali się w szczegóły algorytmu Neldera i Meada (jak ustalić próbę początkową, jak będąc odważnym zachować niezbędny stopień ostrożności itd.) odsyłając Czytelnika np. do monografii A. Stachurski, A. Wierzbicki: Podstawy optymalizacji, Oficyna Wydawnicza PW 1999, rozdział 3.10.

---

Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie.

---

Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się: Metodami obszaru zaufania (Trust region methods)

---

Przyjmujemy zatem, że dookoła punktu bieżącego $x^{(k)}$ została określona kula $\mathbb{𝕂}(x,r)$ i funkcja $x\mapsto f_M(x)$ będąca modelem zachowania się funkcji wyboru f w tej kuli, modelem dużo prostszym w analizie niż funkcja oryginalna. Do określenia modelu możemy posłużyć się intuicją opartą na rozważaniach punktu drugiego, co jak pamiętamy przekłada się na przeświadczenie, że funkcja celu dobrze daje się przybliżyć funkcją kwadratową $(APR)x\mapsto x^{T}Qx+c^{T}x+\sigma$

---

W takiej sytuacji przeszukanie otoczenia może oznaczać tylko jedno – szukanie punktu $x^{M(k)}$, minimalizującego funkcję modelującą na kuli. Punkt ten oczywiście będzie się różnił od rzeczywistego minimum funkcji celu f na kuli zaufania, ale mamy nadzieję, że niewiele, a co ważniejsze będzie spełniona nierówność $f(x^{M(k)}<f(x^{k-1})$ oznaczająca, że funkcja celu z kroku na krok maleje.

---

Ponieważ punkt$x^{M(k)}$ został wygenerowany w oparciu o model, to gdy kula jest za duża, może nie być właściwy – wartość funkcji celu może być w nim większa niż w punkcie centralnym kuli. Oznacza to, że w stosowny sposób trzeba dostosowywać promień kuli do zmienności funkcji celu. Zauważmy też, że przy takim podejściu, aby znaleźć rozwiązanie zadania optymalizacji bez ograniczeń trzeba rozwiązywać wielokrotnie zadanie z ograniczeniami ale z prostą funkcją wyboru – kwadratową funkcją aproksymującą.

---

W świetle ostatniej uwagi jest oczywiste, że algorytmy wykorzystujące omawiane podejście mogły liczyć na sukces dopiero w momencie, kiedy opracowano efektywne algorytmy rozwiązywania występujących w nich zadań $f_M(x)=x^{T}Qx+c^{T}x+\sigma \to min$ $p.o.(x-x^{(k)}{)}^T(x-x^{(}k))\le r^2$

---

Podstawowy algorytm obszaru zaufania Inicjalizacja Wybierz punkt początkowy $x^{(0)}$. Ustal początkowy obszar zaufania $T(x^{(0)}$). Podstaw k := 0. Kroki algorytmu Dla punktu $x^{(k)}$ wyznacz model $f_M(\cdot ;x^{(k)})$ funkcji celu w jego otoczeniu. Znajdź przybliżenie punktu ${\tilde{x}}^{(k)}$ Sprawdź czy wielkość obszaru zaufania została wybrana właściwie. Jeżeli tak, podstaw Parser nie mógł rozpoznać (nieznana funkcja „\tildex”): {\displaystyle \tildex^{(k)}:={x}^{(k)}} , idź do 5. W przeciwnym przypadku idź do 4. Zmniejsz obszar zaufania do TS, podstaw $T(x^{(k)}):=TS$, idź do 2. Jeżeli spełnione jest kryterium stopu, to $x^{(k)}$ przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 6. Sprawdź czy należy powiększyć obszar zaufania do TL. Jeżeli tak, podstaw $T(x^{(k)}):=TL$, idź do 7. W przeciwnym przypadku idź do 7. Podstaw k := k + 1, idź do 1. Wyjaśnień wymagają kroki 2, 3, 6 i oczywiście kryterium stopu.

---

---

---

Ciąg prostszych zadań daje ciąg rozwiązań $x_{k-0}^{(k)}{}^{\mathrm{\infty }}$ Naturalne pytanie które postawiliśmy, to kiedy go uciąć – które k uznać za ostatnie, dające rozwiązanie z dostateczną dokładnością. Był to zasygnalizowany problem testu stopu. Związane z tym problemem jest pytanie drugie – czy wygenerowany ciąg w ogóle jest zbieżny, a gdy jest, to czy jego granica jest rozwiązaniem zadania optymalizacji ? Jest to pytanie teoretyczne i odpowiemy na nie po konkretyzacji algorytmu w wykładzie siódmym.

---

Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3). Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy

---

Gdy znamy gradient, nierówność ta pozwala sprawdzić czy dany kierunek d jest kierunkiem poprawy. Mając ustalony kierunek poprawy powinniśmy poruszając się wzdłuż niego znaleźć punkt dający mniejszą niż w punkcie bieżącym wartość funkcji celu.

---

---

Zgodnie z określeniem poruszania się wzdłuż kierunku, znalezienie punktu $\overline{x}\in P(x^{(k)};d)\subset R^n$ jest równoważne ustaleniu pewnego $\overline{\alpha }\in R$ Zatem zmieniając $\alpha$ od zera do plus nieskończoności ruszamy się wzdłuż prostej $P(x^{(k)};d)$ w kierunku malenia funkcji celu. Konkretną wartość $\overline{\alpha }$ – długość kroku – możemy ustalić a priori. Intuicyjnie nie jest to najlepszy sposób, bo żeby zabezpieczyć się przed zbytnim przeskoczeniem minimum funkcji celu na zbiorze P(x(k);d) trzeba tą stałą długość kroku wybrać niewielką. Wobec tego można postępować tak: wybieramy duży krok początkowy ${\alpha }^{(0)}$, gdy $f(x^{(k)}+{\alpha }^{(0)}d)<f(x^{(k)})$ to ${\alpha }^{(0)}$ uznajemy za długość kroku, gdy przeciwnie – zmniejszamy ${\alpha }^{(0)}$ do ${\alpha }^{(1)}$), powtarzamy sprawdzenie czy wartość funkcji zmalała, itd. aż uzyskamy krok dający poprawę

---

Dokonujemy, jak mówimy minimalizacji w kierunku. Formułując to zadanie przybliżonej minimalizacji funkcji jednej zmiennej $\alpha (x^{(k)}$ i d są ustalone!) wykorzystaliśmy fakt, że zbiór dopuszczalny $P(x{(}^{k)};d)$ jest określony jednym ograniczeniem równościowym. Wprawdzie wiemy, że „ruszanie się” wzdłuż kierunku poprawy nie musi doprowadzić do minimum globalnego, ale na pewno poprawi wartość funkcji celu. O ile poprawi ? – Może poprawić bardzo niewiele, ale tak jak przy ustalaniu podstaw poprzednich metod, zgodnie z naszym podejściem optymistycznym, uważamy że ta poprawa będzie istotna. Jak pamiętamy przekonanie to ma podstawy formalne, ponieważ rozważania teoretyczne sugerują, że „porządne” funkcje są lokalnie wypukłe, a co za tym idzie nie powinno być kłopotów ze znalezieniem punktu lepszego niż bieżący. Przy wymyślaniu kryterium stopu pomocny może być warunek stacjonarności gradientu wskazujący na możliwość konstrukcji kryterium stopu w oparciu o jakąś miarę „małości” gradientu.

---

---

---

Bardziej formalnie przedstawioną procedurę minimalizacji opartą na generowaniu kierunków poprawy opisuje następujący podstawowy algorytm kierunków poprawy. Podstawowy algorytm kierunków poprawy Inicjalizacja Wybierz punkt początkowy $x^{(0)}$. Podstaw k := 0. Kroki algorytmu Dla punktu $x^{(k)}$ wyznacz kierunek poprawy $d^{(k)}$. Ustal długość kroku w kierunku poprawy ${\alpha }^{(k)}$.. Wylicz następny punkt podstawiając $x^{(k)}:=x^{(k)}+{\alpha }^{(k)}{d}^{(k)}$. Jeżeli spełnione jest kryterium (test) stopu, to $x^{(k)}$ przyjmij za rozwiązanie i stop. W przeciwnym przypadku idź do 5. Podstaw k := k + 1, idź do 1.

---

Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji.

---

---

Szukanie punktu dającego poprawę: w metodzie rozsiewania punktów próbnych jest to zadanie wyboru punktu najmniejszego ze skończonej ich liczby; w metodzie obszarów zaufania jest to zadanie wielo-wymiarowej minimalizacji przy ograniczeniach, najczęściej funkcji kwadratowej, zadanie ZKK; dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej, zadanie ZPK.

---

---

Zbieżność skończona, która ma miejsce wtedy gdy istnieje taka liczba K dla której $x{(}^{K)}=<math>x^o$</math>. Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm Simplex rozwiązywania zadań liniowych. Jednak jak pamiętamy, liczba iteracji może być bardzo duża, co oznacza, że na rozwiązanie zadania trzeba bardzo długo czekać. Metody punktu wewnętrznego nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod tego typu. A wniosek ogólny – z praktycznego punktu widzenia zbieżność skończona z bardzo dużym K może być gorsza niż zbieżność nieskończona, w sytuacji w której ciąg szybko zmierza do niewielkiego otoczenia rozwiązania. Znana Państwu z analizy matematycznej zbieżność wektorowego ciągu nieskończonego, zwana jest w teorii metod optymalizacji krótko zbieżnością (nieskończoną). Jest ona rozumiana dwojako: jako zbieżność do rozwiązania $x^o$, albo dla funkcji gładkich – zbieżność do punktu stacjonarnego gradientu, tzn. takiego wektora $\hat{x}$ , że $\mathrm{\nabla }f(\hat{x})=0$ Jak pamiętamy punkt może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie. Dlatego w niektórych wypadkach twórcom algorytmów udaje się udowodnić własność jeszcze słabszą: ciąg wektorów generowany przez algorytm zawiera podciąg zbieżny. Akceptacja zbieżności ostatniego rodzaju po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym “optymistycznym” podejściu do analizy sytuacji.

---

W tym przypadku rozwiązaniem równania $\mathrm{\nabla }f(\hat{x})=0$ jest $\hat{x}=(0,0)$ , a ten punkt ekstremum, nawet lokalnym, dla rozważanej funkcji nie jest. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony, są bardzo rzadkie.

---

---

Zbieżny ciąg $x^{(k)}{}^{\mathrm{\infty }}{}_{k=0}$ otrzymany w kolejnych krokach algorytmu, jest zbieżny a) liniowo, gdy dodatkowo Parser nie mógł rozpoznać (błąd składni): {\displaystyle \frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k \rightarrow\infty} \rho\>0} b) superliniowo, gdy dodatkowo $\frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k\to \mathrm{\infty }}0$ c) kwadratowo, gdy dodatkowo $\frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k\to \mathrm{\infty }}\rho \gg 0$ Definicje szybkości związane są z szybkością zbiegania do zera: postępu geometrycznego o dodatnim ilorazie mniejszym niż jeden, np. danego wzorem Parser nie mógł rozpoznać (błąd składni): {\displaystyle h^{(k)}=2^{-k} (\frac{2^{-(k+1)}}{2^{-k}}=\frac{1}{2}\ge 0) – zbieżność liniowa,} np. ciągu danego wzorem Parser nie mógł rozpoznać (błąd składni): {\displaystyle h^{(k)}=k^{-k},k\in 1 \infty (\frac{k^{-(k+1)}}{k^k}=\frac{1}{k}\rightarrow 0) – zbieżność superliniowa,} np. ciągu danego wzorem Parser nie mógł rozpoznać (błąd składni): {\displaystyle h^{(k)}=2^{-k},k\in 1 \infty (\frac{2^{-2^{k+1}}}{(2^{-2^k})^2}\rightarrow 0)– zbieżność kwadratowa.}

---

Na rysunku przedstawiono w skali logarytmicznej siedem pierwszych wyrazów wymienionych wyżej ciągów. Widać że zbieżność liniowa jest najwolniejsza, a kwadratowa najszybsza. Różne eksperymenty pokazały, że w zastosowaniach praktycznych szybkość liniowa jest do zaakceptowania gdy granica $\rho$ jest dostatecznie mała, nie większa niż $\frac{1}{4}$.

---

---

Pierwszy sposób został omówiony dokładnie w wykładzie poprzednim. Została pokazana ograniczoność możliwości jego stosowania. Ogólna zasada działania pozostałych trzech schematów jest taka sama i polega na naprzemiennym rozwiązywaniu dwu zadań: generacji zbioru podlegającego przeszukaniu i szukaniu w tym zbiorze punktu dającego poprawę (np. minimalizującego odpowiednio dobraną funkcję). W metodzie obszarów zaufania to zadanie poprawy jest wielowymiarową minimalizacją przy ograniczeniach, najczęściej funkcji kwadratowej. Dla metody kierunków poprawy jest to poszukiwanie punktu dającego akceptowalne zmalenie w stosunku do wartości w zerze (punkcie początkowym), odpowiednio określonej funkcji jednej zmiennej. Schematy te zostały przedstawione ogólnie i dla zastosowań praktycznych wymagają „doprecyzowania”. Zostanie to uczynione w następnych wykładach.

---

---

---