GKIW Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 15: | Linia 15: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_1.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_1.png|400px]] | ||
|valign="top"| | |valign="top"|'''Rzutowanie''' | ||
Rzutowanie jest przekształceniem przestrzeni trójwymiarowej na przestrzeń dwuwymiarową. Rzutowanie polega na poprowadzeniu prostej przez dany punkt obiektu i znalezieniu punktu wspólnego tej prostej z rzutnią. Wyznaczony punkt nazywany jest rzutem a prosta promieniem rzutującym. | |||
Powszechna definicja rzutu jako przekształcenia na płaszczyznę jest pewnym uproszczeniem gdyż rozpatruje się też np. rzuty na powierzchnię walca lub na wycinek sfery. Jednak rzeczywiście z rzutowaniem na płaszczyznę mamy najczęściej do czynienia (grafika komputerowa, fotografia). | |||
|} | |} | ||
| Linia 22: | Linia 26: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_2.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_2.png|400px]] | ||
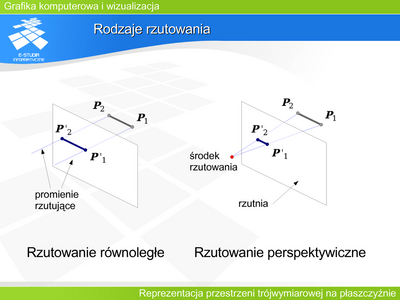
|valign="top"| | |valign="top"|'''Rodzaje rzutowania''' | ||
'''Rzutowanie równoległe''', gdy promienie rzutujące są prostymi równoległymi. Dodatkowo mówimy o '''rzutowaniu równoległym prostokątnym''', jeśli rzutnia jest prostopadła do kierunku rzutowania oraz o '''rzutowaniu równoległym ukośnym''' w każdym innym przypadku. | |||
'''Rzutowanie perspektywiczne''', gdy promienie rzutujące tworzą pęk prostych. Oczywiście, mówienie w tym przypadku o prostopadłości (lub nie) rzutni nie ma sensu, gdyż w rzutowaniu perspektywicznym dokładnie jeden promień może być prostopadły do płaszczyzny rzutni, a wszystkie pozostałe tworzą z nią kąty mniejsze od kąta prostego. | |||
'''Rzutowanie perspektywiczne''' jest często nazywane '''rzutowaniem środkowym lub centralnym'''. | |||
|} | |} | ||
| Linia 29: | Linia 39: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_3.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_3.png|400px]] | ||
|valign="top"| | |valign="top"|'''Właściwości rzutowania''' | ||
Z rzutowaniem równoległym mamy najczęściej do czynienia w różnego typu zastosowaniach technicznych np. rzuty prostokątne na 3 lub 6 płaszczyzn – tradycyjny rysunek techniczny. Rzutowanie równoległe nie pozwala przedstawić obiektu zgodnie z naszym wyobrażeniem – zgodnie z widzeniem człowieka. Pozwala natomiast zdefiniować wymiary przedmiotu i parametry technologiczne. | |||
Rzutowanie równoległe zachowuje równoległość prostych oraz proporcje długości odcinków równoległych | |||
Rzutowanie perspektywiczne pozwala uzyskać obraz zbliżony do postrzeganego przez człowieka. Trzeba jednak pamiętać o tym, że obraz na siatkówce oka powstaje w wyniku rzutu środkowego na wycinek sfery (w przybliżeniu). Zatem wszystkie promienie rzutujące będą w tym przypadku prostopadle padały na rzutnię. Oznacza to, że rzut na płaszczyznę będzie tylko przybliżeniem obrazu powstającego na siatkówce oka. | |||
Oczywiście dobór warunków rzutowania ma decydujący wpływ na późniejszy, mniej lub bardziej realistyczny odbiór obrazu. Jest to szczególnie istotne w przypadku zastosowania grafiki do generacji efektów specjalnych (lub całych ujęć) w kinematografii, a także w produkcji gier komputerowych, gdzie realistyczność odbieranego świata decyduje często o jakości gry. | |||
Naturalnym i najczęściej stosowanym układem współrzędnych związanym z rzutowaniem i obserwatorem jest lewoskrętny kartezjański układ współrzędnych. Kierunki osi 0X i 0Y są zgodne ze współrzędnymi definiującymi położenie na płaszczyźnie rzutni natomiast współrzędna Z określa odległość od obserwatora. | |||
Ponieważ położenie przedmiotów wyimaginowanego świata jest opisywane w układzie prawoskrętnym, to zachodzi konieczność nie tylko związania położenia obserwatora i kierunku rzutowania z układem świata, ale także zapewnienia zmiany skrętności układu. Trzeba o tym pamiętać definiując macierze opisujące odpowiednie operacje. Mówimy o układzie współrzędnych obiektu (sceny lub świata) i przestrzeni obiektu oraz układzie obserwatora (lub rzutu) i przestrzeni obserwatora. Takie rozdzielenie funkcjonalne znacznie ułatwia manipulację i definiowanie odpowiednich parametrów. Dodatkowo mówimy o układzie współrzędnych rzutni opisującym położenie elementów rzutu. | |||
|} | |} | ||
| Linia 36: | Linia 58: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_4.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_4.png|400px]] | ||
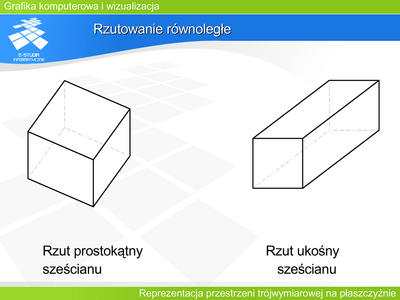
|valign="top"| | |valign="top"|'''Rzutowanie równoległe''' | ||
O '''rzutowaniu równoległym''' mówimy, że jest '''prostokątne''' wtedy, gdy promienie rzutujące są prostopadłe do płaszczyzny rzutni. W przeciwnym przypadku rzutowanie równoległe jest '''ukośne'''. | |||
Rzutowanie prostokątne jest powszechnie stosowane w mechanice. Podstawową zaletą takiego rozwiązania jest fakt, że wymiary rysunku odpowiadają wymiarom obiektu to znaczy długość odcinka równoległego do płaszczyzny rzutni jest równa długości rzutu tego odcinka. Aby na podstawie rzutu można było określić wymiary przedmiotu stosuje się zestaw trzech rzutów danego przedmiotu na rzutnie, które są wzajemnie prostopadłe. Ze względu na konieczność jednoznacznego przedstawienia widoków obiektu czasami (w przypadku bardzo złożonych elementów) stosuje się sześć rzutów. Tzn. są to rzuty na trzy płaszczyzny wzajemnie prostopadłe, ale dla każdej z nich wykonuje się po dwa rzuty dla wzajemnie przeciwnych kierunków. | |||
Można wykazać, że rzutowanie ukośne pozwala praktycznie dowolnie zmieniać proporcje wymiarów obiektu. To znaczy jeśli rozpatrzymy wzajemnie prostopadłe odcinki o takiej samej długości to można uzyskać dowolne proporcje ich rzutów dobierając odpowiednio kierunek rzutowania i położenie płaszczyzny rzutni. Z tego względu, w praktycznych zastosowaniach rzutowania równoległego ukośnego w mechanice najczęściej definiuje się rzut przez podanie zmian proporcji odległości wzdłuż każdej z osi układu współrzędnych, a nie przez podanie położenia rzutni i promieni rzutujących. Na przykład perspektywa kawalerska, perspektywa gabinetowa i perspektywa wojskowa są rodzajami rzutowania równoległego ukośnego zdefiniowanymi na tej zasadzie. | |||
Uzyskanie dowolnej zmiany proporcji wymiarów oznacza, że możliwe jest uzyskanie rzutu sześcianu jak na rysunku. '''Jest to całkowicie poprawny rzut równoległy ukośny sześcianu'''. Tylko że całkowicie niezgodny z naszym sposobem widzenia. | |||
|} | |} | ||
| Linia 43: | Linia 73: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_5.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_5.png|400px]] | ||
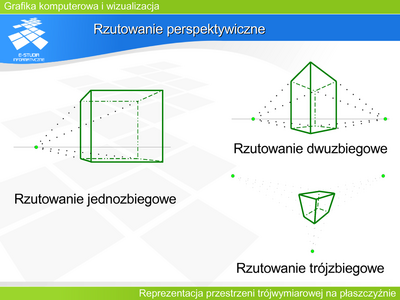
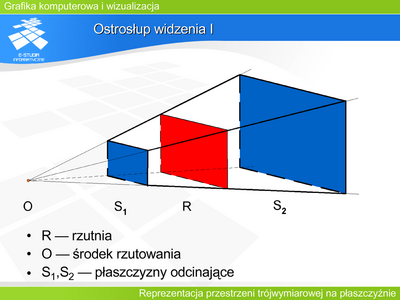
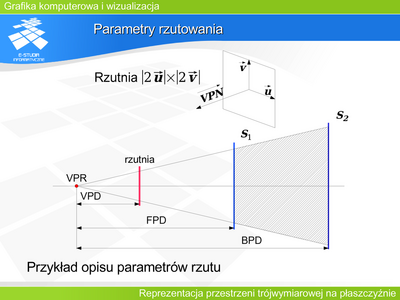
|valign="top"| | |valign="top"|'''Rzutowanie perspektywiczne''' | ||
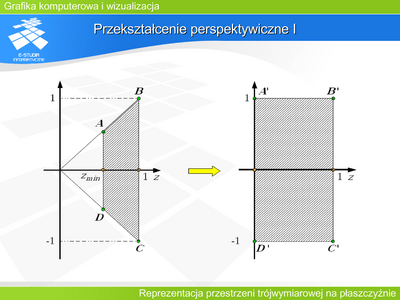
W każdym rzucie perspektywicznym istnieje przynajmniej jedna rodzina prostych równoległych i nie równoległych do rzutni, taka, że rzuty tych prostych przecinają się w jednym punkcie zwanym punktem zbiegu. W zależności od położenia rzutni względem obiektu mówimy o rzutowaniu perspektywicznym jednozbiegowym, dwuzbiegowym lub trójzbiegowym. | |||
Skrót perspektywiczny jest efektem wizualnym polegającym na tym, że wielkość rzutu perspektywicznego jest odwrotnie proporcjonalna do odległości obiektu od środka rzutowania. Z tego względu nie ma praktycznie możliwości uzyskania informacji o wymiarach obiektu na podstawie jego rzutu perspektywicznego. | |||
Z drugiej strony efekty wizualne uzyskane w rzutowaniu perspektywicznym są zbliżone do wrażeń wzrokowych oraz do efektów fotograficznych. | |||
|} | |} | ||
| Linia 50: | Linia 86: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_6.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_6.png|400px]] | ||
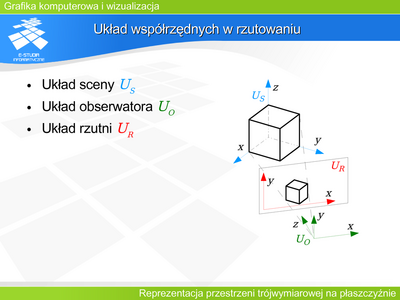
|valign="top"| | |valign="top"|'''Układ współrzędnych w rzutowaniu''' | ||
Rzutowanie jest realizowane w układzie obserwatora (lewoskrętnym). | |||
Przekształcenia i definiowanie obiektów w układzie sceny (prawoskrętnym). Jeśli przekształcenie punktu z jednego układu do drugiego opiszemy odpowiednią macierzą takiego przekształcenia, to funkcjonowanie obu układów współrzędnych ułatwi realizację tworzenie obrazu. | |||
Położenie punktów rzutu opisuje układ rzutni. Natomiast dodatkowo wyróżnia się układ urządzenia (fizyczny) związany bezpośrednio z urządzeniem wyświetlającym (drukującym) obraz | |||
|} | |} | ||
| Linia 57: | Linia 99: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_7.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_7.png|400px]] | ||
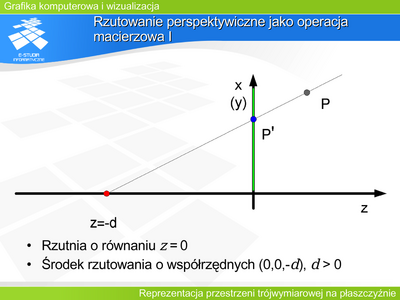
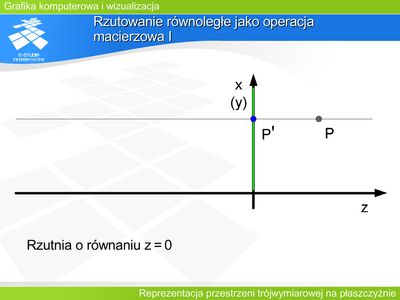
|valign="top"| | |valign="top"|'''Rzutowanie perspektywiczne jako operacja macierzowa I''' | ||
Rzutowanie może być opisane macierzowo, analogicznie do opisu operacji geometrycznych zaprezentowanych wcześniej. | |||
Rozpatrzmy rzutowanie perspektywiczne w przestrzeni obserwatora. Współrzędne opisują położenie w lewoskrętnym układzie współrzędnych obserwatora 0XYZ. | |||
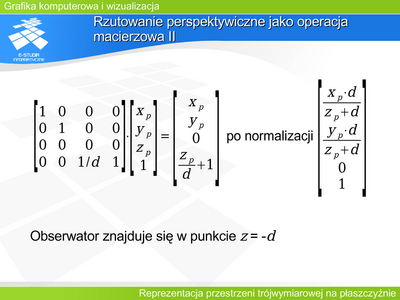
Niech obserwator (środek rzutowania) znajduje się w punkcie <math>(0,0,-d)</math> dla <math>d>0</math> a płaszczyzna rzutni ma równanie <math>z=0\,</math> - jak na rysunku. Macierz rzutowania będzie wtedy miała postać: | |||
:<math>\begin{bmatrix} | |||
1 & 0 & 0 & 0 \\ | |||
0 & 1 & 0 & 0 \\ | |||
0 & 0 & 0 & 0 | |||
0 & 0 & 1/d & 1 | |||
\end{bmatrix}</math> | |||
|} | |} | ||
| Linia 64: | Linia 121: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_8.png|400px]] | |valign="top" width="400px"|[[Grafika:GKIW_M5_Slajd_8.png|400px]] | ||
|valign="top"| | |valign="top"|''' | ||
|} | |} | ||
Wersja z 13:10, 12 gru 2006

|

|
|
|
|

|
|

|
|
|

|
|
|

|