TTS Moduł 2

Wykład

Fala elektromagnetyczna rozchodząca się w wolnej przestrzeni służy do transmisji sygnału w systemach radiokomunikacyjnych (radiofonia, telewizja naziemna i satelitarna, radiotelefonia). Fala wypromieniowana przez antenę nadawczą rozchodzi się we wszystkich kierunkach, choć oczywiście pewne kierunki są uprzywilejowane, o czym mówi charakterystyka anteny. Z punktu widzenia anteny odbiorczej oddalonej odpowiednio daleko, o wiele kilometrów, fala dochodząca do niej jest falą płaską. Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Fala płaska jest najprostszym typem fali elektromagnetycznej. Celem wykładu jest przedstawienie matematycznego opisu, własności i parametrów fali płaskiej rozchodzącej się w przestrzeni nieograniczonej wypełnionej stratnym dielektrykiem. Propagacja fali płaskiej w bezstratnej wolnej przestrzeni jest przypadkiem szczególnym, a jej własności wynikają z rozwiązania dla przypadku bardzej ogólnego, z uwzglenieniem strat ośrodka.

---

Na wstępie przypomnimy, znany z kursu fizyki, układ równań Maxwella w dziedzinie czasu. Równania te opisują tak pola statyczne (elektryczne albo magnetyczne) jak i zmienne w czasie pola elektromagnetyczne o dowolnej, ale zdeterminowanej zależności od czasu. Przedmiotem wykładu jest monochromatyczna fala elektromagnetyczna, czyli fala o ustalonej częstotliwości harmonicznych (cosinusoidalnych) zmian pól w czasie. W zagadnieniach dotyczących takich pól stosujemy rachunek symboliczny wykorzystujący operacje na funkcjach zespolonych w dziedzinie częstotliwości. Wprowadzimy wektory zespolone dla wielkości związanych z polem elektromagnetycznym, oraz sformułujemy równania Maxwella w postaci zespolonej. Przeprowadzimy uproszczoną klasyfikację ośrodków materialnych w oparciu o ich cechy elektryczne oraz poznamy zachowanie się dielektryków w obecności zewnętrznego pola elektrycznego cosinusoidalnie zmieniającego się w czasie. Z równań Maxwella w postaci zespolonej wyprowadzimy równania Helmholtza (odpowiednik równania falowego) dla pola elektrycznego i magnetycznego fali płaskiej rozchodzącej się w nieograniczonym ośrodku dielektrycznym. Na podstawie wyprowadzonych równań Helmholtza, wspomagając się równaniami Maxwella, znajdziemy matematyczny opis fali płaskiej rozchodzącej się w nieograniczonej przestrzeni, określimy jej własności i parametry. Omówimy również rodzaje polaryzacji płaskiej fali elektromagnetycznej.

---

Przypomnijmy podstawowe wielkości charakteryzujące pole elektromagnetyczne będące kompozycją pól elektrycznego i magnetycznego: Natężenie pola elektrycznego $\overrightarrow{E}$ jest wektorem (ma swoją wartość i kierunek), funkcją miejsca i czasu. Natężenie pola elektrycznego mierzymy w woltach na metr $[V/m]$. Natężenie pola magnetycznego $\overrightarrow{H}$ jest także wektorem, mierzymy jego wartość w amperach na metr $[A/m]$. Indukcja elektryczna $\overrightarrow{D}$ jest wektorem, mierzymy jej wartość w amperach razy sekunda na metr kwadratowy $[As/m^2]$, czyli kulombach na $m^2$ $[C/m^2]$. Indukcja magnetyczna $\overrightarrow{B}$ jest wektorem, mierzymy jej wartość w voltach razy sekunda na metr kwadratowy $[Vs/m^2]$. Ładunek elektryczny jest skalarnym źrodłem pola elektrycznego. W punkcie przestrzeni miarą ładunku jest jego gęstość objętościowa $\rho$, której jednostką jest kulomb na metr sześcienny $[C/m^3]$. Prądy elektryczne są wektorowymi źródłami pola magnetycznego. Wektor gęstości prądu $\overrightarrow{J}$ opisuje prąd w punkcie przestrzeni. Wartość $\overrightarrow{J}$ mierzymy w amperach na metr kwadratowy $[A/m^2]$. Wymienione powyżej pięć pól wektorowych i skalarne pole gęstości ładunku są funkcjami położenia (w prostokątnym układzie współrzędnych zależą od $(x,y,z)$ oraz czasu $t$. Wzajemne relacje między tymi polami określają równania Maxwella.

---

Pierwsze równanie Maxwella w postaci różniczkowej stwierdza, że rotacja wektora natężenia pola elektrycznego jest równa co do wartości szybkości zmian w czasie wektora indukcji magnetycznej. Zatem, zmiany indukcji magnetycznej powodują powstanie wirowego (niepotencjalnego) pola elektrycznego. Równanie to opisuje zjawisko indukcji elektromagnetycznej, której istotą jest indukowanie przez zmienne w czasie pole indukcji magnetycznej zmiennego pola elektrycznego, przy czym wektor natężenia pola elektrycznego jest w każdym punkcie przestrzeni prostopadły do wektora indukcji magnetycznej. Drugie równanie Maxwella stanowi, że rotacja wektora natężenia pola magnetycznego w punkcie przestrzeni jest równa wektorowi gęstości całkowitego prądu występującego w tym punkcie. Prawa strona równania zawiera dwa składniki: wektor gęstości prądu elektrycznego $\overrightarrow{J}$ , który jest sumą wektora gęstości prądu przewodzenia wynikającego z ruchu ładunków w materiale i wektora gęstości prądu unoszenia polegającego na ruchu naładowanych ciał; wprowadzony przez Maxwella prąd przesunięcia związany ze zmianami indukcji elektrycznej w czasie, którego wektor gęstości to $\partial \overrightarrow{D}/\partial t$ . Miarą gęstości prądu przesunięcia jest amper na metr kwadratowy $[A/m^2]$. Pomijając prąd przesunięcia stwierdzimy, że przepływ prądu elektrycznego powoduje powstanie wirowego pola magnetycznego o rotacji równej gęstości tego prądu. Prąd elektryczny jest więc źródłem wektorowym pola magnetycznego. Gdy występuje tylko prąd przesunięcia to drugie równanie Maxwella wyraża zjawisko indukcji magnetoelektrycznej polegające na indukowaniu przez zmienne pole indukcji elektrycznej zmiennego pola magnetycznego, przy czym wektor natężenia pola magnetycznego jest w każdym punkcie przestrzeni prostopadły do wektora indukcji elektrycznej. Z pierwszych dwóch równań Maxwella wynika, że zmiany w czasie indukcji magnetycznej powodują powstanie wirowego (niepotencjalnego) pola elektrycznego, a zmienna w czasie indukcja elektryczna wytwarza wirowe pole magnetyczne. Nie można odseparować od siebie pól elektrycznego i magnetycznego. Mówimy więc o polu elektromagnetycznym. Pola te mogą występować niezależnie tylko wtedy gdy nie zmieniają się w czasie. Dodatkowo, z omawianych równań wynika, że pola zmienne w czasie muszą być zmienne w przestrzeni (w przeciwnym razie rotacja jest równa zero). W trzech ostatnich równaniach Maxwella z lewej strony występuje dywergencja. Gdy dywergencja pola wektorowego nie jest równa zeru to pole nazywamy źródłowym, występują skalarne źródła tego pola. W przeciwnym przypadku pole jest bezźródłowe. Prawo Gaussa dla pola elektrycznego mówi, że dywergencja wektora indukcji elektrycznej równa jest objętościowej gęstość ładunku elektrycznego. Skalarnym źródłem pola indukcji elektrycznej są ładunki elektryczne. Prawo Gaussa dla indukcji magnetycznej informuje, że nie ma swobodnych ładunków magnetycznych. Pole indukcji magnetycznej jest bezźródłowe. Prawo zachowania ładunku mówi, że dywergencja gęstości prądu przewodzenia w określonym punkcie przestrzeni równa jest szybkości zmian w czasie gęstości objętościowej niezrównoważonego ładunku swobodnego. Skalarnym źródłem pola gęstości prądu przewodzenia jest zmiana ładunku w czasie.

---

Rozwiązanie szeregu zagadnień elektrodynamiki upraszcza się gdy zastosuje się rachunek symboliczny wykorzystujący operacje na funkcjach zespolonych. Wektorem zespolonym $\overrightarrow{E}$ nazywamy wektor, którego trzy składowe mogą być liczbami zespolonymi. Taki wektor jest jednoznacznie określony przez podanie sześciu uporządkowanych liczb lub dwóch wektorów rzeczywistych: $Re(\overrightarrow{E})$ oraz $Im(\overrightarrow{E})$ ; $\overrightarrow{E}=Re(\overrightarrow{E})+jIm(\overrightarrow{E})$ . Działania na wektorach zespolonych wykonujemy tak jak na wektorach rzeczywistych, przy czym należy pamiętać, że kwadrat jednostki urojonej należy zastąpić przez minus jeden. Przyjęto regułę, że wektory zespolone oznaczanę są kursywą, a wektory rzeczywiste literami prostymi.

---

Układ zespolonych równań Maxwella jest analogiczny do układu dla wektorów rzeczywistych, przy czym różniczkowanie po czasie $\partial /\partial t$ zastąpiono mnożeniem przez $j\omega$ . Rozwiązaniem układu równań są amplitudy zespolone zależne od zmiennych przestrzeni, na podstawie których wyznacza się pola rzeczywiste. Przykładowo, znamy amplitudę zespoloną $\overrightarrow{E}(x,y,z)={\overrightarrow{i}}_x|E_x(x,y,z)|exp(jArg{E}_x)$ Mnożymy ją przez $exp(j\omega t)$ i wyznaczamy część rzeczywistą, która jest poszukiwanym wektorem rzeczywistym, czyli $\overrightarrow{E}(x,y,z,t)=Re[\overrightarrow{E}(x,y,z)e^{j\omega t}={\overrightarrow{i}}_x|E_x(x,y,z)|cos(\omega t+Arg{E}_x)$

---

Dotychczas mówilismy o wektorach $\overrightarrow{E},\overrightarrow{D},\overrightarrow{H},\overrightarrow{B}$ określających pole elektromagnetyczne w taki sposób, jakby były one niezależne od siebie. Pierwsze dwa równania materiałowe wiążą ze sobą wymienione wektory w szekokiej klasie ośrodków (istnieją ośrodki, np. bianizotropowe, dla których związki między wektorami natężeń i indukcji pól są bardziej skomplikowane). Trzecie równanie materiałowe, nazywane wektorowym prawem Ohma, wiąże wektor gęstości prądu przewodzenia z wektorem natężeniam pola elektrycznego. Przenikalność elektryczna i konduktywność charakteryzują dielektryki, a przenikalność magnetyczna - magnetyki Przenikalność elektryczna $\epsilon$ to miara zdolności dielektryka do osłabiania zewnętrznego pola elektrycznego, ale również miara zdolności do koncentracji energii pola elektrycznego; Przenikalność elektryczną mierzymy w faradach na metr. Często posługujemy się bezwymiarowym pojęciem względnej przenikalności elektrycznej ${\epsilon }_w$, która jest $\epsilon$ unormowaną do przenikalności elektrycznej próżni ${\epsilon }_0$. Analogicznie można opisać przenikalność magnetyczną w stosunku do magnetyka, której miarą jest henr na metr. Normalizując $\mu$ do przenikalności magnetycznej próżni ${\mu }_0$ uzyskujemy względną przenikalność magnetyczną ${\mu }_w$ ośrodka. W niniejszym wykładzie będziemy zajmować się ośrodkami niemagnetycznymi, dla których ${\mu }_w=1$. Konduktywność $\sigma$ to miara zdolności środowiska do przepływu prądu przewodzenia, mierzona w siemensach na metr, a pośrednio miara liczby swobodnych nośników ładunku w jednostce objętości dielektryka. Gdy wektory występujące w równaniach materiałowych są rzeczywiste to parametry materiałowe są wielkościami rzeczywistymi. Dla pól cosinusoidalnie zmiennych w czasie parametry materiałowe w ogólności są wielkościami zespolonymi.

---

Ośrodki dzielimy na materialne i próżnię. Podano szereg przymiotników opisujących własności próżni, które należy zdefiniować. W tym celu dokonajmy pewnej uproszczonej klasyfikacji ośrodków materialnych ze względu na ich cechy elektryczne, a więc postać parametrów i równań materiałowych. Równania materiałowe wskazują na liniową zależność wektorów indukcji oraz gęstości prądu od natężeń pól. Oznacza to, że wielkości $\epsilon ,\mu ,\sigma$ nie zależą od natężeń pól i taki ośrodek nazywamy liniowym. Jeżeli przynajmniej jeden z parametrów ośrodka zależy od natężeń pól to ośrodek nazywa się nieliniowym. Ośrodek o zerowej konduktywności określmy, dla potrzeb czynionej klasyfikacji przyjmijmy, jako bezstratne. Takie materiały charakteryzują tylko dwa pozostałe parametry materiałowe. Materialny ośrodek jest jednorodny gdy jego parametry nie zależą od współrzędnych punktu. W przeciwnym przypadku mówimy o ośrodku niejednorodnym. Istnieją ośrodki, których parametry $\epsilon ,\mu ,\sigma$ zależą od częstotliwości. Ośrodki takie nazywamy dyspersyjnymi. Równania materiałowe w prezentowanej formie mają sens dla ośrodków dyspersyjnych tylko w przypadku sinusoidalnej zależności pól od czasu. Jeżeli wielkości $\epsilon ,\mu ,\sigma$ są niezależne od kierunku pól to ośrodek nazywamy izotropowym. Odpowiednie wektory występujące w poszczególnych równaniach materiałowych są do siebie równoległe. Gdy parametry ośrodka zależą od kierunku pól, to mówimy o ośrodku anizotropowym, którego własności nie mogą być opisane przez skalarne wielkości $\epsilon ,\mu ,\sigma$. Równania materiałowe mogą być prawdziwe dla ośrodka anizotropowego, ale wtedy parametry materiałowe są reprezentowane przez tensory. Zauważmy, że prędkość światła w próżni związana jest z jej parametrami materiałowymi. Pierwiastek ze stosunku przenikalności magnetycznej i elektrycznej ma wymiar ohm i wielkość tę nazywamy impedancją właściwą próżni.

---

Podział ośrodków na próżnię i ośrodki materialne nie jest przypadkowy. Jedynie próżnia jest ośrodkiem bezstratnym. Konduktywność ośrodków występujących w przyrodzie zawiera się w bardzo szerokich granicach od $\approx 10^{-17}S/m$ dla kwarcu do $6,1\cdot 10^{7}S/m$ dla srebra. Należy zadać pytanie, które ośrodki można uznać za bezstratne. Konduktywność ośrodka jest właściwym kryterium jego bezstratności tylko dla niskich częstotliwości. Dla wyższych częstotliwości poza stratami przewodzenia mamy do czynienia z tzw. stratami polaryzacji, które omówimy w dalszej części wykładu. Przyjmijmy arbitralnie, że ośrodek, w którym wartość prądu przesunięcia jest co najmniej trzy rzędy większy od prądu przewodzenia można uznać za bezstratny dielektryk. Przykładem takiego dielektryka jest suche czyste powietrze. 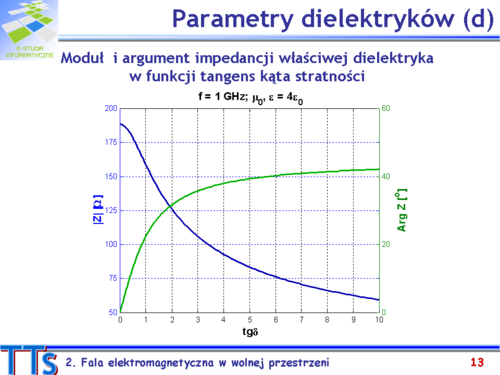Dla bezstratnych dielektryków, podobnie jak dla próżni, znając przenikalność elektryczną (przenikalność magnetyczna jest taka jak dla próżni) można obliczyć prędkość rozchodzenia się światła oraz impedancję właściwą. Obie wielkości maleją z pierwiastkiem przenikalności elektrycznej materiału.

---

Materiały dielektryczne powszechnie występują w technice mikrofalowej w konstrukcji tak linii transmisyjnych jak i elementów oraz podzespołów. Z tego względu ważne jest poznanie zachowania izotropowego dielektryka w zewnętrznym polu elektrycznym o sinusoidalnej zależności od czasu, stosując wektory zespolone. W przypadku braku zewnętrznego pola elektrycznego dielektryk można traktować jako elektrycznie obojętny. W momencie pojawienia się pola zewnętrznego dielektryk polaryzuje się, czyli następuje nieznaczne przemieszczenie się ładunków związanych z atomami i (lub) cząsteczkami. Wytwarzają one pole skierowane tak, aby przeciwdziałać polu zewnętrznemu i dlatego wypadkowe natężenie pola elektrycznego jest mniejsze niż natężenie pola zewnętrznego. Współczynnikiem proporcjonalności między zespolonymi wektorami indukcji i natężenia jest zespolona przenikalność elektryczna. W przypadku statycznym lub przy wolnych zmianach pola wektor indukcji elektrycznej jest w przybliżeniu w fazie z wektorem natężenia pola elektrycznego i część urojoną przenikalności elektrycznej można pominąć. Dla pól szybkozmiennych opóźnienie wektora indukcji względem wektora natężenia nie jest pomijalnie małe, wymienione wektory mają różne fazy. Część urojona przenikalności elektrycznej, która opisuje straty w ośrodku (grzanie) wywołane tłumieniem wibracji dipoli i tym samym opóźnienie wektora indukcji elektrycznej względem wektora pola elektrycznego, musi być ujemna (${\epsilon }^{″}$ jest dodatnie). Wprowadzenie zespolonej przenikalności elektrycznej pozwala w prosty sposób uwzględnić w opisie ośrodka skomplikowane procesy polaryzacji występujące w otaczających nas materiałach.

---

Źródłem strat przewodzenia w dielektryku jest prąd przewodzenia o gęstości określonej przez tzw. wektorowe prawo Ohma: .

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Słownik

• Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
• Mikrofale - zakres częstotliwości fal elektromagnetycznych od 300 MHz do 1000 GHz.
• Równania Maxwella - fundamentalne równania techniki mikrofalowej opisujące pole elektromagnetyczne w czasie i przestrzeni.
• Przenikalność dielektryczna $\epsilon$ i magnetyczna $\mu$ -Podstawowe parametry opisujące właściwości przestrzeni odpowiednio dla pola elektrycznego i magnetycznego.
• Podstawowe parametry pola elektromagnetycznego:
  • Natężenie pola elektrycznego $[V/m]$ .
  • Natężenie pola magnetycznego $[A/m]$ .
• Indukcja pola elektrycznego $D$ - wielkość wektorowa proporcjonalna do natężenia pola elektrycznego i przenikalności dielektrycznej.
• Indukcja pola magnetycznego $B$ - wielkość wektorowa proporcjonalna do natężenia pola magnetycznego i przenikalności magnetycznej.
• I prawo Maxwella - z pierwszego równania Maxwella widać że zmienne pole magnetyczne jest źródłem zmiennego pola elektrycznego
  • W postaci całkowej jest zapisem prawa Faradaya i wiąże ze sobą zmianę strumienia indukcji magnetycznej przenikającego powierzchnię $S$ z polem elektrycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię (zal. 2-1).
  • W postaci różniczkowej I prawo Maxwella mówi, że rotacja pola elektrycznego jest równa pochodnej indukcji magnetycznej po czasie (zal.2-6).
• II prawo Maxwella - z drugiego równania Maxwella widać że źródłem zmiennego pola magnetycznego jest zmienny w czasie prąd lub zmienne pole elektryczne.
  • W postaci całkowej jest zapisem prawa Ampera i wiąże ze sobą zmianę strumienia indukcji elektrycznej i prąd przenikający powierzchnię $S$ z polem magnetycznym $E$ całkowanym wzdłuż zamkniętego konturu $C$ otaczającego tą powierzchnię (zal. 2-2).
  • W postaci różniczkowej II prawo Maxwella mówi nam że rotacja pola magnetycznego jest równa pochodnej indukcji elektrycznej i prądu po czasie (zal.2-6).
• III prawo Maxwella - jest zapisem prawa Gaussa dla pola elektrycznego i mówi, że źródłem pola indukcji elektrycznej są ładunki elektryczne.
  • W postaci całkowej prawo to mówi że strumień wektora indukcji pola elektrycznego $D$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ równy jest zgromadzonemu w tej objętości ładunkowi (zal 2-3).
  • W postaci różniczkowej prawo to mówi że divergencja (rozbieżność) wektora indukcji elektrycznej jest równa gęstości ładunku elektrycznego (zal.2-6).
• IV prawo Maxwella - jest zapisem prawa Gaussa dla pola magnetycznego i mówi, że pole magnetyczne jest bezźródłowe.
  • W postaci całkowej prawo to mówi że strumień wektora indukcji pola magnetycznego $B$ wypływający z objętości $V$ przez zamkniętą powierzchnię $S$ jest równy 0 co znaczy że pole magnetyczne jest bezźródłowe (zal. 2-4).
  • W postaci różniczkowej prawo to mówi, że divergencja (rozbieżność) wektora indukcji magnetycznej jest równa 0, co również znaczy że pola magnetyczne jest bezźródłowe (zal1-6).
• Równanie ciągłości prądu - opisuje relacje między prądem i ładunkiem elektrycznym.
  • W postaci całkowej prawo to mówi nam, że prąd przewodzenia wypływający przez powierzchnię $S$ zamkniętej objętości V równy jest szybkości zmian ładunku w tej objętości (zal.2-5).
  • W postaci różniczkowej prawo to mówi nam, że źródłem pola gęstości prądów jest zmiana gęstości ładunku w czasie (zal 2-6).
• Parametry materiałowe ośrodka dla pola elektromagnetycznego:
  • Przenikalność dielektryczna $\epsilon$ - określa relację między natężeniem pola elektrycznego a jego indukcją (zal. 2-11)
  • Przenikalność magnetyczna $\mu$ - określa relację między natężeniem pola magnetycznego a jego indukcją (zal. 2-11)
  • Konduktywność $\sigma$ - określa relację między natężeniem pola elektrycznego a gęstością prądu przewodzenia ( zal 2-11).
• Rodzaje ośrodków pod katem właściwości dla pola elektromagnetycznego:
  • Ośrodki liniowe i nieliniowe.
  • Ośrodki jednorodne i niejednorodne.
  • Ośrodki dyspersyjne i niedyspersyjne. Parametry materiałowe ośrodka dyspersyjnego zależą a ośrodka niedyspersyjnego nie zależą od częstotliwości.
  • Ośrodki izotropowe i anizotropowe. Parametry materiałowe ośrodka izotropowego nie zależą zaś ośrodka anizotropowego zależą od kierunku pola
• Warunki brzegowe na granicy dwóch dielektryków:
  • Nie ma prądów i ładunków powierzchniowych.
  • Składowe normalne wektorów indukcji $D$ i $B$ oraz składowe styczne wektorów natężenia pól $E$ i $H$ są ciągłe.
• Warunki brzegowe na granicy dielektryk idealny przewodnik: W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości:
  • Pole elektryczne musi być prostopadłe do przewodnika.
  • Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości Parser nie mógł rozpoznać (błąd składni): {\displaystyle \rho\,\} równej indukcji elektrycznej $D$.
  • Pole magnetyczne musi być styczne do przewodnika.
  • Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej $j$ równej $H$.
• Równania Helmholtza - równania falowe dla pól harmonicznych w zapisie zespolonym.
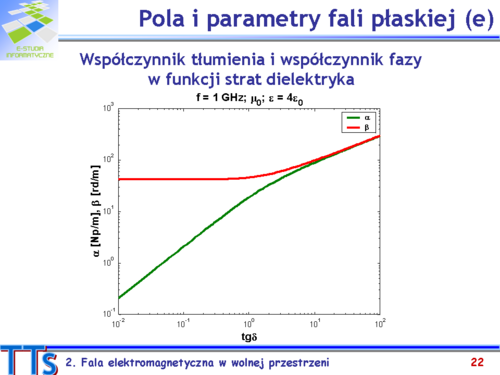
• Stała propagacji – funkcja parametrów materiałowych ośrodka (zal 2-38). Wartość decyduje o szybkości zmian parametrów fali wzdłuż kierunku propagacji.
• Stała tłumienia część rzeczywista stałej propagacji, decyduje o szybkości strat mocy fali wzdłuż kierunku jej propagacji (zal. 2-51a)
• Stała fazowa część urojona stałej propagacji, decyduje o szybkości zmian fazy fali ( zal. 2-51b, 2-52b).
• Prędkość fazowa fali - prędkość z jaką przesuwa się płaszczyzna stałej fazy fali.
• Prędkość grupowa fali - jest prędkością przepływu energii.
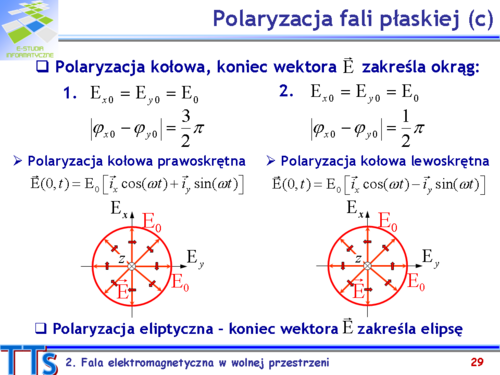
• Fala płaska - Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Powierzchnia ekwifazowa fali płaskiej jest płaszczyzna prostopadłą do kierunku propagacji.
• Właściwości fali płaskiej - fala płaska jest falą typu TEM (Transverse Electro-Magnetic)
  • Wektory $E$ i $H$ fali TEM leżą w płaszczyźnie prostopadłej do kierunku propagacji i są prostopadłe względem siebie.
  • Zwrot iloczynu wektorowego pola $E$ razy pole $H$ wyznacza kierunek propagacji a jego moduł gęstość mocy fali.
  • Impedancja falowa (stosunek wartości wzajemnie prostopadłych składowych pola $E$ i $H$) fali płaskiej jest równy impedancji właściwej ośrodka.

---

Bibliografia

1. Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
2. Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
3. Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
4. Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.

---