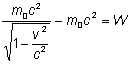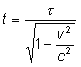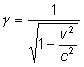PF Moduł 6

Wykład

---

Wstęp Mechanika oparta na równaniach dynamiki Newtona i transformacji Galileusza uznawana była przez ponad dwa wieki za teorię rządzącą ruchem wszelkich ciał materialnych. Jednak okazuje się, że prawa te mają charakter przybliżony. Doskonale zgadzają się z doświadczeniem, ale tylko dla prędkości znacznie mniejszych od prędkości światła. Poprawna teoria nazywa się mechaniką relatywistyczną. Mechanika newtonowska jest przybliżeniem mechaniki relatywistycznej dla $v<<c$ . Wiele wniosków mechaniki relatywistycznej kłóci się z tak zwanym „zdrowym rozsądkiem” i doświadczeniem naszego życia codziennego. Przyczyna tego jest prosta – w życiu codziennym nie spotykamy się z prędkościami relatywistycznymi, czyli porównywalnymi z prędkością światła. Intuicja człowieka ukształtowana jest przez nasze postrzeganie świata, a ono zdeterminowane jest przez możliwości ludzkich zmysłów. Poznanie fizyki relatywistycznej jest próbą przekroczenia ograniczeń, jakie nakłada na nas postrzeganie świata naszymi niedoskonałymi zmysłami i zobaczenia, jakim jest świat naprawdę

---

Prędkość światła Zgodnie z mechaniką Newtona prędkość kamienia wyrzuconego z poruszającego się pojazdu równa jest sumie prędkości pojazdu i prędkości, z jaką wyrzucony został kamień. Spodziewalibyśmy się, że tak samo będzie z prędkością impulsu świetlnego wysłanego z tego pojazdu. Jednak doświadczenie jest sprzeczne z tym intuicyjnym rozumowaniem! W 1889 roku Michelson i Morley stwierdzili, że prędkość ruchu Ziemi na orbicie okołosłonecznej nie dodaje się do prędkości światła, ani od niej nie odejmuje. Pomiar prędkości światła został wykonany za pomocą interferometru Michelsona. Światło ze źródła zostaje rozszczepione na dwie prostopadłe wzajemnie wiązki przez półprzezroczyste zwierciadło. Oba promienie po odbiciu od zwierciadeł spotykają się na ekranie, gdzie powstaje obraz interferencyjny. Jeśli ustawimy zwierciadła tak, aby nastąpiło wzmocnienie, a następnie obrócimy aparaturę o 900, to powstały nowy obraz interferencyjny powinien wyglądać inaczej, jeśli prędkość światła w kierunku ruchu Ziemi i w kierunku prostopadłym różnią się. Po wielokrotnych próbach Michelson i Morley nie zaobserwowali żadnego efektu.

---

Wniosek: prędkość światła jest stała dla każdego obserwatora!

---

Niezależność prędkości światła od ruchu układu odniesienia ma poważne konsekwencje dla naszego pojmowania czasu. W fizyce klasycznej czas płynie jednakowo w każdym układzie odniesienia i zdarzenia jednoczesne w jednym układzie są też jednoczesne w każdym innym. Wyobraźmy sobie wagon jadący z prędkością v. Pośrodku wagonu stoi podróżny. Załóżmy, że w chwili $t=t_0$ podróżny mija obserwatora stojącego obok torów. W tej samej chwili obserwator widzi dwa pioruny uderzające w końce wagonu. Uderzenia piorunów to dla niego zdarzenia jednoczesne. A co widzi pasażer? Zobaczy on najpierw błysk z prawej strony a później z lewej, bo zanim światło do niego dotrze, pociąg przebędzie pewną drogę w prawo. Pasażer wie, że uderzenia piorunów były równoodległe (stoi pośrodku wagonu), więc skoro najpierw ujrzał błysk z prawej a potem z lewej, wywnioskował, że pioruny uderzyły niejednocześnie. Widzimy, że równoczesność zdarzeń jest pojęciem względnym i wyciągamy wniosek, że czas biegnie różnie w różnych układach odniesienia. Zauważmy, że przyczyną względności równoczesności zdarzeń jest skończona prędkość rozchodzenia się światła. Gdyby błysk świetlny biegł nieskończenie szybko, pasażer oba pioruny zaobserwowałby jednocześnie tak, jak obserwator przy torach.

---

Równoważność układów inercjalnych dotyczy nie tylko praw mechaniki, jak w fizyce klasycznej, ale również elektromagnetyzmu. Nie można doświadczalnie stwierdzić, czy układ inercjalny porusza się, czy jest w spoczynku.

---

Transformacja Lorentza Transformacja to przepis, jak od współrzędnych w jednym układzie odniesienia przejść do współrzędnych w innym układzie. Klasyczna transformacja Galileusza zakłada istnienie absolutnego czasu jednakowego we wszystkich układach inercjalnych Parser nie mógł rozpoznać (błąd składni): {\displaystyle (t = t’)} . Jeśli ciało porusza się w układzie $O^{\prime }$ z prędkością $\overrightarrow{u^{\prime }}$ , to zgodnie z tą transformacją jego prędkość w układzie O jest równa $\overrightarrow{u}=\overrightarrow{u^{\prime }}+\overrightarrow{v}$ Jeśli w układzie $O^{\prime }$ będzie wysłany impuls światła z prędkością c, to jego prędkość w układzie $O^{\prime }$ byłaby większa od c, a to jest sprzeczne z doświadczeniem. Stałość prędkości światła w każdym układzie wymaga zmiany transformacji. Nowa transformacja musi zapewnić stałość prędkości światła niezależnie od tego, w którym układzie odniesienia prędkość ta jest rozpatrywana. Powinna też przechodzić w transformację Galileusza dla małych prędkości.

---

Transformacja Galileusza została zastąpiona przez transformację Lorentza. Zauważmy, że współrzędne przestrzenne i czasowe nie są rozdzielone, jak w transformacji Galileusza. Czas jest zależny od współrzędnej przestrzennej. Oznacza to, że nie ma czasu absolutnego jednakowego dla wszystkich układów.

---

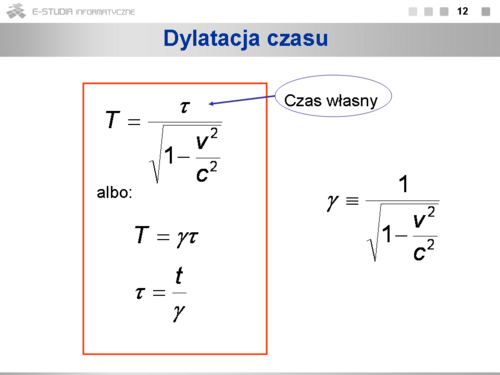
Zdefiniujmy wielkość $\gamma$ zwaną czynnikiem Lorentza. Czynnik ten jest zawsze większy od jedności, bo jak niebawem się przekonamy $v<c$. Wzory transformacji Lorentza mają prostszą postać.

---

Odwrotną transformację otrzymamy, jeśli zauważymy, że układ O porusza się względem układu $O^{\prime }$ z prędkością $-\overrightarrow{v^{\prime }}$ . Nietrudno zauważyć, że transformacja Lorentza przechodzi w transformację Galileusza, kiedy v dąży do 0, czyli dla prędkości małych w porównaniu z c.

---

Zasada względności i zasada stałości prędkości światła rewolucjonizuje nasze pojmowanie czasu. Zastosujmy te zasady do prostego „zegara świetlnego”. Jest to rurka z dwoma doskonale odbijającymi zwierciadłami na obu końcach. Wewnątrz porusza się impuls świetlny, który odbija się od zwierciadeł i biegnie tam i z powrotem. Tyknięciem zegara, czyli zmierzonym odstępem czasu, będzie czas, w jakim impuls przejdzie od zwierciadła dolnego do górnego. Początkowo (t = 0) dwa takie zegary tykają synchronicznie. Czas między kolejnymi odbiciami wynosi $\tau$, a więc długość zegara równa jest $c\tau$. Zegar B porusza się w prawo z prędkością v. Czy obserwatorowi A będzie wydawało się, że poruszający względem niego zegar B będzie krótszy lub dłuższy? Wyobraźmy sobie, że na końcu zegara B przymocowaliśmy pędzelek, który przy mijaniu zegara A namaluje na nim kreskę. Jeśli by ta kreska wypadła poniżej krawędzi, to obserwator A będzie widział poruszający względem niego zegar B jako skrócony, natomiast obserwator B zobaczy poruszający się zegar A wydłużony. Taka obserwacja jest sprzeczna z zasadą względności – efekty obserwowane w obu układach powinny być takie same. Wnioskujemy stąd, że długości zegarów ( i wszystkich odcinków prostopadłych do prędkości) powinny być równe. Po upływie czasu $\tau$ obserwator A (spoczywający) stwierdzi, że impuls świetlny w zegarze B przebył dłuższą drogę niż $c\tau$, bo musi biec po przekątnej. Ponieważ jednak prędkość światła jest stała, zajęło mu to więcej czasu. Czas między tyknięciami zegara B wynosi $T>\tau$. Stosując twierdzenie Pitagorasa do trójkąta widocznego na rysunku dostaniemy: $(cT{)}^2=(vT{)}^2+(c\tau {)}^2$ , stąd

---

Według spoczywającego obserwatora czas między dwoma tyknięciami zegara jest dłuższy, gdy zegar się porusza. Każdy obserwator widzi, że poruszający się względem niego zegar tyka $\gamma$ razy wolniej. Odstęp czasu między dwoma zdarzeniami, które obserwator widzi w tym samym punkcie przestrzeni, nazywamy czasem własnym. To najkrótszy czas jaki można zaobserwować między danymi zdarzeniami. Opisane zjawisko to dylatacja czasu wynikająca z równań transformacji Lorentza. Efekt ten możemy opisać następująco: w określonym miejscu (ustalone współrzędne przestrzenne) jednego układu, na przykład B, zachodzi pewne zjawisko, którego czas trwania wynosi $\tau$. W układzie A, względem którego układ B porusza się z prędkością v, zjawisko to zachodzi w różnych miejscach (różne współrzędne przestrzenne początku i końca zjawiska) i stąd wynika inny czas trwania tego zjawiska. Należy podkreślić, że spowolnienie upływu czasu w układzie poruszającym się względem obserwatora jest jak najbardziej realne. Zjawisko to jest obserwowane przez fizyków, którzy mierzą czas życia rozpadających się cząstek, na przykład mezonów $\pi$. Kiedy cząstka porusza się w układzie laboratoryjnym z prędkością bliską prędkości światła, jej czas życia ulega wydłużeniu, co bez trudu można sprawdzić doświadczalnie.

---

Wyobraźmy sobie hipotetyczny pojazd, poruszający się z prędkością relatywistyczną. Kiedy mijał stację A, zegar na stacji i zegar pokładowy wskazywały godzinę dwunastą. Na stacji B jest zegar zsynchronizowany z zegarem na stacji A. Gdy pojazd dojechał do stacji B, dróżnik zanotował godzinę 12.12, ale stwierdził, że zegar pokładowy wskazywał dopiero 12.05. Jeśli by rakietą podróżował jeden z braci bliźniaków, a drugi został na Ziemi, to obserwatorzy na Ziemi widzieliby, że podróżujący brat starzeje się wolniej. Ale przecież to samo widziałby bliźniak podróżnik – jego brat oddala się od niego wraz z Ziemią, a więc też starzeje się wolniej. Efekt dylatacji czasu jest zupełnie symetryczny w układach inercjalnych. Co więc będzie, gdy podróżnik wróci i spotka się ze swym bratem? Odpowiedź jest zaskakująca – podróżnik będzie młodszy! Jego rakieta nie mogła być układem inercjalnym, skoro wróciła na Ziemię. Musiała hamować, zmienić kierunek ruchu, a potem przyspieszyć. Te dwa układy rakieta i Ziemia nie są symetryczne, jeden z nich (nieinercjalny) jest wyróżniony. Opisany tu przykład to tak zwany „paradoks bliźniaków”, często dyskutowany, gdy rozważamy efekty relatywistyczne.

---

Pręt o długości l spoczywa w układzie O. Jaka jest długość $l^{\prime }$ tego pręta zmierzona w układzie $O^{\prime }$, który porusza się z prędkością $\overrightarrow{v}$ ? Aby dowiedzieć się, jaka jest długość poruszającego się pręta, obserwator z układu $O^{\prime }$ powinien zmierzyć odległość między jego końcami w tym samym momencie. Wyrażamy $l^{\prime }$ jako różnicę współrzędnych $z_2\text{'}$ i $z_1\text{'}$ zmierzonych w tej samej chwili czasu $t^{\prime }$ i korzystamy z transformacji Lorentza, podstawiając tę samą wartość $t^{\prime }$ dla obu końców pręta. Otrzymany wynik oznacza, że pręt poruszający się względem obserwatora ma mniejszą długość niż w układzie, w którym ten pręt spoczywa. Kontrakcja (skrócenie) długości zachodzi tylko w kierunku ruchu. Kontrakcja długości jest w pewnym sensie skutkiem istnienia „nierównoczesności czasowej” zdarzeń. Jeśli pomiary położenia końców pręta w jednym układzie są równoczesne, to w drugim układzie są nierównoczesne i odwrotnie. Dylatacja czasu jest w pewnym sensie skutkiem istnienia „nierównoczesności przestrzennej” zdarzeń. Jeśli pomiary czasu trwania zjawiska w jednym układzie zachodzą w określonym miejscu (przestrzennie), to w drugim układzie zachodzą w różnych miejscach i odwrotnie. A przyczyną obu efektów jest wymieszanie współrzędnych przestrzennych i czasowych w równaniach transformacji Lorentza.

---

Wykres pokazuje, jaką długość dla nieruchomego obserwatora będzie miał poruszający się pręt o długości 1 m. Na osi odciętych odłożony jest stosunek prędkości pręta do prędkości światła. Widać, że zauważalne skrócenie lorentzowskie występuje dopiero przy prędkości około 0,2•c. Kiedy prędkość zbliża się do prędkości światła, długość pręta dąży do zera!. Jednak nie dojdzie do zniknięcia pręta, ponieważ pręt nigdy nie osiągnie prędkości światła, jak zobaczymy później.

---

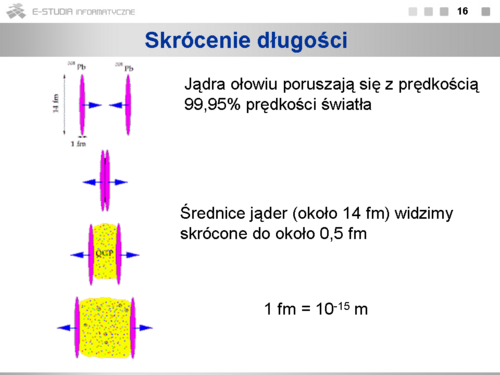
Poglądowa ilustracja zderzenia jąder ołowiu przyspieszonych do energii rzędu kilkudziesięciu tysięcy megaelektronowoltów. W wyniku skrócenia Lorentza kształt ich ze zbliżonego do kuli przekształcił się w formę dysków. Zauważmy bowiem, ze wymiary ciał skracają się tylko w kierunku ruchu. Środkowy obszar pokazany kolorem żółtym, to poszukiwany obecnie nowy stan materii zwany plazmą kwarkowo-gluonową. Zainteresowanych tymi zagadnieniami odsyłamy do strony internetowej Europejskiego Laboratorium Fizyki Cząstek CERN (http://www.cern.ch).

---

Czasoprzestrzeń W zakresie prędkości nierelatywistycznych (transformacja Galileusza) długość odcinka i przedział czasowy są jednakowe w każdym układzie odniesienia. Mówimy, że te wielkości są niezmiennikami transformacji Galileusza. Jednak dla prędkości porównywalnych z prędkością światła ani długość, ani przedział czasu nie są jednakowe w różnych układach odniesienia. Współrzędne przestrzenne i czasowe są od siebie zależne – tworzą czterowymiarową czasoprzestrzeń (trzy wymiary przestrzenne, czwartym wymiarem jest czas pomnożony przez c). Każdemu punktowi w czasoprzestrzeni odpowiada określone zdarzenie. Odpowiednikiem odległości między dwoma punktami w trójwymiarowej przestrzeni $\mathrm{\Delta }l$ jest interwał czasoprzestrzenny $\mathrm{\Delta }s$ - odległość między dwoma punktami w czasoprzestrzeni. Zauważmy, że odległość ta jest niezerowa nawet wtedy, gdy zdarzenia zachodzą w tym samym punkcie przestrzeni trójwymiarowej. Interwał czasoprzestrzenny jest niezmiennikiem transformacji Lorentza.

---

Punkt w czasoprzestrzeni nosi nazwę punktu świata, a zbiór punktów opisujących przemieszczenia danego ciała w czasie i przestrzeni tworzy linię świata. Linie te mieszczą się wewnątrz stożka zwanego stożkiem świetlnym lub stożkiem Minkowskiego. Stożek ten opisany jest równaniem $c^2\cdot \mathrm{\Delta }{t}^2=x^2+y^2+z^2=l^2$ . Trajektorie wszystkich sygnałów, które rozchodzą się z danego punktu O z prędkością światła znajdują się na powierzchni tego stożka. Wszystkie trajektorie ruchów o prędkościach mniejszych mieszczą się wewnątrz stożka. Stożek ten określa przeszłość i przyszłość zdarzenia O. Wszystko co w przeszłości mogło mieć wpływ na zdarzenie O mieści się w dolnej części stożka. Wszystko co może stanowić przyszłość tego zdarzenia mieści się w części górnej. Wszystkie zdarzenia z obszaru "gdzie indziej" ani nie mogły mieć wpływu na zdarzenie O w przeszłości, ani nie mogą mieć w przyszłości; nie pozostają z tym zdarzeniem w żadnym stosunku przyczynowym. Linia zielona, to linia świata relatywistycznej cząstki (poruszającej się z prędkością v), czyli zbiór zdarzeń, polegających na znalezieniu się tej cząstki w określonym miejscu w określonym czasie. Dla każdego takiego zdarzenia można wyznaczyć stożek przyszłości i przeszłości.

---

Wiemy, że światło biegnie od Słońca do Ziemi około 8 min. Obserwator znajduje się na Ziemi w wierzchołku stożka świata. W chwili t = 0 Słońce jest w punkcie na osi l (czerwone koło) . Aktualny stan Słońca jest niedostępny obserwacjom. Nawet jeśliby Słońce znikło, to dowiemy się o tym dopiero po 8 minutach od tego zdarzenia. Obraz Słońca widoczny na niebie to Słońce sprzed 8 minut (pomarańczowe koło na wykresie)

---

Transformacja prędkości Zapiszmy współrzędne wektora prędkości w spoczywającym układzie odniesienia O i zadanej w tym układzie chwili czasu t. Podobnie czynimy dla drugiego układu, poruszającego się względem pierwszego z prędkością $v_0$. Wszystkie wielkości odnoszące się do drugiego układu będziemy oznaczać symbolem (‘),"prim",

---

Korzystając z transformacji Lorentza obliczamy różniczki dx, dy, dz i dt oraz dx’, dy’, dz’, i dt’.

---

Możemy teraz wyznaczyć składowe prędkości dzieląc pierwsze trzy równania określające transformacje przyrostów współrzędnych przez czwarte, określające przyrost czasu. Gdy prędkość $v_0$ będzie mała w stosunku do prędkości światła, to wzory przechodzą we wzory otrzymane za pomocą transformacji Galileusza.

---

Podobnie możemy wyrazić składowe prędkości w układzie O’ przez składowe prędkości w układzie O.

---

Sprawdźmy jaka będzie prędkość światła zmierzona przez obserwatora w układzie O, jeśli źródło światła porusza się względem obserwatora z prędkością $v_0$. Oczywiście prędkość światła w obu układach jest taka sama i wynosi c. Nie jest to niespodzianką, ponieważ wzory na transformację prędkości wyprowadziliśmy z transformacji Lorentza, a te zostały tak sformułowane, aby zapewnić stałość prędkości światła w każdym układzie odniesienia.

---

Dynamika relatywistyczna II zasada dynamiki Ważną wielkością w fizyce jest pęd zdefiniowany: $\overrightarrow{p}=m\cdot \overrightarrow{v}$ . Szczególną rolę odgrywa zasada zachowania pędu, przy czym zasada ta jest spełniona niezależnie od tego w jakim układzie odniesienia znajduje się obserwator. Aby zapewnić niezależność zasady zachowania pędu od układu odniesienia, należy zmodyfikować definicję pędu. Masa nie może być stała – powinna rosnąć wraz z prędkością. Wielkość $m_0$ nazywamy masą spoczynkową. Pęd relatywistyczny nie jest wprost proporcjonalny do prędkości – rośnie szybciej z prędkością.

---

Gdy prędkość ciała dąży do prędkości światła, jego masa dąży do nieskończoności. Oznacza to, że w miarę wzrostu prędkości potrzeba coraz większej energii, aby dalej zwiększać prędkość. Osiągnięcie prędkości światła wymagałoby nieskończonej energii. Dlatego żadne ciało o niezerowej masie spoczynkowej nie może poruszać się z prędkością światła.

---

Najbardziej ogólną postać II zasady dynamiki wyraża równanie przyrównujące szybkość zmiany wektora pędu do działającej siły. Jednak obliczenie pochodnej $\frac{d\overrightarrow{p}}{dt}$ w przypadku relatywistycznym wymaga uwzględnienia tego, że masa jest funkcją prędkości. Widzimy, że przyspieszenie nie jest już wprost proporcjonalne do siły. Co więcej, jeśli kierunek prędkości nie będzie taki sam jak kierunek siły, to i kierunek przyspieszenia będzie różny od kierunku siły. Jeśli zaś prędkość będzie się zbliżać do prędkości światła, to przyspieszenie będzie dążyć do zera. W rezultacie prędkość ciała nie będzie mogła osiągnąć prędkości światła, chociaż pęd będzie mógł wzrastać nieograniczenie. Widzimy jednak, że kiedy prędkość jest dużo mniejsza od prędkości światła, to masa jest bliska masie spoczynkowej i prawa ruchu Newtona są wystarczająco dobrze spełnione.

---

Energia kinetyczna Aby obliczyć relatywistyczną energię kinetyczną, rozważmy cząstkę o masie spoczynkowej $m_0$, będącą początkowo w spoczynku, przyspieszaną przez siłę o wartości F skierowaną wzdłuż osi x. Energia kinetyczna jest równa pracy wykonanej na drodze od $x=0$ do $x=x_k$, czyli całce z Fdx w granicach od zera do $x_k$. Podstawiamy wzór na siłę F i otrzymujemy całkę, którą łatwo obliczyć przez części.

---

Podstawiamy wzór na pęd, a iloczyn prędkości i jej pochodnej vdv przedstawiamy jako pochodną kwadratu prędkości.

---

Po scałkowaniu porządkujemy otrzymane wyrażenie.

---

Uwzględniając granice całkowania, otrzymujemy wzór na energię kinetyczną. Widzimy, że energia kinetyczna jest funkcją prędkości, którą możemy przedstawić jako różnicę między wyrażeniem zależnym od prędkości i wyrażeniem stałym. Narzuca się interpretacja, że energia kinetyczna jest różnicą między całkowitą energią cząstki poruszającej się z prędkością v i jej energią spoczynkową. Inaczej: energia całkowita jest sumą energii kinetycznej i spoczynkowej.

---

Otrzymaliśmy słynny wzór Einsteina wyrażający równoważność masy i energii. Zwróćmy uwagę, że czynnik $c^2$, przez który mnożymy masę jest wielką liczbą – dlatego niewielki nawet ubytek masy spoczynkowej powoduje wyzwolenie ogromnej energii. Dzieje się tak na przykład podczas rozszczepienia ciężkich jąder w reaktorze atomowym lub, w sposób niekontrolowany, w bombie atomowej. Możliwy jest też proces odwrotny - zamiana energii na masę. Gdy zderzają się cząstki pędzące z prędkościami bliskimi prędkości światła, ich energia kinetyczna ulega zamianie na masę nowych cząstek rodzących się w zderzeniu.

---

Dowodem słuszności związku wyrażającego równoważność masy i energii może być zdjęcie przedstawiające tory ponad 1000 cząstek wyprodukowanych w wyniku zderzenia dwóch jąder złota, których sumaryczna energia w układzie środka masy wynosiła 130 GeV (gigaelektronowoltów). Jądra przyspieszone były w specjalnym akceleratorze tzw. zderzaczu RHIC (Relativistic Heavy Ion Collider) w Brookhaven National Laboratory, w USA. Przed zderzeniem biegły w kierunku prostopadłym do płaszczyzny rysunku. W momencie zderzenia energia kinetyczna jąder zamienia się w masy tysięcy cząstek powstałych w zderzeniu, zgodnie ze wzorem: $E=m{c}^2$.

---

Sprawdźmy, czy dla małych prędkości wzór na energię kinetyczną przejdzie w klasyczne wyrażenie. Stosujemy rozwinięcie w szereg Taylora wokół punktu x = 0 (x =v/c) i pomijamy wyrazy wyższych rzędów. Otrzymujemy znany wzór na energię kinetyczną. Pamiętajmy jednak, że jest to wzór przybliżony, który można stosować tylko dla małych prędkości (małych w porównaniu z prędkością światła).

---

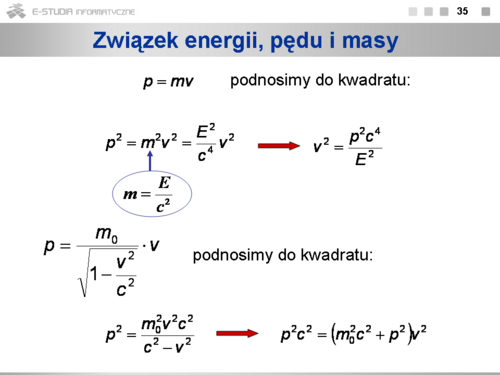
Związek energii, pędu i masy Aby znaleźć związek między pędem i energią, podnosimy stronami do kwadratu dwa równania wyrażające pęd $p=mv$ oraz .

---

Wstawiając kwadrat prędkości wyznaczony z pierwszego równania do drugiego, otrzymujemy związek energii całkowitej, pędu i masy spoczynkowej. Można ten związek przedstawić tak, aby po lewej stronie był kwadrat energii spoczynkowej, który jest jednakowy w każdym układzie odniesienia. Wynika z tego, że również wyrażenie po prawej stronie równania: $E^2-p^2{m}^2$ jest niezmiennikiem transformacji Lorentza.

---

Jeśli pęd wyrazimy przez współrzędne $p_x,p_y,p_z$ otrzymamy wyrażenie, które oznacza stałość w różnych układach odniesienia długości czterowektora o składowych określonych przez energię i składowe pędu. Czterowektor ten nazywa się czterowektorem energii-pędu.

---

Transformacja Lorentza pędu i energii Analogicznie do czterowektora czasoprzestrzennego konstruujemy czterowektor energii-pędu. Trzy współrzędne to składowe pędu $p_x,p_y,p_z$ , a czwarta współrzędna to energia podzielona przez prędkość światła E/c. Zwróćmy uwagę, że zarówno pęd jak i energia nie są niezmiennikami transformacji Lorentza, to znaczy, nie są jednakowe w każdym inercjalnym układzie odniesienia. To samo ciało może spoczywać w jednym układzie, a w innym poruszać się z wielką prędkością. Oczywiście w pierwszym układzie pęd będzie równy zeru, a energia równa energii spoczynkowej, a w drugim pęd różny od zera a energia równa sumie energii spoczynkowej i kinetycznej. Natomiast długość czterowektora energii- pędu jest jednakowa we wszystkich układach inercjalnych.

---

Czterowektor energii-pędu jest analogiczny do czterowektora czasoprzestrzennego. Dlatego transformacja Lorentza pędu i energii ma podobną postać do transformacji współrzędnych i czasu.

---

Podsumowanie

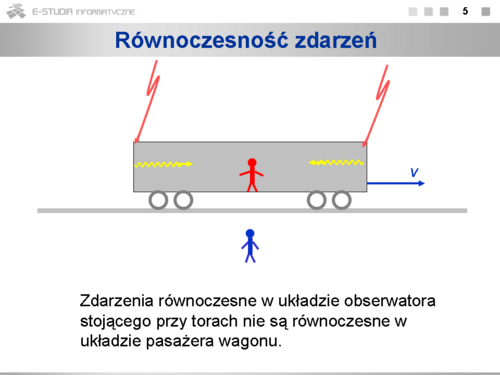
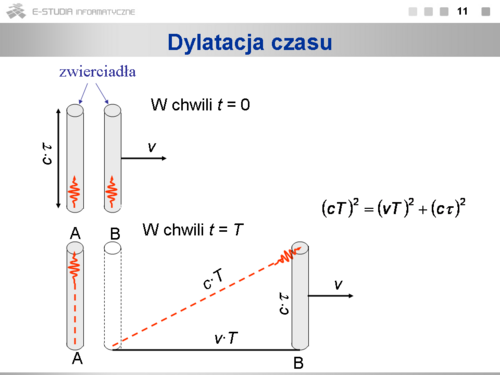
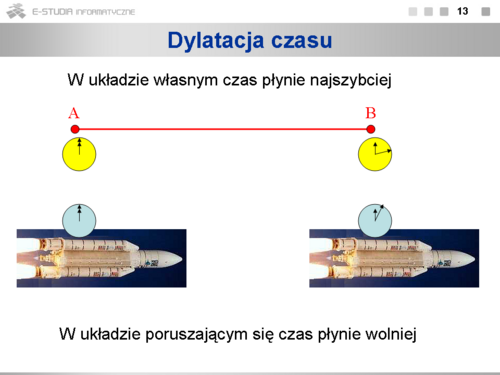
Wszystkie prawa relatywistyczne wynikają z dwóch postulatów Einsteina, które mówią, że po pierwsze prawa przyrody są takie same we wszystkich inercjalnych układach odniesienia, a po drugie, że prędkość światła w próżni jest jednakowa we wszystkich inercjalnych układach odniesienia i nie zależy od ruchu źródeł i odbiorników światła.Aby postulaty te były spełnione, trzeba transformację Galileusza zastąpić transformacją Lorentza. Jej konsekwencją jest dylatacja czasu, czyli spowolnienie wszelkich procesów w układzie poruszającym się względem obserwatora, a także kontrakcja długości, czyli skrócenie poruszającego się względem obserwatora pręta. Zdarzenia jednoczesne w jednym układzie nie muszą być jednoczesne w innym.

Jeśli pęd zdefiniujemy jako $\overrightarrow{p}=m\cdot \gamma \overrightarrow{v}$ i energię jako $E=m\cdot \gamma \cdot c^2$ ,gdzie $\gamma ={(1-v^2/c^2)}^{-1/2}$ to pęd i energia są zachowane we wszystkich układach inercjalnych, jeśli są zachowane w jakimkolwiek układzie. Ciało pozostające w spoczynku ma energię spoczynkową $E=m\cdot c^2$ i w pewnych procesach energia ta może być zamieniona na inne formy energii, na przykład na energię kinetyczną. Masa relatywistyczna ciała o prędkości v wyraża się wzorem:

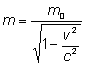Prędkość światła jest graniczną prędkością: żadne ciało o różnej od zera masie spoczynkowej nie osiągnie tej prędkości. Związek między energią całkowitą E, pędem p i masą spoczynkową m ma postać: $E^2=p^2{c}^2+(m{c}^2{)}^2$ .

---

Materiały do ćwiczeń

Zadanie 1

Na spoczywającą cząstkę o masie $m_0$ zaczyna działać stała siła. Jaką prędkość uzyska cząstka, gdy siła wykona pracę W? Czy cząstka porusza się ruchem jednostajnie zmiennym? Jaki interesujący wniosek wynika z porównania rozwiązania klasycznego i relatywistycznego?

Rozwiązanie

Energia kinetyczna cząstki jest równa pracy wykonanej przez siłę.

Rozwiązanie klasyczne

$\frac{1}{2}{m}_0{v}^2=W⟹v_{klas}=\sqrt{\frac{2W}{m_0}}$

Rozwiązanie relatywistyczne

$m{c}^2-m_0{c}^2=W$

$⟹$

Z porównania rozwiązań wynika, że wzór relatywistyczny przechodzi we wzór klasyczny, gdy spełniony jest warunek $W<<m_0{c}^2$ , a zatem gdy praca wykonywana przez siłę przyspieszającą jest znacznie mniejsza od energii spoczynkowej przyspieszanej cząstki. Wynika stąd, że obok znanego kryterium stosowania mechaniki relatywistycznej, gdy prędkość ciała jest bliska prędkości światła w próżni c, można sformułować drugie kryterium, które mówi, że mechanikę relatywistyczną stosujemy wtedy, gdy energia dostarczona ciału jest, co najmniej bliska jego energii spoczynkowej.

Odpowiedź: $v_{klas}=\sqrt{\frac{2W}{m_0}}$

$v_{rel.}=\sqrt{\frac{2W}{m_0}}\cdot \frac{\sqrt{1+(W/2m_0{c}^2)}}{1+(W/m_0{c}^2)}=v_{klas}\cdot \frac{\sqrt{1+(W/2m_0{c}^2)}}{1+(W/m_0{c}^2)}$

Mimo działania stałej siły cząstka porusza się ruchem zmiennym niejednostajnie. Przyspieszenie cząstki maleje, gdyż ze wzrostem prędkości rośnie masa cząstki. Przykład: Weźmy jako cząstkę elektron ( $m_0=9,1\cdot 10^{-31}kg$ , $e=1,6\cdot 10^{-19}C$ ) przyspieszany w polu elektrycznym (stałą siłą). Energię spoczynkową elektronu można obliczyć ze wzoru

$E_0=m_0{c}^2\approx 9,1\cdot 10^{-31}kg\cdot 9\cdot 10^{1}6m^2/s^2\approx 8,19\cdot 10^{-14}J\approx 0,51\cdot 10^{6}eV=0,51MeV$

(przypomnijmy, że używana w fizyce atomowej, relatywistycznej i jądrowej wygodna jednostka energii elektronowolt [eV] jest zdefiniowana jako energia, którą uzyskuje ładunek elementarny $e=1,6\cdot 10^{-19}C$ przebywając różnicę potencjałów U = 1 V, czyli $1eV=1,6\cdot 10^{-19}J$ )

Wskutek przebycia drogi, dla której różnica potencjałów wynosi U elektron uzyskuje energię kinetyczną równą pracy wykonanej przez pole elektryczne W = eU. Rozważmy dwa przypadki:

a) elektron przyspieszany w lampie kineskopowej w różnicy potencjałów $U_1=25kV$ uzyskuje energię

$W_1=e{U}_1=25keV$

zatem $\frac{W_1}{m_0{c}^2}\approx 0,05$ , $v_1=(v_{klas.}{)}_1\cdot \frac{\sqrt{1+0,025}}{1+0,05}\approx (v_{klas.}{)}_1\cdot 0,96$ , gdzie $(v_{klas.}{)}_1\approx 0,31c$

czyli różnica między wartością prędkości końcowej obliczoną klasycznie i relatywistycznie jest niewielka

b) elektron przyspieszany w akceleratorze van de Graaffa w różnicy potencjałów $U_2=25MV$ uzyskuje energię

$W_1=e{U}_2=25MeV$

zatem $\frac{W_1}{m_0{c}^2}\approx 50$ , $v_2=(v_{klas.}{)}_2\cdot \frac{\sqrt{1+250}}{1+5}\approx (v_{klas.}{)}_2\cdot 0,1$ , gdzie $(v_{klas.}{)}_2\approx 0,99c$

W tym przypadku wartość prędkości końcowej obliczona ze wzoru klasycznego jest oczywiście nonsensowna.

Odpowiedź: $T=2\pi \sqrt{\frac{m}{k_1+k_2}}$

---

Zadanie 2.

Cząstka o masie spoczynkowej $m_0$ porusza się z taką prędkością, że jej czas życia obserwowany w układzie laboratorium jest trzy razy dłuższy niż średni czas życia tej cząstki zmierzony wtedy, gdy cząstka jest w spoczynku. Oblicz energię kinetyczną tej cząstki i jej pęd.

Rozwiązanie

podstawiamy , więc $t=\tau \gamma$ , $\gamma =3$

Energia kinetyczna:

$E_k=m{c}^2-m_0{c}^2=m_0{c}^2(\gamma -1)=2m_0{c}^2$

Pęd:

$p^2{c}^2=E^2-{m^2}_0{c}^4=(m_0{c}^2\gamma {)}^2-{m^2}_0{c}^4={m^2}_0{c}^4({\gamma }^2-1)$

$p=2\sqrt{2}{m}_{0}c$

---

Zadanie 3

Jaka jest prędkość protonu, którego całkowita energia $E=100\cdot m_p{c}^2$ ? $m_p$ – masa spoczynkowa protonu.

Odpowidź

$v=0,9999995c$

---

Zadanie 4

Dwie cząstki lecą naprzeciwko siebie każda z prędkością 0,8c w układzie laboratorium. Jaka jest prędkość pierwszej cząstki obserwowana w układzie związanym z drugą cząstką?

Odpowidź

${v_1}^{\prime }=0,976c$

---

Zadanie 5

Jeśli zdefiniujemy gęstość jako masę relatywistyczną podzieloną przez objętość, to ile razy wzrośnie gęstość ciała, gdy porusza się ono z prędkością v?

Odpowidź

Gęstość wzrośnie n razy, gdzie: $n=\frac{1}{1-\frac{v^2}{c^2}}$

---

Słowa kluczowe

Inercjalny układ odniesienia

Prędkość światła

Postulaty Einsteina

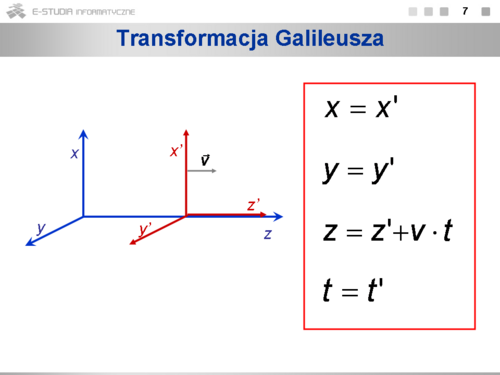
Transformacja Galileusza

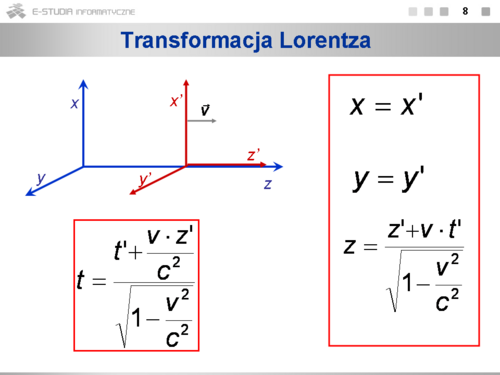
Transformacja Lorentza

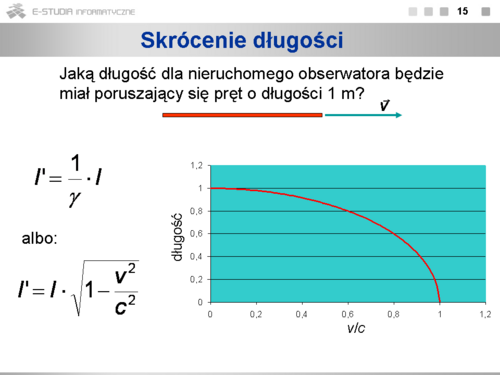
Kontrakcja (skrócenie) długości

Dylatacja czasu

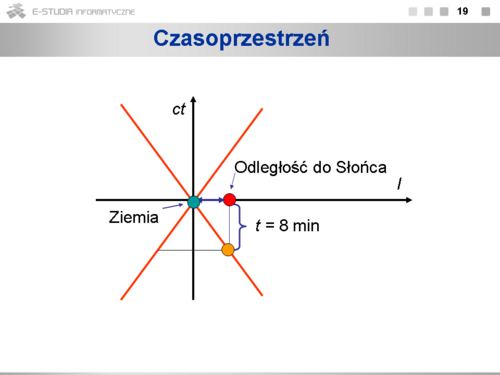
Czasoprzestrzeń

Interwał czasoprzestrzenny

Stożek świetlny

Linia świata

Czterowektor czasoprzestrzenny

Transformacja prędkości

Masa relatywistyczna

Pęd relatywistyczny

Energia całkowita

Energia spoczynkowa

Czterowektor energii-pędu

---

Bibliografia

1. J. Orear, Fizyka, WNT, Warszawa (1998);
2. R. Resnick, D. Halliday, Fizyka 1, PWN, Warszawa (1994);
3. I.W. Sawieliew, Wykłady z fizyki, PWN, Warszawa (1994).

---