PF Moduł 12

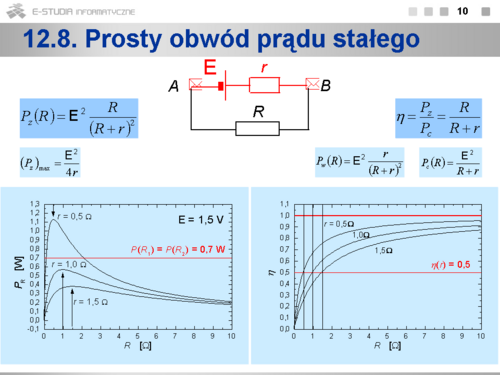
Podstawy fizyki - Elektromagnetyzm Wykład 12 - Prąd elektryczny 12.1. Natężenie i gęstość prądu 12.2. Prawo Ohma 12.3. Opór elektryczny 12.4. Mikroskopowy opis prądu elektrycznego 12.5. Praca i moc 12.6. Siła elektromotoryczna 12.7. Prawa Kirchhoffa 12.8. Prosty obwód prądu stałego 12.9-13. Materiały do ćwiczeń

---

12.1 Natężenie i gęstość prądu elektrycznego. Prąd elektryczny to uporządkowany ruch ładunków elektrycznych pod wpływem pola elektrycznego. Nośnikami prądu mogą być ładunki dodatnie (np. jony w cieczy lub w gazie) i ładunki ujemne (elektrony w ciele stałym, elektrony i jony w cieczy lub w gazie). Jako kierunek prądu przyjęto kierunek ruchu nośników dodatnich, a więc prąd płynie od potencjału wyższego do potencjału niższego. Natężenie prądu jest określone jako szybkość przepływu ładunku, czyli stosunek ładunku $dq$ przepływającego przez przekrój poprzeczny przewodnika w czasie $dt$, do tego czasu Jeśli w przepływie prądu uczestniczą różne nośniki ładunku, to natężenia prądu tych nośników dodają się. Gęstość prądu jest wektorem, którego kierunek jest zgodny z kierunkiem przepływu prądu, zaś wartość jest określona przez stosunek natężenia prądu $dI$ przepływającego przez mały element powierzchni przekroju poprzecznego przewodnika $d{S}_{\perp }$ do pola powierzchni tego elementu. Zatem $\overrightarrow{j}=j\overrightarrow{w}$ , gdzie $\overrightarrow{w}$ jest wersorem wskazującym kierunek ruchu dodatnich nośników prądu przez powierzchnię $d{S}_{\perp }$. Natężenie prądu jest strumieniem wektora gęstości prądu przez daną powierzchnię.

---

12.2 Prawo Ohma. Dla danego przewodnika stosunek napięcia między końcami przewodnika do natężenia prądu płynącego przez przewodnik jest wielkością stałą. Wielkość tę nazywamy oporem elektrycznym. Z prawa tego wynika, że dla przewodnika natężenie prądu jest liniową funkcją napięcia, współczynnik kierunkowy prostej $I(U)$ jest równy odwrotności oporu. Istnieją elementy przewodzące prąd dla których natężenie prądu nie jest liniową funkcją napięcia.

---

12.3 Opór elektryczny Opór elektryczny jednorodnego przewodnika o stałym przekroju jest zależny od jego długości $l$ i pola przekroju $S$ oraz od rodzaju przewodnika, gdzie $\rho$ to opór właściwy substancji, z której wykonany jest przewodnik. Wartość oporu właściwego silnie zależy od własności mikroskopowych substancji, z których wynika rodzaj nośników prądu (ładunek i masa) oraz ich koncentracja (liczba nośników w jednostce objętości). W przewodnikach (metalach) nośnikami są elektrony. Ich koncentracja jest duża, tego rzędu co koncentracja atomów, stąd małe wartości oporu właściwego. Opór właściwy metali rośnie wraz ze wzrostem temperatury. Wg. najprostszego modelu zależność ta ma charakter liniowy, gdzie $\alpha$ jest temperaturowym współczynnikiem oporu. W izolatorach (dielektrykach) koncentracja nośników jest mała, stąd duże wartości oporu właściwego. W cieczach i w gazach duże wartości oporu właściwego wynikają nie tylko z małej koncentracji, ale również z małej ruchliwości nośników (duża masa jonów). W półprzewodnikach samoistnych (np. german, krzem) koncentracja nośników (elektrony i dziury) rośnie ze wzrostem temperatury, co prowadzi do zmniejszania wartości oporu właściwego. Silny wpływ na koncentrację nośników mają domieszki. Przewodnictwo właściwe $\sigma$ to odwrotność oporu właściwego $\rho$.

---

12.4 Mikroskopowy opis przepływu prądu elektrycznego w przewodniku. W jednorodnym przewodzie o przekroju $S$ i koncentracji elektronów $n$ pole elektryczne działa na elektrony siłą $\overrightarrow{F}=-e\overrightarrow{E}$ , zmuszając je do określonego ruchu. Natężenie prądu można wyznaczyć licząc ile elektronów przepłynie w czasie $dt$ przez wybrany przekrój przewodu. Prowadzi to do wzorów określających natężenie prądu i powierzchniową gęstość prądu, gdzie $n$ jest koncentracją elektronów (liczba elektronów w jednostce objętości przewodnika), $e$ - ładunkiem elementarnym, zaś $u$ - prędkością unoszenia elektronów w kierunku wymuszonym przez pole elektryczne. Wzór określający zależność gęstości prądu od natężenia pola elektrycznego jest równoważny prawu Ohma. Poruszając się w kierunku wymuszonym przez pole elektryczne elektrony nie rezygnują z bezładnego ruchu cieplnego. Według prostego modelu klasycznego „gaz” elektronowy opisujemy podobnie jak gaz doskonały. Oznaczmy przez v średnią prędkość ruchu cieplnego elektronów w przewodniku, a przez $u$ średnią prędkość unoszenia elektronów w tym przewodniku, gdy płynie w nim prąd stały. Przewodnik znajduje się w temperaturze pokojowej. Wartość prędkości średniej ruchu cieplnego można oszacować wykorzystując wzory: $\begin{array}{ccc}\frac{1}{2}m⟨v^2⟩& ⟹& (v{)}_{\acute{s}r.kw.}=\sqrt{\frac{3kT}{m}}\approx 10^{5}m/s\end{array}$ w temperaturze pokojowej wartość prędkości unoszenia elektronów można oszacować wykorzystując wzory $\begin{array}{ccc}I=neuS& ⟹& u=\frac{I}{neS}\approx 2\cdot 10^{-5}m/s\end{array}$ dla typowych wartości $I,n,S$: $I=1A$, grubość miedzianego przewodu $d=2mm$, $n=8,5\cdot 10^{28}/m3$ (każdy atom miedzi daje jeden elektron swobodny, zatem znając masę molową miedzi $\mu =63,5g/mol$, gęstość miedzi $\rho =8,96g/c{m}^3$ i liczbę Avogadro $N_A=6,02\cdot 1023/mol$ można obliczyć koncentrację elektronów $n$). Warto zauważyć, że prędkość elektronów będących nośnikami prądu jest niezwykle mała w porównaniu z prędkością ruchu cieplnego. Można powiedzieć, że prąd płynie bardzo wolno. Oczywiście sygnał, który nakazuje elektronom przewodnictwa płynąć w określonym kierunku rozchodzi się niezwykle szybko. Sygnałem tym jest pole elektryczne, które rozchodzi się z prędkością równą prędkości światła. Mogłoby się wydawać, że pod wpływem pola elektrycznego elektrony będą się poruszać ruchem jednostajnie zmiennym, z rosnącą liniowo prędkością. Jednak, po przebyciu drogi równej średniej odległości międzyatomowej, wskutek zderzeń z atomami, prędkość elektronów spada do zera i przyspieszanie zaczyna się od nowa. W krótkim czasie od włączenia pola elektrycznego ustala się równowaga dynamiczna. Szybkość dostarczania energii przez pole zrównuje się z szybkością strat energii w zderzeniach i ustala się wartość prędkości unoszenia elektronów (tak, jakby oprócz stałej siły elektrycznej działała równa jej wartość siły oporu). Z takiego modelu przepływu prądu w wynika wzrost energii wewnętrznej przewodnika (wzrost temperatury) oraz interpretacja fizyczna oporu elektrycznego i pracy prądu elektrycznego.

---

12.5 Praca i moc Praca $dW$ wykonana przez pole elektryczne na wymuszenie przepływu ładunku dq w czasie $dt$ powoduje wzrost energii wewnętrznej przewodnika (wzrost temperatury), a w konsekwencji do otoczenia może przepłynąć ciepło $dQ=dW$. Pracę wykonaną w czasie $t$ otrzymamy po zsumowaniu porcji $dW$, które w przypadku prądu o stałym natężeniu daje wartość $W=UIt$. Wykorzystując prawo Ohma wzór ten można przedstawić w trzech postaciach. Moc jest równa szybkości wykonywania pracy i może być przedstawiona za pomocą trzech wzorów. W zastosowaniach praktycznych należy do danej sytuacji dostosować odpowiednią postać wzoru. Np. jeśli ustalona jest wartość napięcia zasilania U, to zarówno praca jak i moc są tym większe im mniejszy jest opór.

---

12.6 Siła elektromotoryczna Siła elektromotoryczna jest różnicą potencjałów wytwarzaną przez źródło prądu, czyli urządzenie przetwarzające energię (chemiczną, mechaniczną, ...) na energię elektryczną. Jej wartość jest określona przez wydatek energetyczny źródła $dW$ na wymuszenie przepływu ładunku $dq$, przypadający na jednostkę ładunku. Większe znaczenie praktyczne ma określenie siły elektromotorycznej jako napięcia na zaciskach źródła, gdy prąd w obwodzie zawierającym źródło nie płynie. (Uwaga: nazwa siła elektromotoryczna jest myląca, wielkość ta ma charakter napięcia i jej jednostką jest wolt).

---

12.7 Prawa Kirchhoffa Prawa Kirchhoffa wynikają z zasady zachowania ładunku i podstawowych własności pola elektrycznego. Za pomocą praw Kirchhoffa uzyskujemy równania, z których można obliczyć natężenie prądu w każdej części obwodu elektrycznego oraz napięcie między dwoma dowolnymi punktami obwodu.

---

12.8 Prosty obwód prądu stałego Składa się w swojej podstawowej wersji ze źródła o sile elektromotorycznej $E$ i oporze wewnętrznym $r$ oraz obwodu zewnętrznego o oporze $R$. Natężenie prądu w obwodzie osiąga wartość największą dla $R=0$, jest to tzw. prąd zwarcia $I_z$. Napięcie na zaciskach źródła $U_{AB}$ dąży do wartości równej sile elektromotorycznej, gdy $R\to \mathrm{\infty }$ . Moc w oporniku zewnętrznym $R$ osiąga wartość największą dla $R=r$. Moc całkowita $P_c$ jest równa sumie mocy $P_z$ w obwodzie zewnętrznym i mocy $P_w$ wewnątrz źródła: $P_c(R)=P_z(R)+P_w(R)$ Sprawność jest określona jako stosunek mocy w oporniku zewnętrznym do mocy całkowitej. Na rysunkach zostały przedstawione przykładowe wykresy zależności natężenia prądu, napięcia na zaciskach źródła, mocy w obwodzie zewnętrznym i sprawności od wartości oporu zewnętrznego. Z charakteru zależności mocy w obwodzie zewnętrznym od wartości oporu zewnętrznego wynika, że określoną moc P można uzyskać dla dwóch różnych wartości oporu $R_1<r$ i $R_2>r$. Na podstawie wykresu zależności sprawności od oporu zewnętrznego można stwierdzić, że bardziej korzystny jest wybór oporu $R>r$, gdyż większa jest sprawność.

---

12.9 Materiały do ćwiczeń Obliczanie oporu zastępczego układu oporników Jeśli układ oporników podłączymy do źródła napięcia $U_0$ to popłynie prąd o natężeniu $I$. Opór zastępczy układu, to opór opornika, przez który po podłączeniu do takiego źródła popłynie prąd o takim samym natężeniu. Wynika stąd ogólna i uniwersalna metoda obliczania oporu zastępczego: należy obliczyć natężenie prądu, który popłynie do danego układu oporników po podłączeniu do źródła napięcia $U_0$. To natężenie prądu będzie proporcjonalne do napięcia, a współczynnik proporcjonalności to odwrotność oporu zastępczego układu $I=\frac{1}{R}\cdot U_0$ . Za pomocą tej metody można obliczyć opór dowolnego układu oporników, bez konieczności ustalania jak są połączone oporniki, a więc nawet bez znajomości wzorów na łączenie szeregowe, równoległe, łączenia w trójkąt i w gwiazdę, ... . Do obliczania natężenia prądu $I$ wykorzystywane są dwa podstawowe prawa fizyczne: zasada zachowania ładunku (czyli tzw. pierwsze prawo Kirchhoffa), w polu elektrostatycznym suma zmian potencjału na drodze zamkniętej jest równa zeru (czyli tzw. drugie prawo Kirchhoffa). Spośród różnych możliwych połączeń oporników wyróżniamy dwa podstawowe - połączenie szeregowe i połączenie równoległe. Szeregowe połączenie oporników. Oporniki uznajemy za połączone szeregowo, jeżeli płynie przez nie prąd o takim samym natężeniu. Układ $n$ oporników połączonych szeregowo można zastąpić opornikiem o oporze równym sumie ich oporów Równoległe połączenie oporników. Oporniki uznajemy za połączone równolegle, jeżeli napięcie na nich ma taką samą wartość. Układ $n$ oporników połączonych równolegle można zastąpić opornikiem o oporze, którego odwrotność jest równa sumie odwrotności ich oporów Układy oporników spotykane w zadaniach są często zagmatwane. Aby obliczyć opór takiego układu, staramy się narysować go w prostszy sposób, ustalając które oporniki są połączone szeregowo a które równolegle. Układ oporników można oczywiście przekształcać tylko w taki sposób, aby natężenia prądów płynących przez poszczególne oporniki nie uległy zmianie. Najczęściej stosowane są dwa sposoby: punkty o tym samym potencjale można połączyć, pojedynczy opornik można zastąpić dwoma opornikami, które następnie można rozłączyć. Przy analizie połączeń oporników należy zwracać uwagę na symetrię układu, która ułatwia np. dostrzeżenie punktów o tym samym potencjale.

---

12.10 Materiały do ćwiczeń Łączenie źródeł napięcia Podstawowe sposoby połączenia $n$ źródeł napięcia o sile elektromotorycznej $E$ i oporności wewnętrznej $r$ w baterię to połączenie szeregowe i połączenie równoległe. W przypadku połączenia szeregowego siła elektromotoryczna baterii jest sumą sił elektromotorycznych źródeł, opór wewnętrzny baterii jest sumą oporów wewnętrznych źródeł. W przypadku połączenia równoległego siła elektromotoryczna baterii jest równa sile elektromotorycznej pojedynczego źródła, opór wewnętrzny baterii wynika z połączenia równoległego oporów wewnętrznych źródeł. Maksymalna moc jaką można uzyskać w obwodzie zewnętrznym dołączonym do baterii jest niezależna od sposobu połączenia źródeł w baterię.

---