PF Moduł 12: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 135: | Linia 135: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M12_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M12_Slajd6.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''12.5 Praca i moc''' | ||
'''Praca''' <math>dW\,</math> wykonana przez pole elektryczne na wymuszenie przepływu ładunku <math>dq\,</math> w czasie <math>dt\,</math> | |||
:<math>\displaystyle dW=dq\cdot U=UIdt</math> | |||
powoduje wzrost energii wewnętrznej przewodnika (wzrost temperatury), a w konsekwencji do otoczenia może przepłynąć ciepło <math>dQ =dW</math>. | |||
Pracę wykonaną w czasie <math>t\,</math> otrzymamy po zsumowaniu porcji <math>dW\,</math>, które w przypadku prądu o stałym natężeniu daje wartość | |||
:<math>\displaystyle W=UIt</math> | |||
Wykorzystując prawo Ohma wzór ten można przedstawić w postaci | |||
:<math>\displaystyle W=RI^2t=\frac{U^2}{R}t</math> | |||
'''Moc''' jest równa szybkości wykonywania pracy | |||
:<math>\displaystyle P=\frac{dW}{dt}</math> | |||
i może być przedstawiona wzorami | |||
:<math>\displaystyle P=UI=RI^2\frac{U^2}{R}</math> | |||
|} | |} | ||
| Linia 143: | Linia 165: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M12_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M12_Slajd7.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''12.6 Siła elektromotoryczna ''' | ||
jest różnicą potencjałów wytwarzaną przez źródło prądu, czyli urządzenie przetwarzające energię (chemiczną, mechaniczną, ...) na energię elektryczną. Jej wartość jest określona przez wydatek energetyczny źródła <math>dW\,</math> na wymuszenie przepływu ładunku <math>dq\,</math>, przypadający na jednostkę ładunku, czyli | |||
:<math>\displaystyle E=\frac{dW}{dq}</math> | |||
Większe znaczenie praktyczne ma określenie siły elektromotorycznej jako napięcia na zaciskach źródła, gdy prąd w obwodzie zawierającym źródło nie płynie. | |||
(Uwaga: nazwa siła elektromotoryczna jest myląca, wielkość ta ma charakter napięcia i jej jednostką jest wolt). | |||
|} | |} | ||
| Linia 151: | Linia 181: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M12_Slajd8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M12_Slajd8.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''12.7 Prawa Kirchhoffa''' | ||
Prawa Kirchhoffa wynikają z zasady zachowania ładunku i podstawowych własności pola elektrycznego. Za pomocą praw Kirchhoffa uzyskujemy równania, z których można obliczyć natężenie prądu w każdej części obwodu elektrycznego oraz napięcie między dwoma dowolnymi punktami obwodu. | |||
|} | |} | ||
| Linia 159: | Linia 191: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M12_Slajd9.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M12_Slajd9.png|thumb|500px]] | ||
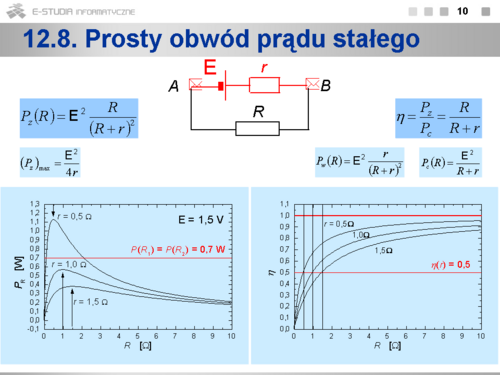
|valign="top"| | |valign="top"|'''12.8 Prosty obwód prądu stałego''' | ||
składa się w swojej podstawowej wersji ze źródła o sile elektromotorycznej <math>E\,</math> i oporze wewnętrznym <math>r\,</math> oraz obwodu zewnętrznego o oporze <math>R\,</math>. | |||
Natężenie prądu w obwodzie <math>\displaystyle I(R)=\frac{E}{R+r}</math> | |||
osiąga wartość największą dla <math>R = 0</math>, jest to tzw. prąd zwarcia <math>\displaystyle I_z=\frac{E}{R}</math> | |||
Napięcie na zaciskach źródła <math>U_{AB}\,</math> <math>\displaystyle U_{AB}E=\frac{R}{R+r}</math> | |||
dąży do wartości równej sile elektromotorycznej, gdy <math>R\to \infty\,</math>. | |||
Moc wydzielona w oporniku zewnętrznym <math>R\,</math> <math>\displaystyle P_z(R)=E^2\frac{R}{(R+r)^2}</math> | |||
osiąga dla <math>R = r</math> wartość największą <math>\displaystyle (P_z)_{max}=\frac{E^2}{4r}</math> | |||
Moc wydzielona na oporze wewnętrznym źródła <math>\displaystyle P_w(R)=E^2\frac{r}{(R+r)^2}</math> | |||
Moc całkowita wydzielona w obwodzie <math>\displaystyle P_c(R)=P_z(R)+P_w(R)=\frac{E^2}{R+r}</math> | |||
Sprawność jest określona jako stosunek mocy wydzielonej na oporniku zewnętrznym do mocy całkowitej i wynosi <math>\displaystyle \eta =\frac{P_z}{P_c}=\frac{R}{R+r}</math> | |||
Na rysunkach zostały przedstawione przykładowe wykresy zależności natężenia prądu, napięcia na zaciskach źródła, mocy wydzielonej na zewnątrz i sprawności od wartości oporu zewnętrznego. | |||
Z charakteru zależności mocy wydzielonej w obwodzie zewnętrznym od wartości oporu zewnętrznego wynika, że określoną moc P można uzyskać dla dwóch różnych wartości oporu <math>R_1<r\,</math> i <math>R2>r\,</math>. Na podstawie wykresu zależności sprawności od oporu zewnętrznego można stwierdzić, że bardziej korzystny jest wybór oporu <math>R > r\,</math>, gdyż większa jest sprawność. | |||
|} | |} | ||
Wersja z 12:33, 26 wrz 2006
 |
 |
 |
 |
 |








