PF Moduł 12: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 43: | Linia 43: | ||
'''Gęstość prądu''' jest wektorem, którego kierunek jest zgodny z kierunkiem przepływu prądu, zaś wartość jest określona wzorem | '''Gęstość prądu''' jest wektorem, którego kierunek jest zgodny z kierunkiem przepływu prądu, zaś wartość jest określona wzorem | ||
:<math>\displaystyle \overrightarrow{j}=\frac{dI}{dS_{\perp}}\overrightarrow{w}</math> | |||
gdzie <math>\dl\,</math> jest natężeniem prądu przepływającego przez mały element powierzchni przekroju poprzecznego przewodnika <math>dS_{\perp}\,</math> , a <math>\overrightarrow{w}\,</math> wersorem wskazującym kierunek ruchu dodatnich nośników prądu przez powierzchnię <math>dS_{\perp}\,</math>. Zatem natężenie prądu jest strumieniem wektora gęstości prądu przez daną powierzchnię, czyli | |||
:<math>\displaystyle I=\int_{S} \overrightarrow{j}\cdot \overrightarrow{S}</math> | |||
|} | |} | ||
| Linia 51: | Linia 55: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M12_Slajd3.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M12_Slajd3.png|thumb|500px]] | ||
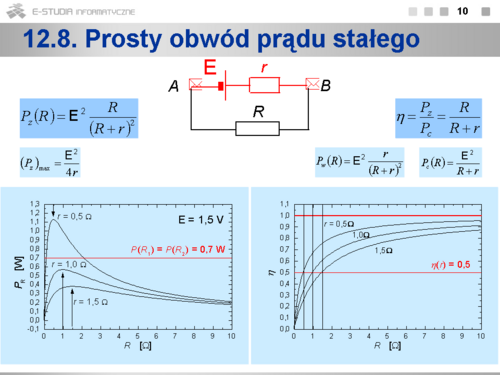
|valign="top"| | |valign="top"|'''12.2 Prawo Ohma.''' | ||
Dla danego przewodnika stosunek napięcia między końcami przewodnika do natężenia prądu płynącego przez przewodnik jest wielkością stałą. Wielkość tę nazywamy oporem elektrycznym | |||
:<math>\displaystyle \frac{U}{I}=const.=R</math> | |||
Z prawa tego wynika, że dla przewodnika natężenie prądu jest liniową funkcją napięcia, współczynnik kierunkowy prostej <math>I(U)\,</math> jest równy odwrotności oporu. | |||
Istnieją elementy przewodzące prąd dla których natężenie prądu nie jest liniową funkcją napięcia. | |||
|} | |} | ||
| Linia 59: | Linia 71: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M12_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M12_Slajd4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''12.3 Opór elektryczny''' | ||
'''Opór elektryczny''' dla jednorodnego przewodnika o stałym przekroju S i długości l jest określony wzorem | |||
:<math>\displaystyle R=\rho \frac{l}{S}</math> | |||
gdzie <math>\rho\,</math> to opór właściwy substancji, z której wykonany jest przewodnik. | |||
Wartość oporu właściwego silnie zależy od własności mikroskopowych substancji, z których wynika rodzaj nośników prądu (ładunek i masa) oraz ich koncentracja (liczba nośników w jednostce objętości). W przewodnikach (metalach) nośnikami są elektrony. Ich koncentracja jest duża, tego rzędu co koncentracja atomów, stąd małe wartości oporu właściwego. | |||
Opór właściwy metali rośnie wraz ze wzrostem temperatury. Wg. najprostszego modelu zależność ta ma charakter liniowy | |||
:<math>\displaystyle \rho(t)=\rho(t_0)\left[1+\alpha (t-t_0)\right]</math> | |||
gdzie <math>\alpha\,</math> jest temperaturowym współczynnikiem oporu. | |||
W izolatorach (dielektrykach) koncentracja nośników jest mała, stąd duże wartości oporu właściwego. | |||
W cieczach i w gazach duże wartości oporu właściwego wynikają nie tylko z małej koncentracji, ale również z małej ruchliwości nośników (duża masa jonów). | |||
W półprzewodnikach samoistnych (np. german, krzem) koncentracja nośników (elektrony i dziury) rośnie ze wzrostem temperatury, co prowadzi do zmniejszania wartości oporu właściwego. Silny wpływ na koncentrację nośników mają domieszki. | |||
'''Przewodnictwo właściwe''' to odwrotność oporu właściwego <math>\displaystyle \frac{1}{\rho}=\sigma</math> | |||
|} | |} | ||
| Linia 67: | Linia 101: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M12_Slajd5.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M12_Slajd5.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''12.4 Mikroskopowy opis przepływu prądu elektrycznego w przewodniku.''' | ||
W jednorodnym przewodzie o przekroju <math>S\,</math> i koncentracji elektronów <math>n\,</math> pole elektryczne działa na elektrony siłą <math>\displaystyle \overrightarrow{F}=-e\overrightarrow{E}</math> , zmuszając je do określonego ruchu. Natężenie prądu można wyznaczyć licząc ile elektronów przepłynie w czasie <math>dt\,</math> przez wybrany przekrój przewodu. Prowadzi do wzoru określającego natężenie prądu i powierzchniową gęstość prądu | |||
:<math>\begin{matrix} \displaystyle I=neuS & \displaystyle \overrightarrow{j}=ne\overrightarrow{u} \end{matrix}</math> | |||
gdzie <math>n\,</math> jest koncentracją elektronów (liczba elektronów w jednostce objętości przewodnika), <math>e\,</math> - ładunkiem elementarnym, zaś <math>u\,</math> - prędkością unoszenia elektronów w kierunku wymuszonym przez pole elektryczne. Wzór ten można następnie przekształcić do postaci | |||
|} | |} | ||
Wersja z 11:33, 26 wrz 2006
 |
 |
 |
 |
 |
 |
 |
 |
 |




