MO Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 276: | Linia 276: | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd34.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
*Zbieżność skończona, która ma miejsce wtedy gdy istnieje taka liczba K dla której x(K) = | *Zbieżność skończona, która ma miejsce wtedy gdy istnieje taka liczba K dla której <math>x(^{K)} = <math>x^o</math></math>. Z punktu widzenia znajdowania rozwiązań zadań optymalizacji wydaje się, że to najlepszy rodzaj zbieżności. Taki rodzaj zbieżności ma algorytm Simplex rozwiązywania zadań liniowych. Jednak jak pamiętamy, liczba iteracji może być bardzo duża, co oznacza, że na rozwiązanie zadania trzeba bardzo długo czekać. Metody punktu wewnętrznego nie mają skończonej zbieżności jednak dają zadowalające przybliżenie rozwiązania dużo szybciej. Dlatego wciąż trwają poszukiwania coraz bardziej skutecznych metod tego typu. A wniosek ogólny – z praktycznego punktu widzenia zbieżność skończona z bardzo dużym K może być gorsza niż zbieżność nieskończona, w sytuacji w której ciąg szybko zmierza do niewielkiego otoczenia rozwiązania. | ||
*Znana Państwu z analizy matematycznej zbieżność wektorowego ciągu nieskończonego, zwana jest w teorii metod optymalizacji krótko zbieżnością (nieskończoną). Jest ona rozumiana dwojako: jako zbieżność do rozwiązania <math>x^o</math>, albo dla funkcji gładkich – zbieżność do punktu stacjonarnego gradientu, tzn. takiego wektora <math>\hat{x}</math> , że | |||
<math>\nabla f (\hat{x})=0</math> | |||
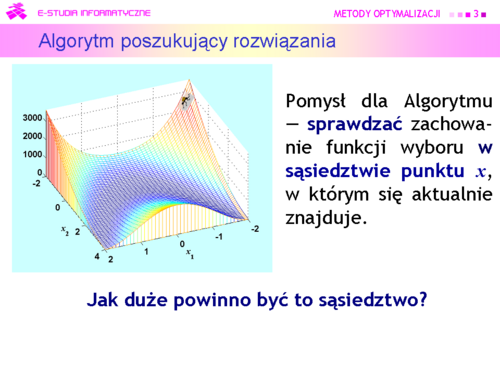
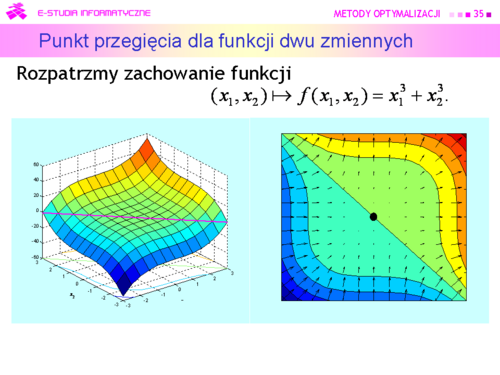
Jak pamiętamy punkt może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie. | Jak pamiętamy punkt może być punktem lokalnego minimum, maksimum albo lokalne zachowanie funkcji w różnych kierunkach może być różne, np. może to być punkt siodłowy albo punkt przegięcia. Ten ostatni przypadek pokazuje rysunek na następnej stronie. | ||
*Dlatego w niektórych wypadkach twórcom algorytmów udaje się udowodnić własność jeszcze słabszą: ciąg wektorów generowany przez algorytm zawiera podciąg zbieżny. | |||
Akceptacja zbieżności ostatniego rodzaju po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym “optymistycznym” podejściu do analizy sytuacji. | Akceptacja zbieżności ostatniego rodzaju po pokazaniu na przykładach, że algorytm w rozsądnej liczbie kroków (iteracji) znajduje dobre przybliżenie rozwiązania mieści się w przyjętym “optymistycznym” podejściu do analizy sytuacji. | ||
| Linia 288: | Linia 290: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd35.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd35.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|W tym przypadku rozwiązaniem równania <math>\nabla f (\hat{x})=0</math> jest <math>\hat{x}=(0,0)</math> , a ten punkt ekstremum, nawet lokalnym, dla rozważanej funkcji nie jest. Jednak nasze optymistyczne podejście pozwala przyjąć, że przypadki takie jak przedstawiony, są bardzo rzadkie. | ||
|} | |} | ||
---- | ---- | ||
| Linia 300: | Linia 302: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:MO_M5_Slajd37.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:MO_M5_Slajd37.png|thumb|500px]] | ||
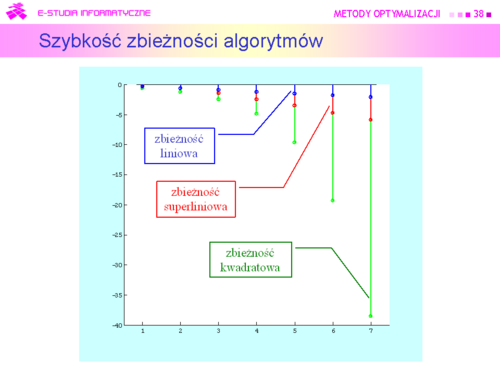
|valign="top"| | |valign="top"|Zbieżny ciąg <math>{x^{(k)}^\infty_{k=0}}</math> otrzymany w kolejnych krokach algorytmu, jest zbieżny | ||
a) liniowo, gdy dodatkowo | |||
<math>\frac{||x^{(k+1)-x^o}||}{||x^{(k)}-x^o||}\overrightarrow{k \rightarrow\infty}\rho\>0</math> | |||
|} | |} | ||
---- | ---- | ||
Wersja z 12:57, 25 wrz 2006
 |
 |
 |
 |
 |
Algorytm może być:
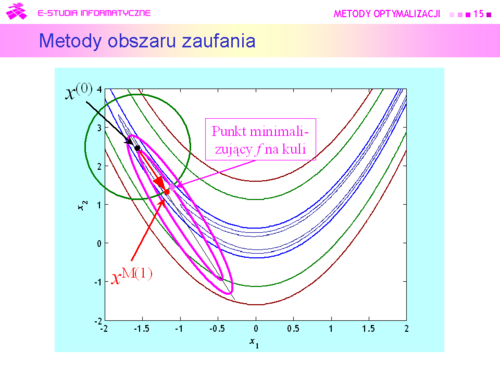
• ostrożny (wiem, że schody opadają w prawo, schodzę w prawo jeden stopień) –przyjąć xM(k) za środek nowego otoczenia
|
 |
 |
Większość algorytmów deterministycznych poszła w zapomnienie, ale do dzisiaj jest używany algorytm wymyślony przez:
J. A. Neldera i R. Meada i opublikowany w 1965 r. |
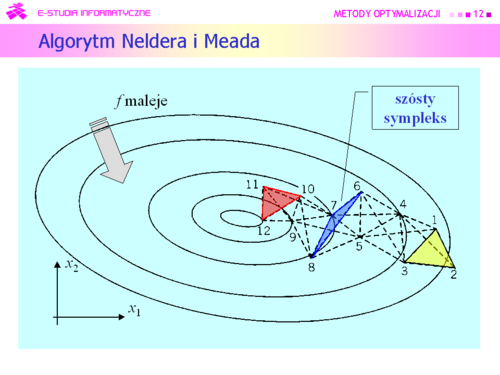 |
Dla funkcji kwadratowej algorytm Neldera i Meada zachowuje się bardzo ładnie. |
 |
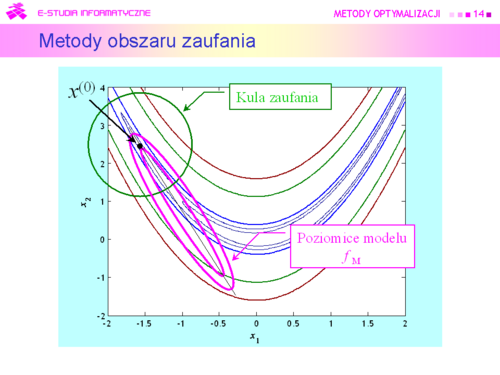
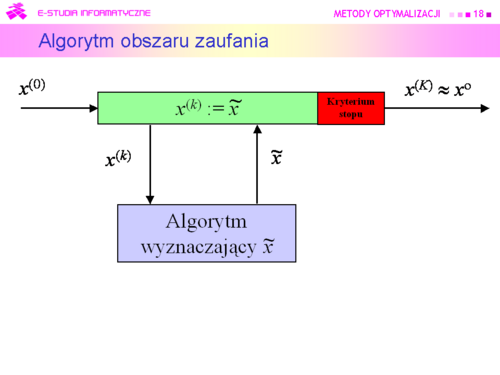
Metody oparte na takim rozumowaniu od połowy lat dziewięćdziesiątych XX w nazywa się:
Metodami obszaru zaufania (Trust region methods) |
 |
 |
 |
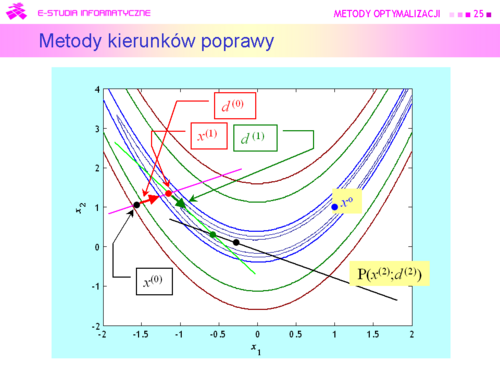
Tu oczywistym pomysłem jest wykorzystanie rozważań teoretycznych, pokazujących związek kierunku poprawy z gradientem (lemat 4.3).
Algorytm będzie zatem wykorzystywał: Metody kierunków poprawy |
 |
 |
 |
 |
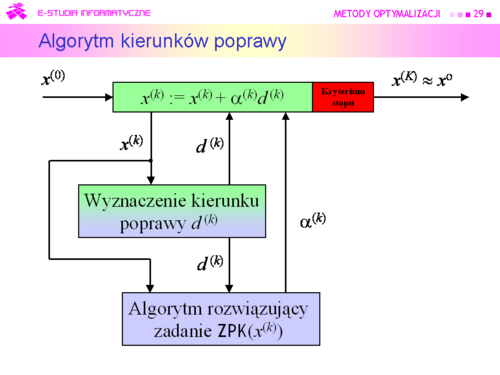
Teraz zauważmy tylko, że test stopu powinien zawierać dwa warunki: jeden badający “optymalność” kolejnego punktu, a drugi określający maksymalną liczbą iteracji. |
 |
 |
 |
 |
 |
 |
 |
 |