PF Moduł 14: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 459: | Linia 459: | ||
:<math>\displaystyle \overrightarrow{v}=\overrightarrow{\omega}\times\overrightarrow{r}</math> | :<math>\displaystyle \overrightarrow{v}=\overrightarrow{\omega}\times\overrightarrow{r}</math> | ||
<math>\displaystyle \overrightarrow{F}_m=-e(\overrightarrow{\omega}\times\overrightarrow{r})\times\overrightarrow{B}=e\overrightarrow{B}\times(\overrightarrow{\omega}\times\overrightarrow{r})=e[\overrightarrow{\omega}(\overrightarrow{B}\cdot\overrightarrow{r})-\overrightarrow{r}(\overrightarrow{B}\cdot\overrightarrow{\omega})]=-eB\omega\overrightarrow{r}</math> | :<math>\displaystyle \overrightarrow{F}_m=-e(\overrightarrow{\omega}\times\overrightarrow{r})\times\overrightarrow{B}=e\overrightarrow{B}\times(\overrightarrow{\omega}\times\overrightarrow{r})=e\left[\overrightarrow{\omega}(\overrightarrow{B}\cdot\overrightarrow{r})-\overrightarrow{r}(\overrightarrow{B}\cdot\overrightarrow{\omega})\right]=-eB\omega\overrightarrow{r}</math> | ||
która jest skierowana wzdłuż pręta w stronę punktu O. Wskutek przemieszczenia części elektronów w kierunku punktu O w pręcie powstaje pole elektryczne o natężeniu <math>\displaystyle \overrightarrow{F}_e=-e\overrightarrow{E}</math> , które na elektrony działa siłą | |||
Przemieszczanie elektronów ustaje, gdy w pręcie zostanie wytworzone pole elektryczne o takim natężeniu, że siły te zrównają się | |||
:<math>\begin{matrix} \displaystyle -eB\omega\overrightarrow{r}-e\overrightarrow{E}=0 & \displaystyle \overrightarrow{E}=-B\omega\overrightarrow{r} & \displaystyle E=-\frac{d\varphi}{dr} \end{matrix}</math> | |||
Znając natężenie pola elektrycznego możemy obliczyć różnicę potencjałów | |||
:<math>\begin{matrix} \displaystyle d\varphi =-Edr & \displaystyle \int_{\varphi_1}^{\varphi_2} d\varphi=\int_{0}^{l} B\omega rdr & \displaystyle \varphi_1-\varphi_2=-\frac{1}{2}B\omega l^2 & \displaystyle \varphi(l)-\varphi(0)=\frac{1}{2}B\omega l^2 \end{matrix}</math> | |||
Potencjał końca pręta jest większy niż potencjał w punkcie O. | |||
''Metoda 2'' | |||
Korzystając z prawa Faradaya można obliczyć siłę elektromotoryczną indukcji, a więc i różnicę potencjałów | |||
:<math>\begin{matrix} \displaystyle dE=-\frac{d\Phi_B}{dt}=-\frac{BdS}{dt}=-\frac{Bdrrd\alpha}{dt}=-B\omega rdr & \displaystyle E=-\int_{0}^{l} B\omega rdr=-\frac{1}{2}B\omega l^2 \end{matrix}</math> | |||
W układzie odniesienia związanym z wirującym prętem (nieinercjalny układ odniesienia) na elektrony działa siła bezwładności, która stara się przesunąć elektrony w kierunku końca pręta | |||
:<math>\displaystyle \overrightarrow{F}_b=m\omega^2 \overrightarrow{r}</math> | |||
Zrównanie się tej siły z siłą, jaką działa pole magnetyczne spowoduje, że napięcie między końcami pręta będzie równe zeru | |||
:<math>\begin{matrix} \displaystyle \overrightarrow{F}_b=m\omega^2 \overrightarrow{r}-eB\omega\overrightarrow{r}=0 & \displaystyle \omega=-\frac{e}{m}B \end{matrix}</math> | |||
Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa | |||
:<math>\displaystyle \omega_c=1,76\cdot 10^{11}s^{-1}</math> | |||
Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa | |||
:<math>\displaystyle v_k=\omega l=1,76\cdot 10^{11}m/s>c</math> | |||
większą od prędkości światła w próżni, co jak wiadomo nie jest możliwe. | |||
<hr width="100%"> | <hr width="100%"> | ||
{ | '''Przykład 14.2 - drgania elektromagnetyczne''' | ||
Do obwodu o oporze R, indukcyjności L i pojemności C dołączono źródło napięcia <math>\displaystyle U(t)=U_0 sin\omega t</math> . Znaleźć zależność od czasu napięcia na kondensatorze, natężenia prądu, napięcia na oporniku oraz napięcia na zwojnicy. | |||
'''Rozwiązanie''' | |||
W obwodzie zachodzą drgania wymuszone. Znając funkcję <math>q(t)\,</math> można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego. | |||
'''Napięcie na kondensatorze''' | |||
:<math>\displaystyle U_C(t)=\frac{q(t)}{C}=U(t)=U_{C0} sin(\omega t-\varphi)</math> | |||
:<math>\begin{matrix} \displaystyle U_{C0}=U_0\frac{\omega_{0}^2}{\sqrt{(\omega_{0}^2-\omega^2)^2}+4\beta^2\omega^2} & \displaystyle \varphi=arctg\frac{2\beta \omega}{\omega_{0}^2-\omega^2} \end{matrix}</math> | |||
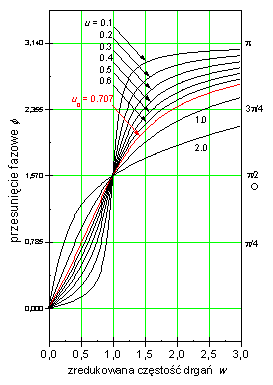
Zależność amplitudy napięcia na kondensatorze od częstości wymuszania jest oczywiście taka sama jak amplitudy ładunku. Napięcie na kondensatorze jest zgodne w fazie z ładunkiem, a więc <math>\varphi\,</math> określa również jego przesunięcie fazowe względem napięcia wymuszającego. | |||
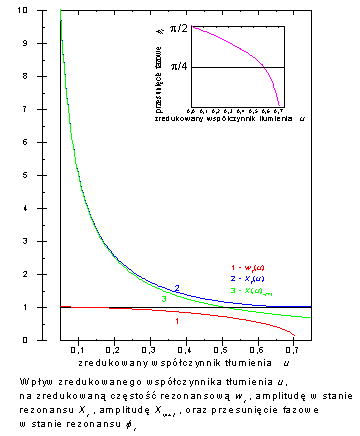
W stanie rezonansu, czyli dla częstości wymuszania równej <math>\omega_r\,</math>, amplituda napięcia na kondensatorze osiąga wartość maksymalną: | |||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 485: | Linia 534: | ||
|valign="top"| | |valign="top"| | ||
|}< | |} | ||
<hr width="100%"> | |||
Wersja z 23:11, 25 wrz 2006
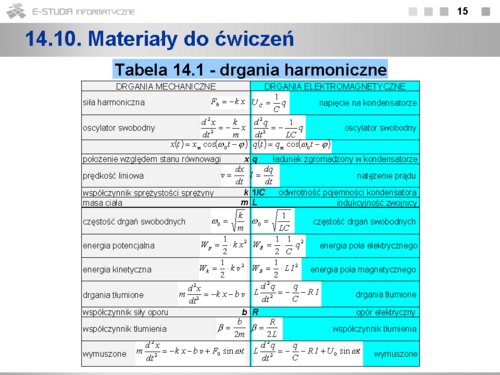
Materiały do ćwiczeń
Przykład 14.1 - indukcja elektromagnetyczna
Przewodzący pręt o długości wiruje z prędkością kątową wokół osi OY prostopadłej do pręta i przechodzącej przez jego koniec, w stałym, jednorodnym polu magnetycznym o wektorze indukcji .
Obliczyć wartość napięcia między końcami pręta i określić jego polaryzację.
Przyjąć, że , , .
Czy można tak dobrać wartość , aby w układzie odniesienia związanym z prętem konkurencja między siłą bezwładności i siłą jaką na elektrony działa pole magnetyczne spowodowała, że napięcie między końcami pręta będzie równe zeru?
Rozwiązanie
Metoda 1
Na elektrony w poruszającym się pręcie pole magnetyczne działa siłą
która jest skierowana wzdłuż pręta w stronę punktu O. Wskutek przemieszczenia części elektronów w kierunku punktu O w pręcie powstaje pole elektryczne o natężeniu , które na elektrony działa siłą
Przemieszczanie elektronów ustaje, gdy w pręcie zostanie wytworzone pole elektryczne o takim natężeniu, że siły te zrównają się
Znając natężenie pola elektrycznego możemy obliczyć różnicę potencjałów
Potencjał końca pręta jest większy niż potencjał w punkcie O.
Metoda 2
Korzystając z prawa Faradaya można obliczyć siłę elektromotoryczną indukcji, a więc i różnicę potencjałów
W układzie odniesienia związanym z wirującym prętem (nieinercjalny układ odniesienia) na elektrony działa siła bezwładności, która stara się przesunąć elektrony w kierunku końca pręta
Zrównanie się tej siły z siłą, jaką działa pole magnetyczne spowoduje, że napięcie między końcami pręta będzie równe zeru
Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa
Jak widać może to nastąpić przy częstości równej częstości cyklotronowej dla elektronu w polu o danej wartości wektora indukcji, która w tym przypadku jest równa
większą od prędkości światła w próżni, co jak wiadomo nie jest możliwe.
Przykład 14.2 - drgania elektromagnetyczne
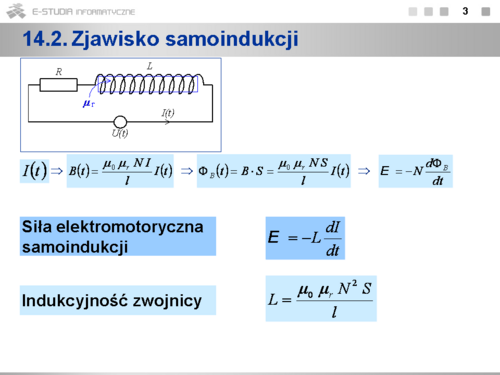
Do obwodu o oporze R, indukcyjności L i pojemności C dołączono źródło napięcia . Znaleźć zależność od czasu napięcia na kondensatorze, natężenia prądu, napięcia na oporniku oraz napięcia na zwojnicy.
Rozwiązanie
W obwodzie zachodzą drgania wymuszone. Znając funkcję można wyznaczyć pozostałe funkcje opisujące stan fizyczny układu drgającego.
Napięcie na kondensatorze
Zależność amplitudy napięcia na kondensatorze od częstości wymuszania jest oczywiście taka sama jak amplitudy ładunku. Napięcie na kondensatorze jest zgodne w fazie z ładunkiem, a więc określa również jego przesunięcie fazowe względem napięcia wymuszającego.
W stanie rezonansu, czyli dla częstości wymuszania równej , amplituda napięcia na kondensatorze osiąga wartość maksymalną:
 |
 |