PF Moduł 14

Wykład 14 - Zjawiska elektromagnetyczne 14.1. Zjawisko indukcji elektromagnetycznej 14.2. Zjawisko samoindukcji 14.3 Energia pola magnetycznego 14.4. Elektromagnetyczne drgania swobodne 14.5. Elektromagnetyczne drgania tłumione 14.6. Elektromagnetyczne drgania wymuszone 14.7. Równania Maxwella w postaci całkowej 14.8. Operatory różniczkowe 14.9. Równania Maxwella w postaci różniczkowej 14.10-13. Materiały do ćwiczeń

---

14.1 Zjawisko indukcji elektromagnetycznej Zjawisko indukcji elektromagnetycznej odkryte przez Michaela Faradaya (1791-1867) polega na wzbudzaniu w zamkniętym obwodzie prądu indukcyjnego, pod wpływem zmian strumienia zewnętrznego pola magnetycznego. Bezpośrednią przyczyną przepływu prądu indukcyjnego jest powstająca w obwodzie siła elektromotoryczna $E=-\frac{d{\mathrm{\Phi }}_B}{dt}$ Reguła Lenza, określająca kierunek prądu indukcyjnego, wynika przede wszystkim z zasady zachowania energii. Przepływ prądu indukcyjnego jest oznaką, że w obwodzie pojawiła się energia. Zatem zmiana strumienia magnetycznego wymaga wykonania pracy przez siłę zewnętrzną, która tę zmianę wywołuje. Np. zbliżanie magnesu skierowanego biegunem N w stronę obwodu zwiększa strumień magnetyczny przenikający przez powierzchnię obwodu. Prąd indukcyjny popłynie w takim kierunku, żeby wytworzone przez niego pole magnetyczne odpychało zbliżający się magnes, a więc przed obwodem musi powstać biegun N. Reguła Lenza wynika również z bardzo ogólnej reguły przekory (Le Chatelier i Braun), która głosi, że układy fizyczne zachowują się przekornie. Układ fizyczny znajdujący się w stanie równowagii poddany działaniu czynnika zewnętrznego reaguje tak, żeby zmniejszyć wpływ tego czynnika ii osiągnać nowy stan równowagi możliwie niezbyt odległy od stanu równowagi wyjściowej. Zjawisko indukcji elektromagnetycznej jest jednym z wielu zjawisk fizycznych, których przebieg wynika z reguły przekory.

---

14.2 Zjawisko samoindukcji Jeśli natężenie prądu płynącego w zwojnicy zmienia się w czasie $I(t)$ to funkcją czasu jest również wektor indukcji pola magnetycznego wytwarzanego przez ten prąd wewnątrz zwojnicy $B(t)=\frac{{\mu }_0{\mu }_{r}N}{l}I(t)$ oraz wartość strumienia magnetycznego przez powierzchnię każdego zwoju ${\mathrm{\Phi }}_B(t)=B\cdot S=\frac{{\mu }_0{\mu }_{r}NS}{l}I(t)$ a więc w zwojach powstają jednakowe i zgodne siły elektromotoryczne o wartości $E_z=-\frac{d{\mathrm{\Phi }}_B}{dt}$ Zatem całkowita siła elektromotoryczna powstająca w zwojnicy $E=-N\frac{d{\mathrm{\Phi }}_B}{dt}$ Po podstawieniu i przekształceniu otrzymujemy wzór $E=-L\frac{dl}{dt}$ z którego wynika zależność wartości siły elektromotorycznej samoindukcji od szybkości zmiany natężenia prądu, oraz od indukcyjności zwojnicy $L=\frac{{\mu }_0{\mu }_r{N}^{2}S}{l}$ czyli współczynnika zależnego od parametrów zwojnicy, określającego zdolność zwojnicy do wytwarzania siły elektromotorycznej samoindukcji. Dużą wartość $L$ można uzyskać dla zwojnicy o dużej liczbie zwojów, z rdzeniem ferromagnetycznym (duża wartość ${\mu }_r$). Zjawisko samoindukcji może zachodzić w każdym obwodzie, w którym płynie prąd o zmieniającym się w czasie natężeniu. Indukcyjność $L$ obwodu zależy od kształtu i rozmiarów obwodu oraz od obecności materiału ferromagnetycznego.

---

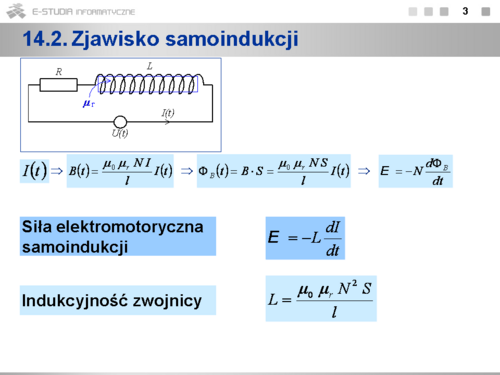
14.3 Energia pola magnetycznego W chwili $t_0=0$ zamykamy klucz i w obwodzie RL zaczyna płynąć prąd o rosnącym natężeniu, spełniającym równanie $U_0-L\frac{dI}{dt}-RI=0$ którego rozwiązaniem jest funkcja $I(t)\frac{U_0}{R}(1-e^{-(t/\tau )})$ gdzie $\tau$ jest stałą czasową procesu narastania natężenia prądu do wartości wynikającej z prawa Ohma. Pomnóżmy równanie opisujące przepływ prądu w obwodzie przez $I$ $U_{0}I=LI\frac{dI}{dt}+R{I}^2$ Iloczyn natężenia prądu i napięcia źródła $U_{0}I=P$ to moc źródła Składnik $R{I}^2=P_R$ to moc w oporniku. Zatem wyrażenie $LI\frac{dI}{dt}=P_B=\frac{d{W}_B}{dt}$ to moc w zwojnicy, czyli szybkość zmiany energii pola magnetycznego we wnętrzu zwojnicy. Po scałkowaniu otrzymujemy wzór określający energię pola magnetycznego wewnątrz zwojnicy $W_B=\frac{1}{2}L{I}^2$ Wykorzystując wzory $L=\frac{{\mu }_0{\mu }_r{N}^{2}S}{l}$ $B=\frac{{\mu }_0{\mu }_{r}N}{l}I$ otrzymamy zależność energii pola magnetycznego od wartości wektora indukcji magnetycznej $W_B=\frac{1}{2}\frac{1}{{\mu }_0{\mu }_r}{B}^{2}V$ gdzie $V$ jest objętością, oraz wzór określający przestrzenną gęstość energii pola magnetycznego $\frac{W_B}{V}=\frac{1}{2}\frac{1}{{\mu }_0{\mu }_r}{B}^2$ $w_B=\frac{1}{2}\overrightarrow{H}\cdot \overrightarrow{B}$

---

---

---

---

---

---

---

---

---

---

---