PF Moduł 11

---

11.1 Prawo Coulomba Dwa punktowe ładunki elektryczne $q_1$ i $q_2$ działają na siebie siłą, której wartość jest wprost proporcjonalna do iloczynu ładunków i odwrotnie proporcjonalna do kwadratu ich wzajemnej odległości: $\overrightarrow{F}=\frac{1}{4\pi {\epsilon }_0{\epsilon }_r}\cdot \frac{q_1{q}_2}{r^2}\cdot \frac{\overrightarrow{r}}{r}$ ${\epsilon }_0=8,85\cdot 10^{-12}\frac{C^2}{N{m}^2}$ gdzie ${\epsilon }_0$ jest przenikalnością elektryczną próżni zaś ${\epsilon }_r$ względną przenikalnością ośrodka. Ładunki różnoimienne przyciągają się, jednoimienne odpychają. Można udowodnić, że wzór ten określa również wartość siły, jaką działają na siebie jednorodne ładunki kuliste z odległości r większej od sumy ich promieni.

---

11.2 Opis dynamiczny pola elektrycznego Pole elektryczne wytworzone przez ładunki elektryczne to przestrzeń, w której na umieszczony ładunek działa siła elektryczna. Oddziaływaniu temu towarzyszy energia potencjalna zwana energią elektryczną. Opis pola elektrycznego powinien określać jego własności dynamiczne i energetyczne. Natężenie pola elektrycznego jest określone jako stosunek siły działającej w danym punkcie pola na punktowy ładunek próbny $q_0$ do wartości tego ładunku $\overrightarrow{F}=\frac{\overrightarrow{E}}{q_0}$ Wektor natężenia określa dynamiczne własności pola elektrycznego, co oznacza, że jeżeli znamy natężenie w danym punkcie pola, to siłę działającą na ładunek punktowy $q$ umieszczony w tym punkcie możemy obliczyć za pomocą wzoru $\overrightarrow{F}=q\cdot \overrightarrow{E}$ Linie sił pola elektrycznego to linie, do których styczny jest wektor siły, a więc i wektor natężenia pola. Zwrot linii sił pola jest określony przez zwrot wektora natężenia pola. Linie sił pola są w ogólności liniami krzywymi; w szczególnym przypadku, np. pola elektrycznego wytworzonego przez ładunek punktowy linie sił pola są liniami prostymi. Strumień wektora natężenia pola elektrycznego Porcję strumienia wektora natężenia pola elektrycznego przez mały element powierzchni dS (tak mały że może być traktowany jako płaski a natężenie pola w jego obrębie jest wektorem stałym) definiujemy jako: $d{\mathrm{\Phi }}_E=\overrightarrow{E}d\overrightarrow{S}=E\cdot S\cdot cos(\overrightarrow{E},d\overrightarrow{S})$ ${\mathrm{\Phi }}_E=\underset{S}{\int }\overrightarrow{E}d\overrightarrow{S}$ gdzie $d\overrightarrow{S}$ jest wektorem prostopadłym do tego elementu powierzchni, o wartości równej polu powierzchni $dS$. Wartość strumienia wektora natężenia pola elektrycznego przez całą powierzchnię $S$, którą obliczamy przez zsumowanie porcji strumienia przez poszczególne elementy powierzchni $dS$, jest równa liczbie linii sił pola przecinających tę powierzchnię. W najprostszym przypadku, gdy pole elektryczne jest jednorodne, strumień wektora natężenia pola elektrycznego przez płaszczyznę o powierzchni $S$ jest równy ${\mathrm{\Phi }}_E=EScos\alpha$ gdzie $\alpha$ jest kątem między wektorem natężenia pola elektrycznego i normalną do powierzchni. Prawo Gaussa dla wektora natężenia pola elektrycznego Strumień wektora natężenia pola elektrycznego przez zamkniętą powierzchnię ograniczającą układ ładunków wytwarzających pole elektryczne jest wprost proporcjonalny do sumarycznego ładunku układu $Q$ ${\mathrm{\Phi }}_E={\oint }_S\overrightarrow{E}d\overrightarrow{S}=\frac{1}{{\epsilon }_0{\epsilon }_r}Q$ $Q=\underset{V}{\int }\rho dV$ Współczynnik proporcjonalności jest tak dobrany, aby wyznaczony z prawa Gaussa wzór na natężenie pola elektrycznego wytworzonego przez ładunek punktowy $Q$ był zgodny ze wzorem wyznaczonym na podstawie prawa Coulomba. Prawo Gaussa wyraża bardzo ważną własność pola elektrycznego: jest to pole źródłowe. Źródłem pola jest ładunek. Ładunek dodatni jest dodatnim źródłem pola (linie sił pola wychodzą z ładunku dodatniego), ładunek ujemny jest ujemnym źródłem pola (linie sił pola wchodzą do ładunku ujemnego).

---

11.3 Opis energetyczny pola elektrycznego Praca Na ładunek punktowy q pole elektryczne o natężeniu $\overrightarrow{E}$ działa siłą $\overrightarrow{F}=q\cdot \overrightarrow{E}$ . Zatem praca przesunięcia ładunku z punktu $A$ do punktu $B$ jest określona wzorem: $W(A\to B)=-\underset{A}{\overset{B}{\int }}q\overrightarrow{E}d\overrightarrow{l}=q\underset{A}{\overset{B}{\int }}-\overrightarrow{E}d\overrightarrow{l}$ gdzie $d\overrightarrow{l}$ jest bardzo małym elementem krzywej wzdłuż której jest przesuwany ładunek. Można w prosty sposób wykazać, że wynik całkowania jest identyczny dla wszystkich krzywych łączących punkty $A$ i $B$. Oznacza to, że siła elektryczna jest siłą zachowawczą. Warto przypomnieć interpretację znaku pracy: praca dodatnia jest wykonana przez siły zewnętrzne, praca ujemna jest wykonana przez siły wewnętrzne, czyli przez układ fizyczny: pole - ładunek. Elektryczna energia potencjalna jest określona w następujący sposób: Wyobraźmy sobie przejście układu fizycznego oddziałującego siłami elektrycznymi od stanu fizycznego nr 1 do stanu fizycznego nr 2. Obydwu stanom przypisujemy elektryczną energię potencjalną, przy czym energia potencjalna układu w stanie drugim jest równa sumie energii potencjalnej w stanie pierwszym i pracy wykonanej przy przejściu od stanu do stanu $W_p(2)=W_p(1)+W(1\to 2)$ Praca wykonana przy przejściu od stanu nr 1 do stanu nr 2 spełnia w przypadku oddziaływań elektrycznych podstawowy warunek sensowności takiej definicji, tzn. jest niezależna od sposobu przejścia układu fizycznego od stanu początkowego do stanu końcowego (siły elektryczne są siłami zachowawczymi). Stan nr 1, czyli tzw. stan odniesienia można określić dwoma sposobami: Jako stan odniesienia wybieramy dowolny stan układu fizycznego i przypisujemy mu dowolną wartość energii (np. +100 J, -50 J, 0, ...); taki sposób jest często stosowany w zadaniach. Jako stan odniesienia wybieramy taki stan układu fizycznego, w którym siły elektryczne maleją do zera (odległość oddziałujących ładunków jest bardzo duża) i przypisujemy mu energię potencjalną równą zeru. Ten sposób określania energii potencjalnej jest często stosowany w teorii. Otrzymujemy wzory o charakterze ogólnym. Z takiego sposobu określania energii wynika, że energia potencjalna towarzysząca oddziaływaniom przyciągającym (ładunki różnoimienne) jest ujemna, zaś energia potencjalna towarzysząca oddziaływaniom odpychającym (ładunki jednoimienne) jest dodatnia. Potencjał elektryczny jest określony jako stosunek energii potencjalnej oddziaływania ładunku próbnego $+q_0$ z polem elektrycznym, w danym punkcie pola, do wartości tego ładunku $\phi =\frac{W_p}{+q_0}$ Potencjał elektryczny określa energetyczne własności pola elektrycznego, co oznacza, że jeżeli znamy potencjał w danym punkcie pola elektrycznego, to energię potencjalną oddziaływania pola z ładunkiem umieszczonym w tym punkcie możemy obliczyć ze wzoru $W_p=q\phi$ Ponieważ potencjał elektryczny jest określony za pomocą energii potencjalnej, to oczywiście ma on też charakter względny, a zatem potencjał elektryczny w danym punkcie pola jest równy sumie potencjału w punkcie odniesienia i pracy przeniesienia jednostkowego ładunku dodatniego z punktu odniesienia do danego punktu pola $\phi (2)=\phi (1)+\frac{W(1\to 2)}{+q_0}=\phi (1)-\underset{1}{\overset{2}{\int }}\overrightarrow{E}d\overrightarrow{l}$ przy czym słuszne pozostają uwagi dotyczące sposobu wyboru stanu odniesienia i wartości potencjału w tym stanie. Uwaga: W zadaniach, w których nie jest wyraźnie określony stan odniesienia i wartość potencjału w tym stanie, potencjał jest zwykle określany względem nieskończoności, gdzie przyjmujemy potencjał równy zeru. Powierzchnie ekwipotencjalne to powierzchnie, na których potencjał elektryczny ma stałą wartość. Powierzchnie ekwipotencjalne są prostopadłe do linii sił pola. Pracę przesunięcia ładunku punktowego $q$ w polu elektrycznym można wyrazić wzorem $W(1\to 2)=q[\phi (2)-\phi (1)]$

---

11.4 Ogólne własności pola elektrycznego wytworzonego przez ładunki Związek między natężeniem pola i potencjałem Natężenie pola i potencjał elektryczny zostały zdefiniowane w taki sposób, że zależą tylko od własności pola elektrycznego, które opisują, a nie od tego co w tym polu umieszczamy. Związek między wielkością wektorową, jaką jest natężenie pola, i wielkością skalarną, jaką jest potencjał, określono w następujący sposób: Jeżeli przesuwamy się wzdłuż linii sił pola, to wartość wektora natężenia pola jest równa szybkości zmiany potencjału, wziętej ze znakiem minus $E=-\frac{d\phi }{dr}$ gdzie dr jest bardzo małym przesunięciem. Minus oznacza, że zwrot wektora natężenia pola jest przeciwny do zwrotu przesunięcia przy którym potencjał rośnie. Linie sił pola są prostopadłe do powierzchni ekwipotencjalnych. Ogólny wzór określający związek między natężeniem pola i potencjałem można zapisać w postaci różniczkowej lub całkowej $\overrightarrow{E}=-grad\phi$ $\phi (2)=\phi (1)-\underset{1}{\overset{2}{\int }}\overrightarrow{E}d\overrightarrow{l}$ Ogólne własności: Pole elektryczne wytworzone przez ładunki to pole: źródłowe ${\oint }_S\overrightarrow{E}d\overrightarrow{S}=\frac{1}{{\epsilon }_0{\epsilon }_r}Q$ źródłem pola jest ładunek zachowawcze $W(A\to B)=-\underset{A}{\overset{B}{\int }}q\overrightarrow{E}d\overrightarrow{l}$ siła elektryczna jest siłą zachowawczą bezwirowe ${\oint }_L\overrightarrow{E}d\overrightarrow{l}=0$ linie sił pola mają początek i koniec, nie są krzywymi zamkniętymi

---

11.5 Dipol elektryczny Dipol elektryczny stanowią dwa ładunki różnoimienne $+q$ i $-q$ położone w odległości d. Układowi temu przypisujemy wektor elektrycznego momentu dipolowego określony wzorem ${\overrightarrow{p}}_e=q\overrightarrow{d}$ gdzie $\overrightarrow{d}$ jest wektorem skierowanym od ładunku ujemnego do dodatniego. Natężenie pola elektrycznego wytworzonego przez dipol w odległości $r$, dużej w porównaniu z ramieniem dipola $d$, ma wartość określoną wzorem $E=\frac{p_e}{r^3}$ W zewnętrznym polu elektrycznym na dipol działa moment sił określony wzorem $\overrightarrow{M}={\overrightarrow{p}}_e\times \overrightarrow{E}$ Energia potencjalna oddziaływania dipola z zewnętrznym polem elektrycznym względem stanu, w którym ${\overrightarrow{p}}_e\perp \overrightarrow{E}$, wynosi $W_p=-{\overrightarrow{p}}_e\cdot \overrightarrow{E}$ Wartości momentu sił działającego na dipol i energii oddziaływania z zewnętrznym polem zestawiono w tabeli dla różnych wartości kąta $\alpha$ jaki tworzy wektor momentu dipolowego z wektorem natężenia zewnętrznego pola. kąt $\alpha$ $0$ $90^{\circ }$ $180^{\circ }$ $270^{\circ }$ moment sił $M$ $0$ $pE$ $0$ $-pE$ energia potencjalna $W_p$ $-pE$ minimum $0$ $+pE$ maksimum $0$ stan równowagi trwała - nietrwała - Z zestawienia tego wynika, że oddziaływanie z zewnętrznym polem elektrycznym dąży do ustawienia dipola tak, aby wektor momentu dipolowego był zgodny z wektorem natężenia pola, czyli w stanie równowagi trwałej.

---

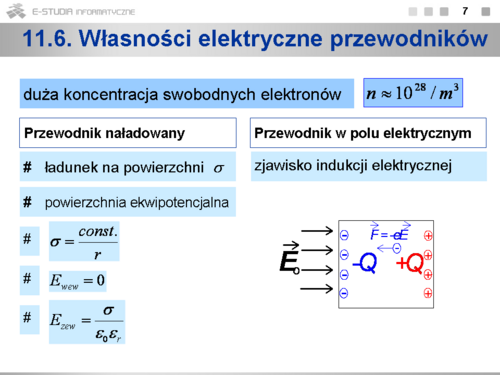
11.6 Własności elektryczne przewodników Przewodniki to ciała stałe o dużej koncentracji swobodnych elektronów (rzędu koncentracji atomów). Sumaryczny ładunek nienaładowanego przewodnika jest równy zero. Przewodnik naładowany W stanie równowagi ładunek gromadzi się na powierzchni przewodnika (swobodne ładunki jednoimienne w objętości przewodnika odpychają się i przemieszczają dotąd, dopóki nie znajdą się na powierzchni). W stanie równowagi powierzchnia naładowanego przewodnika jest powierzchnią ekwipotencjalną (ładunki przemieszczają się po powierzchni dopóty, dopóki potencjały wszystkich punktów nie wyrównają się, gdyby potencjały w dowolnych dwóch punktach były różne, następowałby między nimi przepływ ładunku). Rozkład gęstości powierzchniowej ładunku $\sigma$ jest zależny od kształtu przewodnika, gęstość powierzchniowa jest tym większa im mniejszy jest lokalny promień krzywizny powierzchni przewodnika. Natężenie pola elektrycznego wewnątrz przewodnika jest równe zeru (wynika to z prawa Gaussa). Natężenie pola elektrycznego na zewnątrz przewodnika, w pobliżu jego powierzchni jest wektorem prostopadłym do powierzchni i ma wartość $E=\frac{\sigma }{{\epsilon }_0}$ co wynika z prawa Gaussa.

---

---

---

---

---

---

---

---

---

---