PF Moduł 9

Wprowadzenie Z mikroskopowego punktu widzenia substancje mają budowę "ziarnistą". Składnikami ich są atomy bądź cząsteczki, których wzajemne oddziaływania określają własności makroskopowe substancji jak ciśnienie lub temperatura oraz stan skupienia: stały, ciekły lub gazowy. Ogromna liczba cząsteczek, z jaką zwykle mamy do czynienia uniemożliwia stosowanie do opisu ich ruchu równań Newtona w takim sensie, jak się to czyni w mechanice. W jednym centymetrze sześciennym gazu mieści się w warunkach normalnych około $10^{19}$ cząsteczek, które zderzają się ze sobą oraz ze ściankami naczynia. Do opisu ich ruchu stosuje się metody statystyczne, a wielkości makroskopowe charakteryzuje się poprzez uśrednione wartości wielkości mikroskopowych takich jak prędkości cząsteczek czy energie ich wzajemnego oddziaływania.

---

Czym jest ciśnienie gazu z mikroskopowego punktu widzenia? Ścianki naczynia zawierającego pewną porcję gazu uderzane są ustawicznie przez cząsteczki będące w chaotycznym ruchu. Wyznaczmy przekaz pędu przy takich zderzeniach. Dla uproszczenia przyjmijmy, że naczynie ma kształt sześcianu o długości ścianek równej $l$ .

---

W układzie współrzędnych prostokątnych rozważamy sprężyste zderzenie cząsteczki gazu, o wektorze prędkości $v$, ze ścianką naczynia prostopadłą do osi $X$. Prędkość cząsteczki zapiszemy w postaci wektora $\overrightarrow{v}=(v_x,v_y,v_z)$ Po odbiciu się od ścianki naczynia cząsteczka porusza się z prędkością $v^{\prime }$. W wyniku sprężystego zderzenia cząsteczki ze ścianką prostopadłą do osi $X$ zmieni znak tylko składowa prędkości wzdłuż tej osi, czyli będzie ${v^{\prime }}_x=-v_x$ , ${v^{\prime }}_y=v_y$ , ${v^{\prime }}_z=v_z$ Dalsze nasze rozważania dotyczyć będą tylko kierunku $X$ , stosować będziemy zapis skalarny.

---

Zmiana składowej pędu wzdłuż osi $X$ będzie różnicą pomiędzy pędem po i przed zderzeniem (Pęd oznaczamy tu dużą literą $P$ , bowiem małą litera oznaczać będziemy ciśnienie.) $\mathrm{\Delta }{P}_x=-m\cdot v_x-(m\cdot v_x)=-2m\cdot v_x$ Pęd przekazany ściance będzie odwrotnego znaku, a więc wyniesie $2m\cdot v_x$ .

---

Czas przelotu cząsteczki przez kostkę wynosi $t=l/v_x$ , zaś przelot w obie strony trwać będzie dwa razy dłużej; $\mathrm{\Delta }t=2\cdot l/v_x$ . Częstość $\nu$ uderzeń o ściankę, czyli liczba uderzeń w jednostce czasu będzie odwrotnością czasu przelotu cząsteczki w dwie strony, czyli $\nu =1/\mathrm{\Delta }t=v_x/(2\cdot l)$ . Pęd przekazany ściance w jednostce czasu równy będzie pędowi przekazanemu w jednym uderzeniu pomnożonemu przez liczbę uderzeń w jednostce czasu. $\frac{\mathrm{\Delta }{P}_x}{\mathrm{\Delta }t}=\frac{v_x}{2\cdot l}\cdot 2\cdot m\cdot v_x=\frac{m\cdot {v^2}_x}{l}$

---

Z drugiej zasady dynamiki wiemy, że $\mathrm{\Delta }P/\mathrm{\Delta }t=F$ . Pamiętamy też, że ciśnienie jest stosunkiem siły do powierzchni, na którą siła działa. Powierzchnia ta jest w naszym przypadku równa kwadratowi boku ścianki. Ciśnienie będące skutkiem uderzeń jednej cząsteczki w ściankę wynosi, więc $p=F/S=F/l^2$ . Sumując przyczynki od wszystkich uderzających w ściankę cząsteczek otrzymujemy wyrażenie na ciśnienie gazu działające na ściankę Założyliśmy tu, że wszystkie cząsteczki w liczbie $N$ mają tę samą masę $m$ . Długość ścianki w trzeciej potędze zamieniliśmy objętością sześcianu $V$ . Iloczyn masy cząsteczki m przez liczbę cząsteczek $N$ jest masą gazu w naczyniu, zaś podzielony przez objętość $V$ jest gęstością gazu, którą oznaczyliśmy symbolem $\rho$ . Symbol $⟨{v^2}_x⟩$ oznacza wartość średnią kwadratu składowej wektora prędkości wzdłuż osi $X$ .

---

Biorąc pod uwagę, że kwadrat wektora równy jest sumie kwadratów jego składowych ${\overrightarrow{v}}^2=v^2={v^2}_x+{v^2}_y+{v^2}_z$ i pamiętając, że wszystkie kierunki wektora prędkości są tak samo prawdopodobne oraz, że ruchy w każdym kierunku są niezależne - możemy zamienić wartość średnią kwadratu składowej przez wartość średnią kwadratu wektora prędkości, czyli $⟨{v^2}_x⟩=\frac{1}{3}⟨v^2⟩$ Ostatecznie otrzymujemy wzór wyrażający związek pomiędzy mikroskopowymi (średnia prędkość cząsteczek) i makroskopowymi (ciśnienie i gęstość) własnościami gazu $p=\frac{1}{3}\cdot \frac{m\cdot N}{V}\cdot ⟨v^2⟩=\frac{1}{3}\cdot \rho \cdot ⟨v^2⟩$ W naszych rozważaniach nie uwzględnialiśmy zderzeń pomiędzy cząsteczkami. Zwróćmy jednak uwagę, że w zderzeniach sprężystych jest zachowany pęd oraz energia kinetyczna, a więc przy dużej liczbie zderzających się cząsteczek zderzenia te nie będą wpływać na wartość średnią pędu przekazywanego ściankom naczynia. Wybraliśmy także regularny (sześcienny) kształt naczynia. W warunkach równowagi ciśnienie wywierane na wszystkie ścianki o dowolnym kształcie a także wewnątrz naczynia jest jednakowe, o czym wiemy z prawa Pascala. Rozważania nasze mają, więc ogólny charakter.

---

Dla znalezienia związku pomiędzy makroskopową i mikroskopową interpretacją temperatury pomnóżmy lewą i prawą stronę równania opisującego ciśnienie gazu przez objętość naczynia $V$ i porównajmy to wyrażenie z równaniem stanu gazu doskonałego $p\cdot V=\frac{1}{3}\cdot \rho ⟨v^2⟩\cdot V=\frac{1}{3}\cdot \begin{array}{c}{n}_M\cdot M\\ \overbrace{\rho \cdot V}\end{array}\cdot ⟨v^2⟩$ We wzorze tym iloczyn gęstości i objętości jest po prostu masą gazu, którą następnie wyraziliśmy w molach oznaczając przez $M$ jego masę molową.

---

Teraz masę gazu wyraziliśmy w molach, oznaczając przez $M$ jego masę molową. Mnożąc stronami przez $3/2$ i dzieląc przez liczbę Avogadro otrzymujemy $\frac{1}{2}\cdot \begin{array}{c}{m}_0\\ \overbrace{\frac{M}{N_A}}\end{array}\cdot ⟨v^2⟩=\frac{3}{2}\cdot \begin{array}{c}k\\ \overbrace{\frac{R}{N_A}}\end{array}\cdot T$ Zauważamy przy tym, że masa molowa podzielona przez liczbę Avogadro to po prostu masa jednej cząsteczki $m_0$ . Iloraz stałej gazowej i liczby Avogadro, to stała Boltzmanna $k$ . Stała ta ma sens stałej gazowej odniesionej do jednej cząsteczki. Jak zobaczymy, stała ta odgrywa fundamentalna rolę w fizyce. Wykorzystując wprowadzone oznaczenia możemy przepisać ostatnie równanie w postaci $\frac{1}{2}\cdot m_0\cdot ⟨v^2⟩=⟨\frac{1}{2}\cdot m_0\cdot v^2⟩=\frac{3}{2}\cdot k\cdot T$ Wyrażenie po lewej stronie jest wielkością mikroskopową - średnią energią kinetyczną chaotycznego ruchu cząsteczek gazu przypadającą na jedną cząsteczkę; wyrażenie po prawej stronie jest proporcjonalne do wielkości makroskopowej - temperatury bezwzględnej ciała.

---

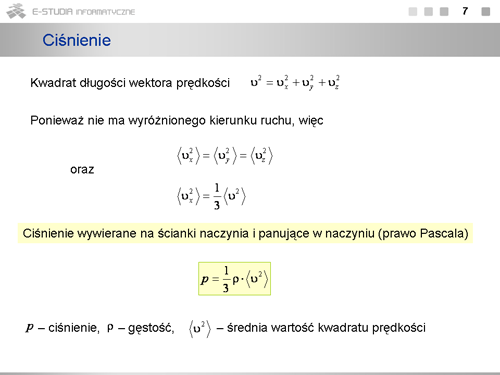
Stwierdzamy, więc temperatura jest miarą średniej energii kinetycznej chaotycznego ruchu cząsteczek. Średnia wartość kwadratu prędkości wynosi $⟨v^2⟩=\frac{3\cdot k\cdot T}{m_0}$ Na tej podstawie możemy określić tzw. średnią prędkość kwadratową definiując ją jako Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_{śr. kw.}=\sqrt{\left\langle v^2\right\rangle}=\sqrt{\frac{3\cdot k\cdot T}{m_0}}} Zauważmy, że możemy średnią prędkość kwadratową wyrazić poprzez wielkości makroskopowe: ciśnienie $p$ i gęstość gazu $\rho$ , bowiem również Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_{śr. kw.}=\sqrt{\frac{3\cdot p}{\rho}}} . Mamy, więc ideę prostego eksperymentu, za pomocą, którego określając łatwo mierzalne wielkości makroskopowe: $p$ (manometr) oraz objętość i masę gazu w celu wyznaczenia jego gęstości $\rho$ , możemy wyznaczyć statystycznie uśrednioną wielkość mikroskopową, jaką jest Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_{śr. kw.}\,} .

---

W naszych rozważaniach uwzględnialiśmy tylko energię ruchu postępowego cząsteczek. Jest to wystarczające, jeżeli rozpatrujemy gaz jednoatomowy - kiedy atomy możemy traktować jako punkty materialne. Do opisu ich położenia wystarczy podanie trzech współrzędnych. Cząsteczki wieloatomowe mogą wykonywać także ruch obrotowy; możliwe są również drgania atomów wchodzących w skład cząsteczki. Z ruchami tymi także wiąże się pewna energia (z obrotem - energia kinetyczna ruchu obrotowego, z drganiami - energia kinetyczna i energia potencjalna). Położenie punktu materialnego w przestrzeni jest w pełni opisane przez trzy współrzędne. Dwa połączone na sztywno punkty materialne mogą być opisane za pomocą pięciu (a nie sześciu) liczb, bowiem fakt ich sztywnego połączenia sprawia, że do opisu ich położenia wystarczy podać położenie jednego z nich oraz dwa kąty określające orientację w przestrzeni prostej łączącej te punkty. Położenie drugiego punktu na tej prostej jest znane, skoro znana jest ich wzajemna odległość. Położenie N niezależnych punktów materialnych wymaga jednak 3N liczb, skoro traktujemy te punkty jako niezależne. Położenie ciała sztywnego wymaga podania sześciu liczb. Pięć z nich określa, podobnie jak w przypadku układu dwóch ciał, położenie wybranego punktu, na przykład środka ciężkości, oraz kierunek wybranej prostej, na przykład osi obrotu. Punkty nie znajdujące się na osi mogą jednak zmieniać swe położenie wskutek ruch obrotowego wokół osi, potrzeba wiec jeszcze znać kąt obrotu - razem sześć liczb. Liczbę niezależnych wielkości za pomocą, których może być opisane położenie układu nazywamy liczbą stopni swobody układu. Liczba ta określa, możliwości ruchów, jakie może wykonywać cząsteczka. Z każdym ruchem wiąże się określona energia. Jeżeli ruch jest całkowicie chaotyczny i żaden rodzaj ruchu nie jest uprzywilejowany, to można przyjąć, że na każdy stopień swobody przypada jednakowa porcja energii. Stwierdzenie to jest treścią zasady ekwipartycji energii, czyli inaczej mówiąc, zasady równomiernego rozdziału energii na wszystkie stopnie swobody. Zasada ekwipartycji energii Na każdy stopień swobody cząsteczki przypada średnio ta sama energia. Jej wartość możemy określić na przykładzie ruchu postępowego cząsteczek punktowych. W tym przypadku liczba stopni swobody wynosi 3, a średnia energia kinetyczna cząsteczki, jest równa $3/2\cdot k\cdot T$ . Możemy uzupełnić ilościowo treść zasady ekwipartycji energii. Na każdy stopień swobody cząsteczki przypada średnio energia równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle kT/2\} . W oparciu o nasze rozważania widzimy, że energia ruchu cząsteczek w gazach wieloatomowych jest większa niż w gazach jednoatomowych.

---

Średnia energia cząsteczki o danej liczbie stopni swobody $i$ wynosi $⟨E⟩=\frac{i}{2}\cdot k\cdot T$ Dla $N$ cząsteczek gazu doskonałego, kiedy zaniedbuje się energię potencjalną wynikającą z sił wzajemnego oddziaływania cząsteczek, iloczyn $N⟨E⟩$ jest po prostu energią wewnętrzną gazu równą $U=N\cdot ⟨E⟩=N\cdot \frac{i}{2}\cdot k\cdot T$ Dla $n_M$ moli gazu doskonałego $U=n_M\cdot N_A\cdot \frac{i}{2}\cdot k\cdot T=n_M\cdot \frac{i}{2}\cdot k\cdot T$ Energię wewnętrzną układu $U$ utożsamiamy z całkowitą energia wszystkich cząsteczek. Ponieważ dla $n_M$ moli gazu doskonałego $dU=n_M\cdot C_V\cdot dT$ więc, otrzymujemy $C_V=\frac{1}{n_M}\cdot \frac{dU}{dT}=\frac{i}{2}\cdot R$ Wykorzystując wzór Mayera, $C_p-C_V=R$ $C_p=\frac{i+2}{2}\cdot R$ Za pomocą liczby stopni swobody cząsteczki gazu można też wyrazić wykładnik adiabaty $\kappa =\frac{C_p}{C_V}$ $\kappa =\frac{i+2}{i}$

---

Rezultatem chaotycznego ruchu cząsteczek są ich zderzenia następujące także w sposób chaotyczny. Od czego zależy liczba zderzeń cząsteczek? Jaką drogę cząsteczki przebiegają pomiędzy kolejnymi zderzeniami i od czego ta droga zależy? Trzeba pamiętać, że cząsteczki nie są "małymi kulami bilardowymi", że oddziałują ze sobą, zaś potencjał tego oddziaływania jest funkcją odległości pomiędzy nimi. Odległość największego zbliżenia można uznać za efektywną średnicę cząsteczki. Średnica ta zależna jest od energii cząsteczki, a średnia energia - od temperatury. Efektywne pole powierzchni, jakie cząsteczka stanowi w procesie wzajemnych zderzeń nazywa się przekrojem czynnym cząsteczki $\sigma =\pi \cdot d^2$ Średnia długość drogi, jaką przebywa cząsteczka w ciągu jednej sekundy równa jest, co do wartości, średniej prędkości cząsteczki $⟨v⟩$ . Jeśli w tym czasie cząsteczka zderzyła się $\nu$ razy, to jej średnia droga pomiędzy zderzeniami wynosi $\lambda =\frac{⟨v⟩}{\nu }$ Droga ta nosi nazwę średniej drogi swobodnej. Dla wyznaczenia średniej liczby zderzeń załóżmy chwilowo, że porusza się tylko jedna cząsteczka, zaś wszystkie pozostałe są nieruchome. Zderzenie z inną cząsteczką nastąpi wtedy, kiedy ta znajdzie się w obrębie walca, jaki wyznacza poruszająca się cząsteczka. Jest to swego rodzaju "rurka" o przekroju równym przekrojowi czynnemu i długości równej długości przebiegu cząsteczki w ciągu sekundy. Objętość tej rurki wynosi $\pi \cdot d^2\cdot ⟨v⟩$ . Liczbę cząsteczek w obrębie rurki uzyskamy mnożąc jej objętość przez liczbę cząsteczek w jednostce objętości $n$ . Liczba zderzeń z nieruchomymi cząsteczkami wyniosłaby wiec ${\nu }^{\prime }=\pi \cdot d^2\cdot ⟨v⟩\cdot n$ . Cząsteczki poruszają się jednak, a względna prędkość dwu cząsteczek równa jest ${\overrightarrow{v}}_{wzgl}={\overrightarrow{v}}_2-{\overrightarrow{v}}_1$ . Kwadrat tej prędkości względnej wynosi ${v^2}_{wzgl}=({\overrightarrow{v}}_2-{\overrightarrow{v}}_1{)}^2={v^2}_2+{v^2}_1-2\cdot {\overrightarrow{v}}_1\cdot {\overrightarrow{v}}_2$ . Dla wyznaczenia wartości średniej kwadratu prędkości względnej weźmy pod uwagę, że dla niezależnych wielkości średnia wartość sumy równa jest sumie wartości średnich oraz, że średnia iloczynu wektorów prędkości musi byś równa zeru. To ostatnie stwierdzenie wynika z faktu, że średnia wartość wektora prędkości, którego kierunki są chaotyczne, czyli dodatnie i ujemne z tym samym prawdopodobieństwem, musi, być równa zeru, zaś średnia iloczynu wielkości niezależnych jest iloczynem średnich. Mamy wiec $⟨{v^2}_{wzgl}⟩=⟨{v^2}_2⟩+⟨{v^2}_1⟩=2\cdot ⟨v^2⟩$ Dla średniej kwadratowej wartości prędkości względnej, a także dla proporcjonalnej do niej wartości średniej arytmetycznej mamy relację postaci $⟨{v^2}_{wzgl}⟩=\sqrt{2}\cdot ⟨v⟩$ Liczba zderzeń z uwzględnieniem wzajemnego ruchu cząsteczek jest, więc $\nu =\sqrt{2}\cdot \pi \cdot d^2\cdot ⟨v⟩\cdot n$ Wstawiając tę wartość do wzoru $\lambda =\frac{⟨v⟩}{\nu }$ otrzymujemy wzór na średnią drogę swobodną cząsteczek $\lambda =\frac{1}{\sqrt{2}\cdot \sigma \cdot n}$ Widzimy, że uwzględnienie ruchu cząsteczek zmniejszyło wartość średniej drogi swobodnej. Pamiętając, że ciśnienie proporcjonalne jest do liczby cząsteczek w jednostce objętości widzimy też, że wraz ze wzrostem ciśnienia maleje średnia droga swobodna. Wzrost temperatury powoduje natomiast wzrost średniej drogi swobodnej, co wiąże się ze zmniejszeniem efektywnej średnicy cząsteczek.

---

Dotychczas zajmowaliśmy się głównie stanami równowagowymi, bądź procesami kwazistatycznymi, które stanowiły faktycznie przechodzenie układu przez ciąg stanów równowagowych. Procesy takie należą także do klasy procesów odwracalnych. W tej lekcji zajmiemy się procesami, które zachodzą w warunkach braku równowagi w układzie. Procesy zmierzające do przywrócenia równowagi prowadza do wzrostu entropii układu, czyli są procesami nieodwracalnymi. Procesy te mają różny charakter i wiążą się z transportem: masy, ciepła, pędu, ładunków elektrycznych itd. Zaliczamy je do klasy zjawisk transportu. Dla ilościowego opisu zjawisk transportu wygodnie jest wprowadzić pojęcie strumienia, czyli wielkości określającej, jaka wartość danej wielkości fizycznej przenoszona jest przez daną powierzchnię w jednostce czasu. Zarówno przenoszone wielkości, jak i powierzchnie mogą być różne; może to być na przykład strumień cieczy bądź strumień światła, może to być przekrój rury, ale może być też powierzchnia zamknięta, jak bańka żarówki itp. Strumień odniesiony do jednostkowej powierzchni prostopadłej do kierunku przepływu nazywać będziemy gęstością strumienia (lub natężeniem strumienia). Występujące w układzie niejednorodności będące przyczyną zjawisk transportu charakteryzowane są przez pochodne funkcji określających przestrzenny rozkład danej wielkości. Rozkład ten odpowiada istnieniu pola danej wielkości fizycznej, np. temperatury lub gęstości. Pochodna wyrażająca szybkość zmian danej wielkości w określonym punkcie pola i w określonym kierunku jest długością wektora zwanego gradientem tej wielkości. Chociaż pojęcie gradientu wprowadzimy formalnie w dalszej części kursu Fizyki, to jednak już teraz będziemy używać go do opisu zjawisk transportu. Dyfuzja - to proces proces zmierzający do wyrównania się koncentracji składników w substancji, stanowiącej niejednorodną mieszaninę, prowadzący w konsekwencji do transportu (przenoszenia) masy. Dyfuzja jest następstwem ruchów cieplnych i zachodzi samorzutnie w ciałach stałych, cieczach i gazach bez oddziaływań zewnętrznych. Weźmy pod uwagę dwuskładnikową mieszaninę. Koncentrację składników niech określa liczba cząsteczek danego rodzaju w jednostce objętości, $n_1$ i $n_2$ , przy czym $n_1+n_2=n$ , gdzie $n$ jest całkowitą liczbą cząsteczek w jednostce objętości. Względną koncentrację cząsteczek danego rodzaju określimy jako $c_i=n_i/n$ . Koncentracja ta nie jest jednak stała w całej objętości. Przyjmijmy, że zmiany koncentracji zachodzą wzdłuż osi $z$ i charakteryzowane są przez wielkości $d{c}_1/dz$ oraz $d{c}_2/dz$ , przy czym $d{c}_1/dz=-d{c}_2/dz$ . Wyrażenie określające strumień cząsteczek danego rodzaju przez powierzchnię prostopadłą do osi $z$ może być zapisane w postaci $N_i=-D\cdot \frac{d{n}_i}{dz}\cdot S$ gdzie $D$ zwane jest współczynnikiem dyfuzji. Występujący tu znak minus jest konsekwencją faktu, że jeśli $d{n}_i/dz>0$ , czyli koncentracja składnika $i$ zwiększa się w kierunku większych wartości $z$ , to strumień związany z dyfuzją ma kierunek przeciwny zmierzając do wyrównania się koncentracji składników. Zwróćmy uwagę, że "siłą motoryczną" zjawiska dyfuzji jest zależność koncentracji od współrzędnej $z$ : $n_i=n_i(z)$. Jeśli $d{n}_i/dz=0$, to znika dyfuzja, $N_i=0$. Wielkość $d{n}_i/dz$ nazywamy gradientem koncentracji w kierunku osi $Z$. Mnożąc obustronnie wyrażenie na strumień cząsteczek danego rodzaju przez masę cząsteczki $m_i$ otrzymujemy wyrażenie określające strumień masy składnika $i$, $M_i=-D\cdot \frac{d{\rho }_i}{dz}\cdot S$ gdzie ${\rho }_i=n_i\cdot m_i$ jest gęstością składnika $i$ w mieszaninie w punkcie, w którym koncentracja tego składnika wynosi $n_i(z)$. Zależność stanowi empiryczne równanie dyfuzji. Sformułowana została w 1855 roku przez niemieckiego fizjologa A. Ficka i nosi nazwę prawa Ficka. Prawo to można wyrazić następująco. Prawo Ficka Strumień substancji dyfundującej przez daną powierzchnię (ustawioną prostopadle do kierunku dyfuzji) jest wprost proporcjonalny do pola tej powierzchni i do szybkości zmiany koncentracji cząsteczek w kierunku dyfuzji. Różnym od dyfuzji procesem transportu masy jest konwekcja, czyli unoszenie. Konwekcja może być spowodowana działaniem sił zewnętrznych (konwekcja wymuszona) lub może zachodzić na skutek różnicy ciśnień spowodowanych różnicami temperatury (konwekcja swobodna). Wtedy z konwekcyjnym transportem masy wiąże się transport ciepła. Konwekcja swobodna ma wielki wpływ na zjawiska atmosferyczne: tworzenie się chmur i prądów powietrznych, prądów morskich itp.

---

W podobny sposób jak to zostało przedstawione dla transportu masy możemy rozważać zagadnienie przewodnictwa cieplnego. Jeśli w ośrodku występują różnice temperatur wzdłuż (umownego) kierunku $Z$ , to pojawia się strumień ciepła określony wzorem $Q_z=-\chi \cdot \frac{dT}{dz}\cdot S$ Strumień ciepła jest proporcjonalny do szybkości zmian temperatury wzdłuż osi $Z$ i do powierzchni $S$ . Wielkość $\chi$ zwana jest współczynnikiem przewodnictwa cieplnego lub przewodnością cieplną ośrodka. Znak minus ma taki sam sens jak w poprzednio. Zależność ta, którą sformułował w 1822 roku francuski fizyk i matematyk Jean Baptiste Joseph Fourier, nosi nazwę prawa Fouriera. Prawo to można wyrazić następująco. Prawo Fouriera Strumień ciepła przez daną powierzchnię jest wprost proporcjonalny do pola tej powierzchni i do szybkości zmiany temperatury w kierunku do powierzchni tej prostopadłym. Przez analogię do zjawiska dyfuzji warto podkreślić, że czynnikiem "motorycznym" przewodnictwa cieplnego, polegającego na transporcie energii kinetycznej chaotycznych ruchów cząsteczek, jest istnienie różnicy temperatury. Zjawisko to, czyli przenoszenie ciepła, zanika, jeśli temperatura w każdym punkcie ośrodka jest jednakowa. Wielkość $dT/dz$ nazywamy gradientem temperatury w kierunku osi $Z$.

---

Kolejnym przykładem zjawiska transportu jest przekaz pędu pomiędzy cząsteczkami ośrodka prowadzący do zjawiska tarcia wewnętrznego. Siłę tarcia poznaliśmy np. na lekcjach z mechaniki cieczy. Siła ta okazała się być proporcjonalna do szybkości zmian prędkości warstw cieczy w jej ruchu laminarnym (warstwowym). Pamiętając, że drugie prawo dynamiki wyraża związek pomiędzy siłą a pędem przekazanym w jednostce czasu $F=dp/dt$ możemy zamienić siłę tarcia wewnętrznego pędem $P$ , przekazywanym w jednostce czasu pomiędzy trącymi się warstwami płynącej cieczy. Uzyskujemy wtedy wyrażenie $P=-\eta \cdot \frac{du}{dz}\cdot S$ gdzie $du/dz$ wyraża szybkość zmian prędkości (gradient) warstw cieczy, a $S$ jest powierzchnią warstw tworzących strumień w kierunku prostopadłym do kierunku osi $Z$. Współczynnik proporcjonalności $\eta$ jest współczynnikiem lepkości. Znak minus po prawej stronie wzoru oznacza, że pęd przekazywany jest w kierunku malenia prędkości. Zauważmy, że wyrażenie to jest podobne do wyrażeń dla rozważanych wcześniej zjawisk: dyfuzji i przewodnictwa cieplnego. W przypadku tarcia wewnętrznego pęd przekazywany między warstwami strumienia cząstek, o kierunku zgodnym z kierunkiem ruchu warstw, jest zależny od tego jak szybko zmienia się prędkość warstw w kierunku $Z$ - prostopadłym do kierunku prędkości warstw $u$. Ta zmiana prędkości jest czynnikiem "motorycznym" przekazywania pędu prowadzącym do wystąpienia zjawiska lepkości. Wielkość $du/dz$ nazywamy gradientem prędkości warstw cieczy w kierunku $Z$.

---

Zadanie 9.1

W zamkniętym zbiorniku jest $m=1g$ argonu. Oblicz zmianę średniej energii kinetycznej atomów po dostarczeniu ciepła $Q=4185J$

Odpowiedź

$⟨\mathrm{\Delta }E⟩\approx 2,77\cdot 10^{-21}J$

---

Zadanie 9.2

Oblicz ciepło właściwe przy stałej objętości dla atomów argonu i cząsteczek azotu

Odpowiedź

Dla argonu $C_V=311Jk{g}^{-1}{K}^{-1}$ , dla azotu $C_V=742Jk{g}^{-1}{K}^{-1}$.

---

Zadanie 9.3

Masa $m=1kg$ azotu pod ciśnieniem $p=10^{5}N/m^2$ ma gęstość $\rho =4kg/m^3$. Średnica każdej z cząsteczek wynosi $d=3,1\cdot 10^{-10}m$. Oblicz, jaką średnią drogę swobodną pokonują cząsteczki.

Odpowiedź

$\lambda =2,7\cdot 10^{-8}m$ .

---

Zadanie 9.4

Oblicz, jaka część cząsteczek gazu ma prędkości różniące się od prędkości najbardziej prawdopodobnej nie więcej niż o $1\mathrm{\%}$

Odpowiedź

$2\mathrm{\Delta }N/N=0,0166$

---

Zadanie 9.5

Podgrzewamy jeden koniec stalowego pręta o długości $L=20cm$ i przekroju poprzecznym $S=3c{m}^2$ do temperatury $T_2=573K$, a drugi jego koniec umieszczamy w naczyniu z mieszaniną wody z lodem (o temperaturze $T_1=273K$). Oblicz masę lodu stopionego w czasie $t=10minut$, zakładając że ciepło rozchodzi się wzdłuż pręta bez strat. Znane są też: współczynnik przewodnictwa cieplnego dla stali $c=0,66J/Ksekcm$ oraz ciepło właściwe topnienia lodu $C=330J/g$.

Odpowiedź

Stopią się 54 g lodu.

---

Słowniczek

statystyczna interpretacja temperatury	temperatura jest miarą średniej energii kinetycznej chaotycznego ruchu cząsteczek.
liczba stopni swobody	(dla układu mechanicznego) liczba niezależnych wielkości za pomocą, których może być opisane położenie układu.
zasada ekwipartycji energii	na każdy stopień swobody cząsteczki przypada średnio ta sama energia równa $kT/2$.
strumień	wielkość określająca jaka wartość danej wielkości fizycznej przenoszona jest przez określoną powierzchnię (często przyjmuje się powierzchnię jednostkową) w jednostce czasu.
koncentracja	liczba cząsteczek danego rodzaju w jednostce objętości
gęstość strumienia	strumień odniesiony do jednostkowej powierzchni prostopadłej do kierunku przepływu.
gradient pola	wektor wyrażający szybkość zmian w przestrzeni danej wielkości charakteryzującej pole w określonym punkcie pola i w określonym kierunku.
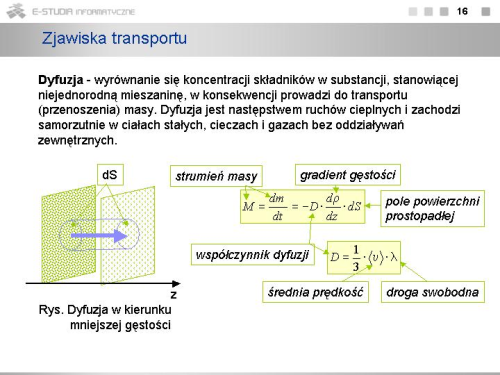
dyfuzja	proces przenoszenia masy zmierzający do wyrównania się koncentracji składników w substancji, stanowiącej niejednorodną mieszaninę. Dyfuzja jest następstwem ruchów cieplnych i zachodzi samorzutnie w ciałach stałych, cieczach i gazach.
prawo Ficka	Strumień substancji dyfundującej przez daną powierzchnię (ustawioną prostopadle do kierunku dyfuzji) jest proporcjonalny do pola tej powierzchni i szybkości zmiany (gradientu) koncentracji cząsteczek w kierunku prostopadłym do powierzchni.
konwekcja	proces w którym masa lub/i ciepło przenoszone są poprzez przemieszczające się masy gazu lub cieczy pod wpływem czynników zewnętrznych.
przewodnictwo cieplne	zjawisko przenoszenia w ośrodku energii kinetycznej chaotycznych ruchów cieplnych cząsteczek, pojawiające się w ośrodku, kiedy występują różnice temperatur.
tarcie wewnętrzne (lepkość)	przekaz pędu pomiędzy przemieszczającymi się względem siebie warstwami ośrodka.
prawo Fouriera	Strumień ciepła przez daną powierzchnię jest wprost proporcjonalny do pola tej powierzchni i do szybkości zmiany temperatury cząsteczek w kierunku prostopadłym do tej powierzchni.
efektywna średnica cząsteczki	odległość między środkami cząsteczek przy ich największym zbliżeniu.
przekrój czynny na zderzenie	efektywne pole powierzchni, jakie cząsteczka stanowi w procesie wzajemnych zderzeń.
średnia droga swobodna	średnia droga pomiędzy zderzeniami w chaotycznym ruchu cząsteczek.

---