PEE Moduł 14: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 11: | Linia 11: | ||
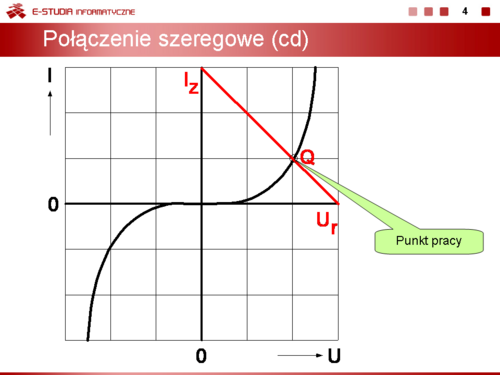
Mając do dyspozycji charakterystyki elementu nieliniowego można wykonać graficzną analizę obwodu zawierającego ten element. Przy połączeniu szeregowym przedstawionym na slajdzie suma napięć na elementach jest stała i równa się <math>E\,</math>. | Mając do dyspozycji charakterystyki elementu nieliniowego można wykonać graficzną analizę obwodu zawierającego ten element. Przy połączeniu szeregowym przedstawionym na slajdzie suma napięć na elementach jest stała i równa się <math>E\,</math>. | ||
<math>E=I_QR+U_Q</math> | <math>E=I_QR+U_Q</math> | ||
| Linia 32: | Linia 31: | ||
<math>\displaystyle I_z=\frac{E}{R},\, U_z = 0 V</math> przy zwarciu, | <math>\displaystyle I_z=\frac{E}{R},\, U_z = 0 V</math> przy zwarciu, | ||
<math>\displaystyle I_r = 0\, A,\, U_r = E</math> przy rozwarciu. | <math>\displaystyle I_r = 0\, A,\, U_r = E</math> przy rozwarciu. | ||
Punkt przecięcia prostej z charakterystyką elementu nieliniowego wyznacza punkt pracy Q tego elementu oraz obwodu liniowego. Często prostą, która jest obrazem charakterystyki części liniowej obwodu nazywamy prostą obciążenia elementu nieliniowego (np. diody lub tranzystora). | Punkt przecięcia prostej z charakterystyką elementu nieliniowego wyznacza punkt pracy Q tego elementu oraz obwodu liniowego. Często prostą, która jest obrazem charakterystyki części liniowej obwodu nazywamy prostą obciążenia elementu nieliniowego (np. diody lub tranzystora). | ||
| Linia 55: | Linia 54: | ||
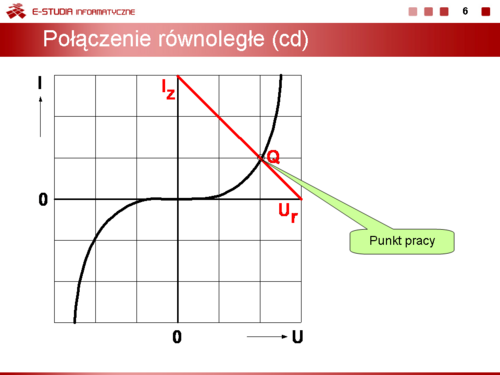
|valign="top"|Konstrukcją graficzna umożliwiająca wyznaczeniu punktu pracy elementu nieliniowego jest identyczna jak w przypadku połączenia szeregowego. Zwierając | |valign="top"|Konstrukcją graficzna umożliwiająca wyznaczeniu punktu pracy elementu nieliniowego jest identyczna jak w przypadku połączenia szeregowego. Zwierając | ||
i rozwierając zaciski A i B obwodu otrzymujemy współrzędne prostej obciążenia | i rozwierając zaciski A i B obwodu otrzymujemy współrzędne prostej obciążenia | ||
<math>\displaystyle I_z = I,\, U_z = 0\, V</math> przy zwarciu, | <math>\displaystyle I_z = I,\, U_z = 0\, V</math> przy zwarciu, | ||
| Linia 140: | Linia 138: | ||
<math>U_r = U_C_E_r = E_C</math> | <math>U_r = U_C_E_r = E_C</math> | ||
Punkt przecięcia tak wyznaczonej prostej (prostej obciążenia) z charakterystyką tranzystora odpowiadającą prądowi <math>I_B</math> który w tym wypadku będzie również stanowił prąd IBQ wyznaczy współrzędne punktu pracy <math>I_C_Q</math> oraz <math>U_C_E_Q</math> tranzystora. | Punkt przecięcia tak wyznaczonej prostej (prostej obciążenia) z charakterystyką tranzystora odpowiadającą prądowi <math>I_B</math> który w tym wypadku będzie również stanowił prąd IBQ wyznaczy współrzędne punktu pracy <math>I_C_Q</math> oraz <math>U_C_E_Q</math> tranzystora. | ||
| Linia 150: | Linia 147: | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd16.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd16.png|thumb|500px]] | ||
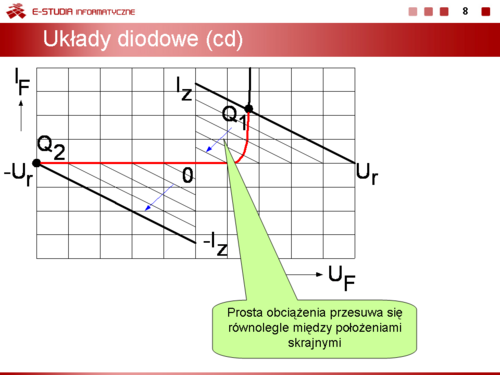
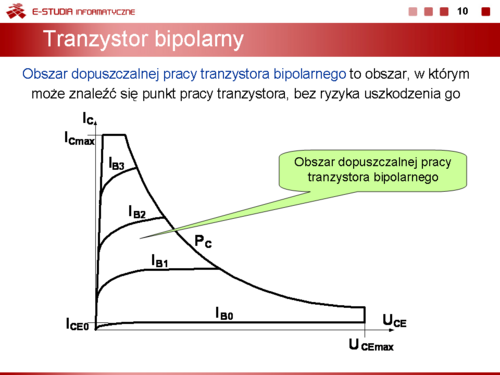
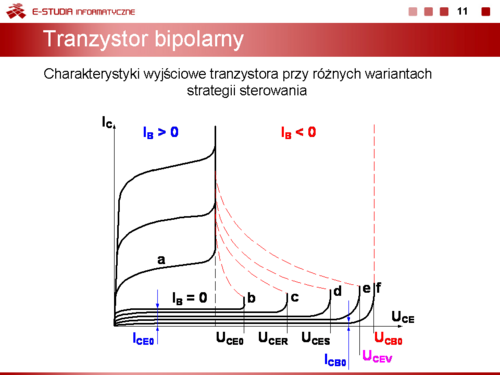
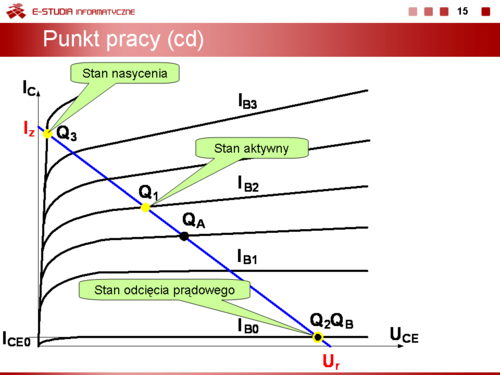
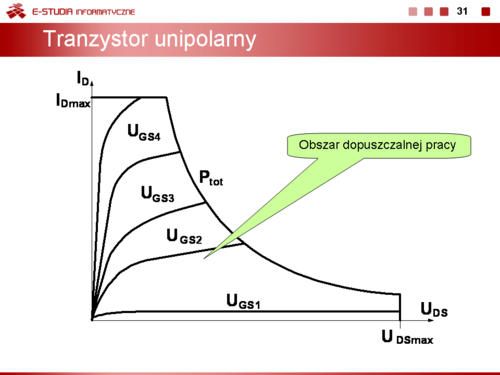
|valign="top"|W zależności od położenia punktu pracy w polu charakterystyk tranzystora wyróżnia się: | |valign="top"|W zależności od położenia punktu pracy w polu charakterystyk tranzystora wyróżnia się: | ||
*stan przewodzenia aktywnego, kiedy punkt pracy leży wewnątrz obszaru dopuszczalnej pracy (np. punkt <math>Q_1</math> na slajdzie 15). W tym stanie prąd kolektora i napięcie kolektor-emiter mają stosunkowo duże wartości. | *stan przewodzenia aktywnego, kiedy punkt pracy leży wewnątrz obszaru dopuszczalnej pracy (np. punkt <math>Q_1\,</math> na slajdzie 15). W tym stanie prąd kolektora i napięcie kolektor-emiter mają stosunkowo duże wartości. | ||
*stan odcięcia prądowego, kiedy punkt pracy znajduje się na najniżej położonej charakterystyce (np. punkt | *stan odcięcia prądowego, kiedy punkt pracy znajduje się na najniżej położonej charakterystyce (np. punkt <math>Q_2\,</math> na slajdzie15). W tym stanie tranzystor praktycznie nie przewodzi, prąd kolektora jest pomijalnie mały (np. równy <math>I_C_E_0</math>), a napięcie kolektor-emiter jest porównywalne lub równe napięciu zasilania. | ||
*stan nasycenia prądowego, kiedy punkt pracy leży w obszarze nasycenia (na tzw. prostej nasycenia, np. punkt <math>Q_3</math> na slajdzie 15). W tym stanie tranzystor zachowuje się jak zamknięty łącznik, prąd kolektora jest duży, a napięcie kolektor-emiter jest praktycznie równe 0 V (pomijamy w tym wypadku napięcie nasycenia tranzystora <math>U_C_E_s | *stan nasycenia prądowego, kiedy punkt pracy leży w obszarze nasycenia (na tzw. prostej nasycenia, np. punkt <math>Q_3\,</math> na slajdzie 15). W tym stanie tranzystor zachowuje się jak zamknięty łącznik, prąd kolektora jest duży, a napięcie kolektor-emiter jest praktycznie równe 0 V (pomijamy w tym wypadku napięcie nasycenia tranzystora <math>U_C_E_s\approx 0,2\, V</math>). | ||
|} | |} | ||
| Linia 172: | Linia 169: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd18.png|thumb|500px]] | ||
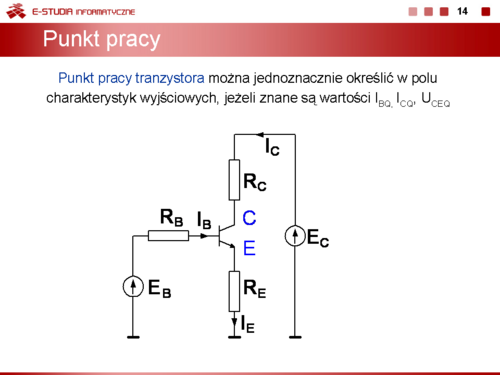
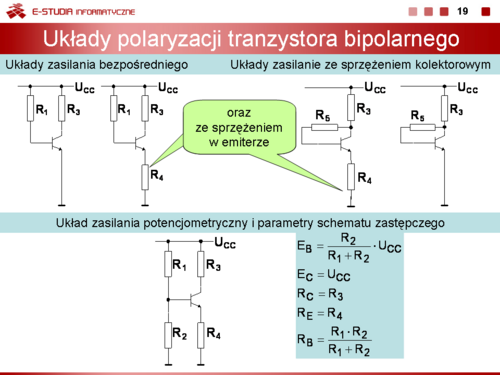
|valign="top"|Współrzędne punktu pracy tranzystora bipolarnego <math>I_C_Q i u_C_E_Q</math> zależą od parametrów obwodu zewnętrznego dołączonego do tranzystora (napięcie zasilania <math>U_C_C</math>, rezystory <math>R_C, R_E, R_B</math>) oraz od parametrów tranzystora. Przyjmuje się, z pośród wielu parametrów tranzystora trzy z nich: napięcie <math>U_B_E</math>, prąd <math>I_{CB0}</math>, współczynnik wzmocnienia prądowego <math>\ | |valign="top"|''Współrzędne punktu pracy tranzystora bipolarnego'' <math>I_C_Q\</math> i <math>u_C_E_Q</math> zależą od parametrów obwodu zewnętrznego dołączonego do tranzystora (napięcie zasilania <math>U_C_C</math>, rezystory <math>R_C,\, R_E,\, R_B\,</math>) oraz od parametrów tranzystora. Przyjmuje się, z pośród wielu parametrów tranzystora trzy z nich: napięcie <math>U_B_E\,</math>, prąd <math>I_{CB0}\,</math>, współczynnik wzmocnienia prądowego <math>\alpha_0</math> lub <math>\beta_0</math> , są potrzebna do jednoznacznego określenia punktu pracy tranzystora. | ||
Obwód przedstawiony na slajdzie 18 można opisać układem równań | Obwód przedstawiony na slajdzie 18 można opisać układem równań | ||
<math>E_B=I_{BQ}R_B+I_{EQ}R_E+U_{BEQ}</math> | <math>\displaystyle E_B=I_{BQ}\cdot R_B+I_{EQ}\cdot R_E+U_{BEQ}</math> | ||
<math>E_C=I_{CQ}R_C+I_{EQ}R_E+U_{CEQ}</math> | <math>\displaystyle E_C=I_{CQ}\cdot R_C+I_{EQ}\cdot R_E+U_{CEQ}</math> | ||
<math>I_{EQ}=I_{CQ}I_{BQ}</math> | <math>\displaystyle I_{EQ}=I_{CQ}+I_{BQ}</math> | ||
<math>I_{CQ}=\beta_{0Q}I_{BQ}+(1+\beta _{0Q})I_{CB0Q}</math> | <math>\displaystyle I_{CQ}=\beta_{0Q}\cdot I_{BQ}+(1+\beta _{0Q})\cdot I_{CB0Q}</math> | ||
Przekształcając ten układ obliczamy współrzędne punktu pracy | Przekształcając ten układ obliczamy współrzędne punktu pracy | ||
<math>I_{CQ}=\frac{\ | <math>\displaystyle I_{CQ}=\frac{\displaystyle \beta_{0Q}(E_B-U_{BEQ})+(\beta_{0Q}+1)I_{CB0Q}(R_B+R_E)}{\displaystyle R_B+(1+\beta_{0Q})R_E}</math> | ||
<math>U_{CEQ}=E_C-I_{CQ}[R_C+\frac{(\beta_{0Q}+1)R_E}{\beta_{0Q}}]+\frac{\beta _{0Q}+1}{\beta_{0Q}}I_{CB0Q}R_E</math> | <math>\displaystyle U_{CEQ}=E_C-I_{CQ}\bigg[R_C+\frac{\displaystyle (\beta_{0Q}+1)R_E}{\displaystyle \beta_{0Q}}\bigg]+\frac{\beta _{0Q}+1}{\beta_{0Q}}I_{CB0Q}R_E</math> | ||
|} | |} | ||
Wersja z 19:53, 13 wrz 2006
 |
Wykład 14. Podstawowe topologie połączeń elementów półprzewodnikowych: punkt pracy, stany pracy
|
 |
Przy połączeniu równoległym suma prądów jest stała i równa I.
Podobnie jak przy połączeniu szeregowym prąd IQ oraz napięcie UQ określają współrzędne punktu pracy elementu nieliniowego. |
 |
Warianty sterowania |
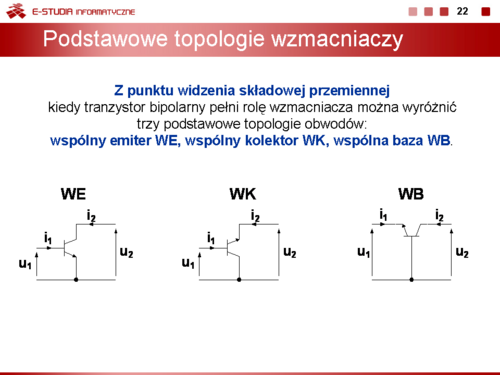 |
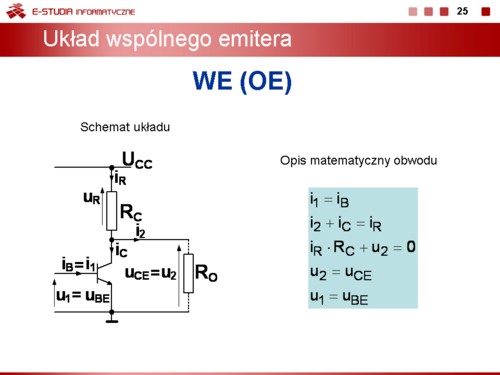
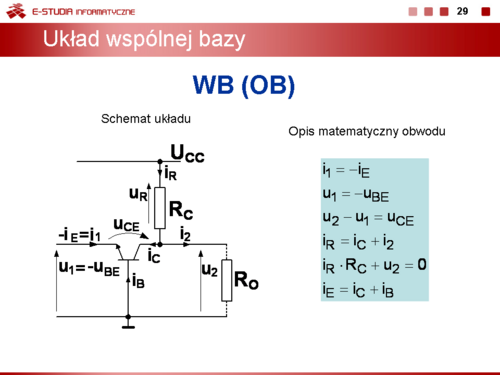
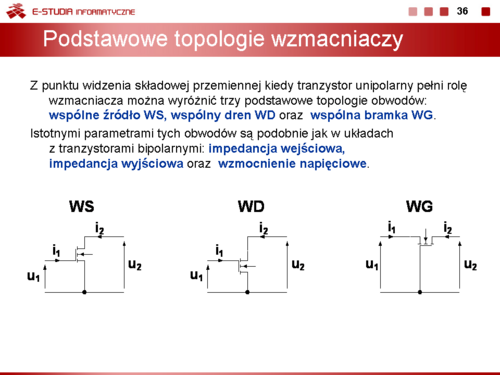
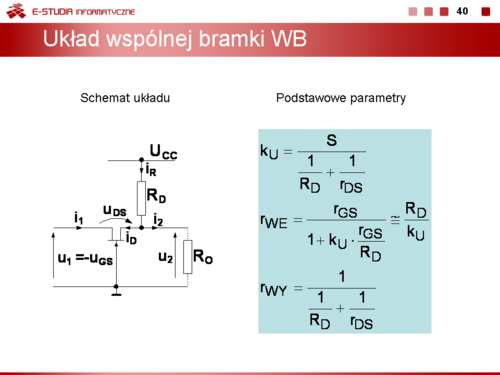
Z punktu widzenia składowej przemiennej kiedy tranzystor bipolarny pełni rolę wzmacniacza można wyróżnić trzy podstawowe topologie obwodów: wspólny emiter WE, wspólny kolektor WK, wspólna baza WB. |
 |
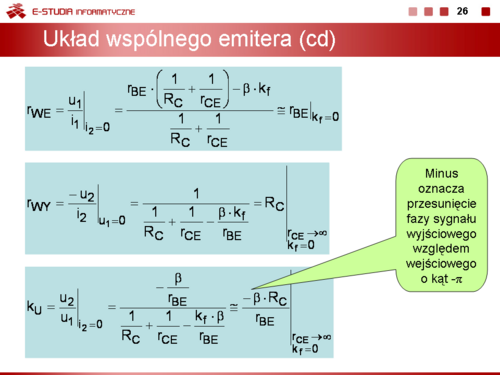
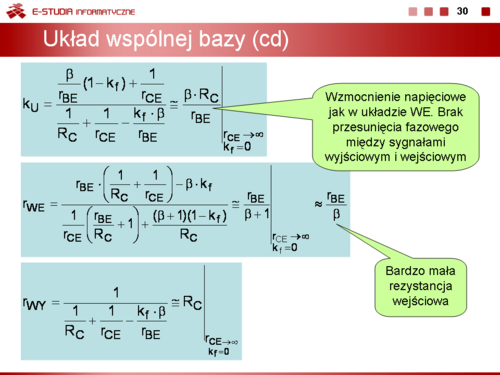
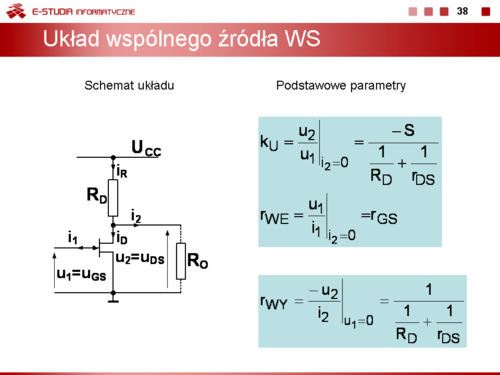
Istotnymi parametrami tych obwodów są
Znak minus w definicji rezystancji wyjściowej wynika z przyjęcia, przeciwnego niż to jest przyjęte w teorii czwórników, zwrotu prądu |
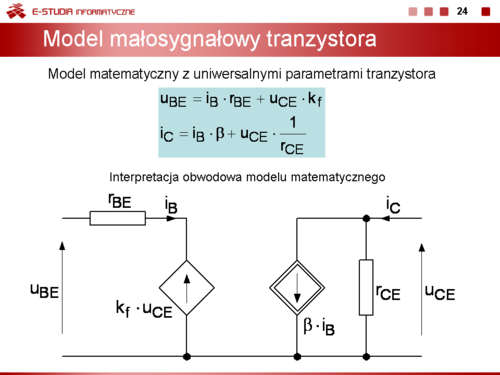 |
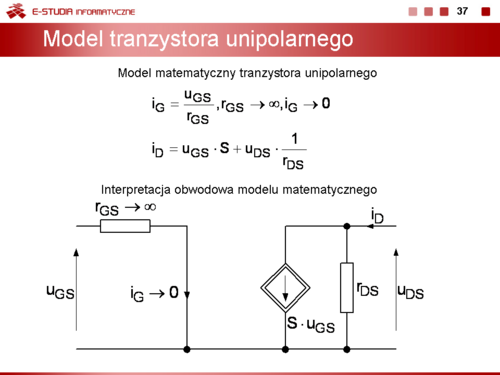
Przy wyznaczaniu tych parametrów stosuje się małosygnałowy model tranzystora bipolarnego opisany równaniami macierzy hybrydowej h z parametrami w postaci uniwersalnej.
|
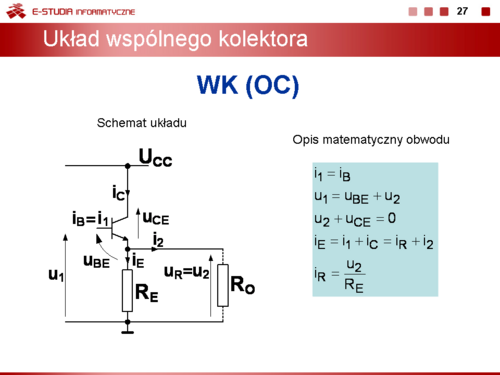 |
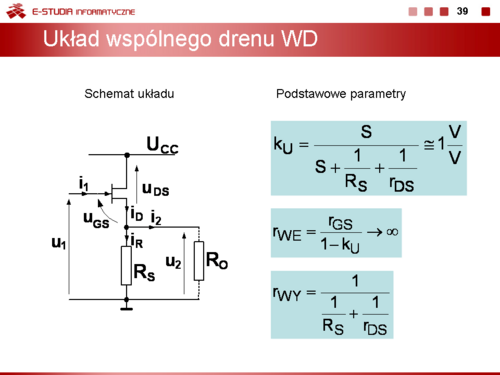
Dla układu wspólnego kolektora WK, często nazywanego także wtórnikiem emiterowym można zapisać
|
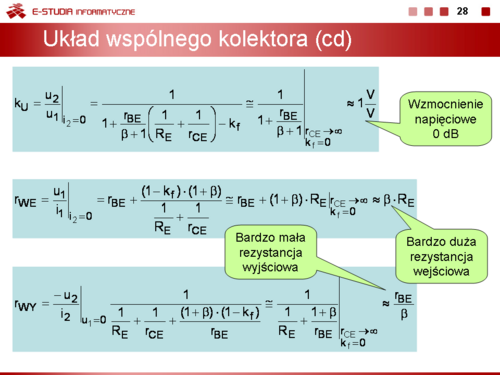 |
Wzmocnienie napięciowe tego układu jest bliskie, ale zawsze mniejsze od jedności
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|