PEE Moduł 14: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 182: | Linia 182: | ||
<math>I_{CQ}=\beta_{0Q}I_{BQ}+(1+\beta _{0Q})I_{CB0Q}</math> | <math>I_{CQ}=\beta_{0Q}I_{BQ}+(1+\beta _{0Q})I_{CB0Q}</math> | ||
Przekształcając ten układ obliczamy współrzędne punktu pracy | |||
<math>I_{CQ}=\frac{\BETA_{0Q}(E_B-U_{BEQ})+(\beta_{0Q}+1)I_{CB0Q}(R_B+R_E)}{R_B+(1+\beta_{0Q})R_E}</math> | |||
<math>U_{CEQ}=E_C-I_{CQ}[R_C+\frac{(\beta_{0Q}+1)R_E}{\beta_{0Q}}]+\frac{\beta _{0Q}+1}{\beta_{0Q}}I_{CB0Q}R_E</math> | |||
|} | |} | ||
| Linia 192: | Linia 192: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd19.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd19.png|thumb|500px]] | ||
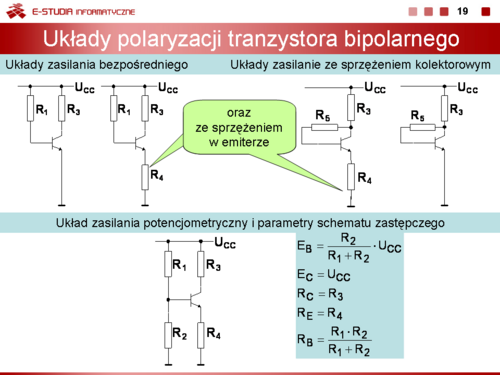
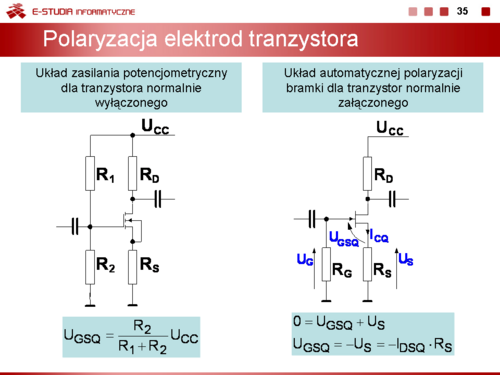
|valign="top"| | |valign="top"|Istnieje wiele układów linowych i nieliniowych umożliwiających polaryzację elektrod | ||
i ustawianie punktu pracy tranzystora bipolarnego. Na slajdzie 19 przedstawiono najbardziej popularne układy liniowe. Każdy z tych obwodów można sprowadzić, stosując twierdzenie Thevenina, do postaci ogólnej przedstawionej na slajdzie 18. | |||
Np. Zastępcze parametry obwodu zasilania dla układu z potencjometrycznym zasilaniem bazy i sprzężeniem w emiterze są odpowiednio równe: | |||
<math>E_B\frac{R_2}{R_1+R_2}U_{CC}</math> | |||
<math>E_C=U_{CC}</math> | |||
<math>R_C=R_3</math> | |||
<math>R_E=R_4</math> | |||
<math>R_B=\frac{R_1 R_2}{R_1+R_2}</math> | |||
|} | |} | ||
| Linia 199: | Linia 211: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M14_Slajd20.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M14_Slajd20.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Istotnym zagadnieniem w przypadku zasilania tranzystorów bipolarnych jest stabilizacja termiczna punktu pracy umożliwiająca zmniejszenie wpływu zmian parametrów tranzystora pod wpływem temperatury, na położenie punktu pracy. | ||
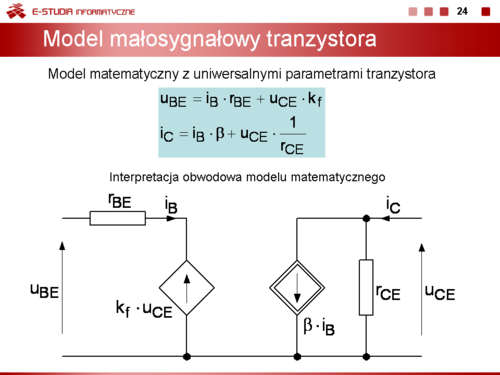
Przyjmując, że zmianie ulegają parametry tranzystora równanie stabilizacji punktu pracy ma następującą postać | |||
<math>dl_{CQ}=\frac{\delta l_{CQ}}{\delta l_{CB0}}dl_{CB0}+\frac{\delta l_{CQ}}{\delta U_{BE}}dU_{BE}+\frac{\delta l_{CQ}}{\delta \beta_0}d\beta_0</math> | |||
|} | |} | ||
Wersja z 13:30, 12 wrz 2006
 |
Wykład 14. Podstawowe topologie połączeń elementów półprzewodnikowych: punkt pracy, stany pracy
|
 |
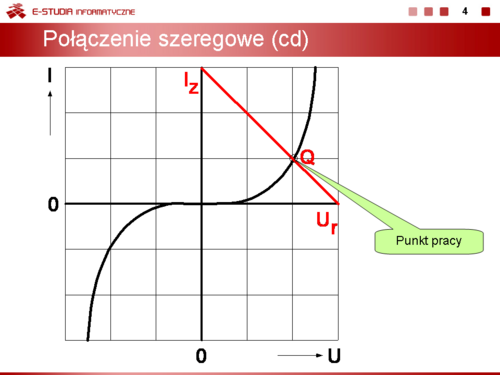
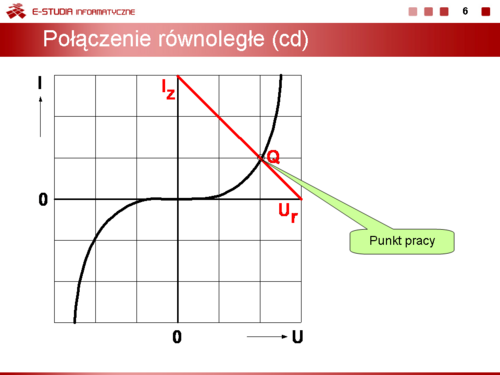
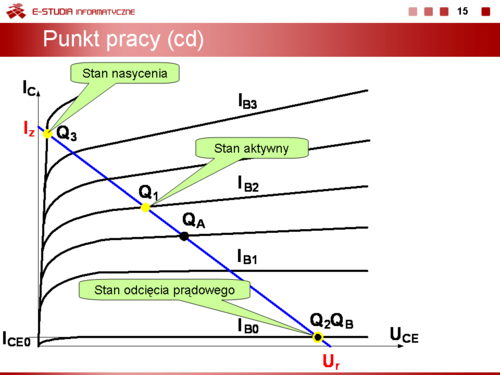
Przy połączeniu równoległym suma prądów jest stała i równa I.
Podobnie jak przy połączeniu szeregowym prąd IQ oraz napięcie UQ określają współrzędne punktu pracy elementu nieliniowego. |
 |
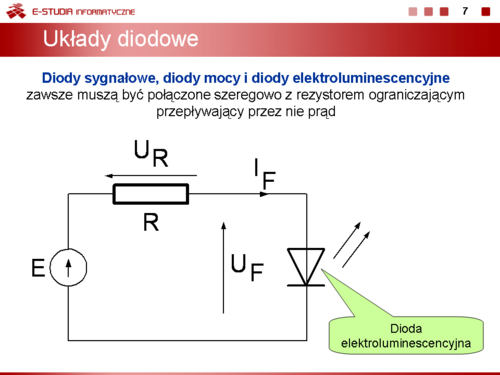
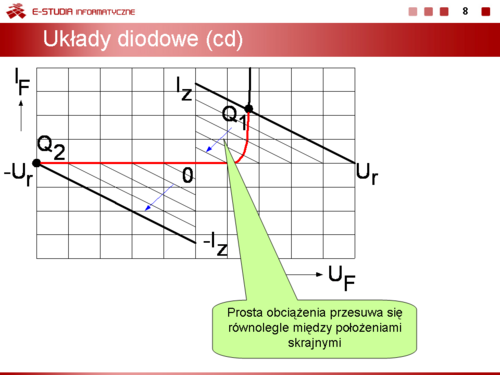
Warianty sterowania |
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
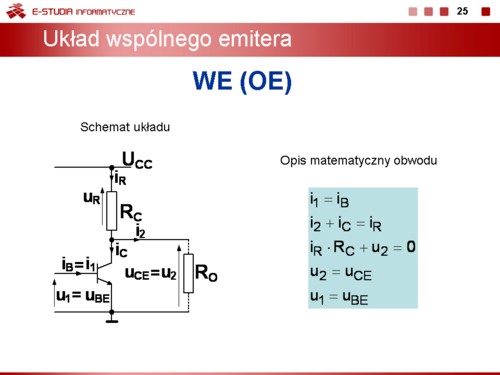 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
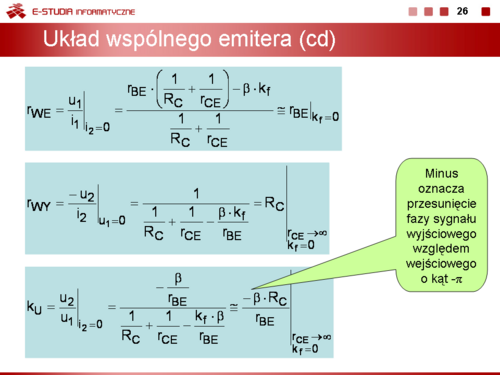 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
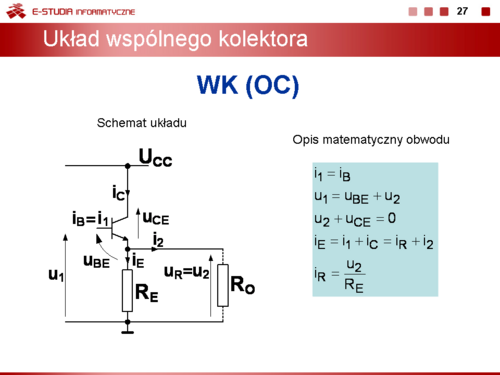 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
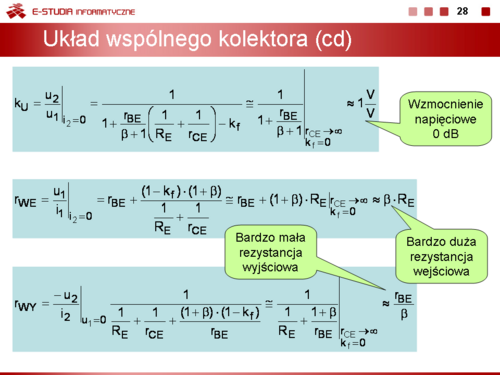 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
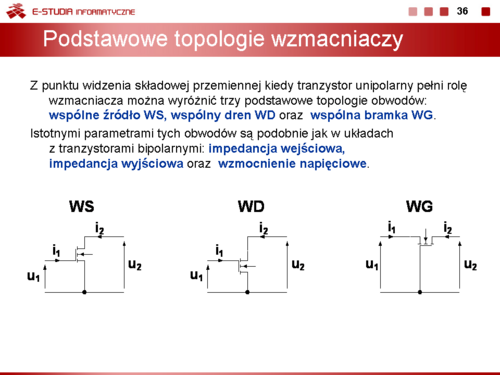 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
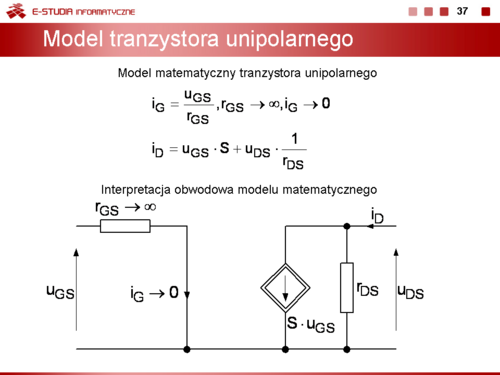 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
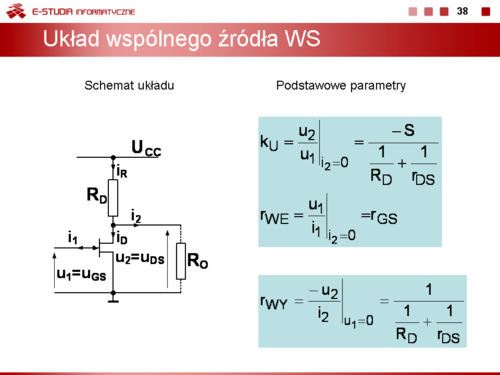 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
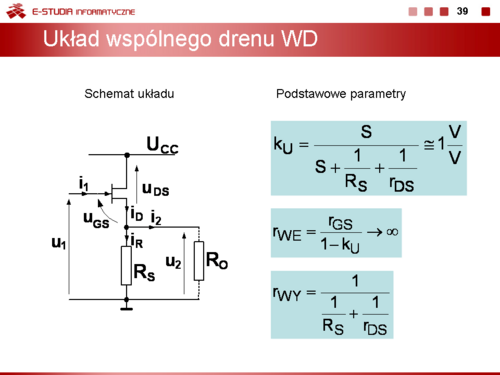 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|
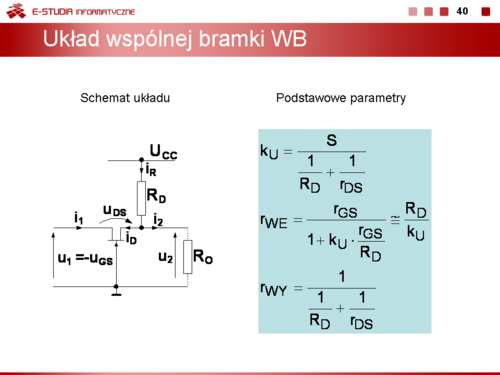 |
Slajd 1. Podstawy fizyczne działania elementów półprzewodnikowych.
|