PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 120: | Linia 120: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd6.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd6.png|500px]] | ||
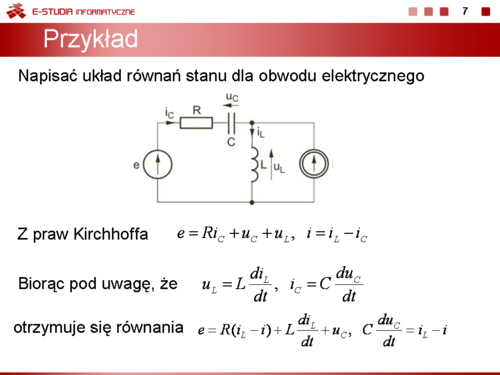
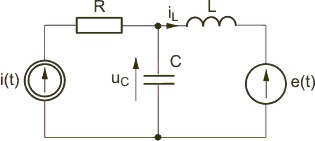
|valign="top"|Kolejny przykład pokazuje jak napisać układ równań stanu dla obwodu elektrycznego. | |valign="top"|Kolejny przykład pokazuje jak napisać układ równań stanu dla obwodu elektrycznego. Z praw Kirchhoffa napisanych dla obwodu z rysunku obok wynikają następujące równania | ||
Z praw Kirchhoffa napisanych dla obwodu z rysunku obok wynikają następujące równania | |||
: <math>e=Ri_C+u_C+u_L</math> | : <math>e=Ri_C+u_C+u_L</math> | ||
: <math>i=i_L=L-i_C</math> | : <math>i=i_L=L-i_C</math> | ||
Biorąc pod uwagę, że | Biorąc pod uwagę, że | ||
: <math>u_L=L\frac{di_L}{dt}</math>, <math>i_C=C\frac{du_C}{dt}</math> | : <math>u_L=L\frac{di_L}{dt}</math>, <math>i_C=C\frac{du_C}{dt}</math> | ||
równania Kirchhoffa można przekształcić do równoważnej postaci równań różniczkowych | równania Kirchhoffa można przekształcić do równoważnej postaci równań różniczkowych | ||
| Linia 140: | Linia 135: | ||
: <math>C\frac{du_C}{dt}=i_L-i</math> | : <math>C\frac{du_C}{dt}=i_L-i</math> | ||
które przyjmują uporządkowaną formę odpowiadającą postaci | które przyjmują uporządkowaną formę odpowiadającą postaci | ||
| Linia 154: | Linia 148: | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd7.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd7.png|500px]] | ||
|valign="top"|Równania powyższe można zapisać w postaci zależności macierzowej równania stanu, w której zmiennymi stanu są prąd cewki i napięcie kondensatora | |valign="top"|Równania powyższe można zapisać w postaci zależności macierzowej równania stanu, w której zmiennymi stanu są prąd cewki i napięcie kondensatora | ||
: <math>\begin{bmatrix}\frac{di_L}{dt}\\ \frac{du_C}{dt}\end{bmatrix}=\begin{bmatrix}\frac{-R}{L}&\frac{-1}{L} \\ \frac{1}{C}& 0\end{bmatrix}\begin{bmatrix}i_L\\u_C\end{bmatrix}+\begin{bmatrix}\frac{1}{L}&\frac{R}{L}\\ 0& \frac{-1}{C}\end{bmatrix}\begin{bmatrix}e\\i\end{bmatrix}</math> | : <math>\begin{bmatrix}\frac{di_L}{dt}\\ \frac{du_C}{dt}\end{bmatrix}=\begin{bmatrix}\frac{-R}{L}&\frac{-1}{L} \\ \frac{1}{C}& 0\end{bmatrix}\begin{bmatrix}i_L\\u_C\end{bmatrix}+\begin{bmatrix}\frac{1}{L}&\frac{R}{L}\\ 0& \frac{-1}{C}\end{bmatrix}\begin{bmatrix}e\\i\end{bmatrix}</math> | ||
Wektor stanu <math>\mathbf{x}</math> oraz wektor wymuszeń <math>\mathbf{u}</math> są równe | Wektor stanu <math>\mathbf{x}</math> oraz wektor wymuszeń <math>\mathbf{u}</math> są równe | ||
: <math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | : <math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | ||
Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu <math>\mathbf{A}</math> jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz <math>\mathbf{B}</math> zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu <math>\mathbf{A}</math> o postaci | Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu <math>\mathbf{A}</math> jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz <math>\mathbf{B}</math> zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu <math>\mathbf{A}</math> o postaci | ||
: <math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | : <math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | ||
Wersja z 09:26, 8 wrz 2006

|

|
Równania obwodu w stanie ustalonym
|
| Zadania sprawdzające
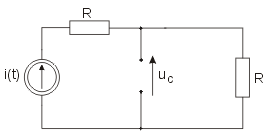
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku
Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
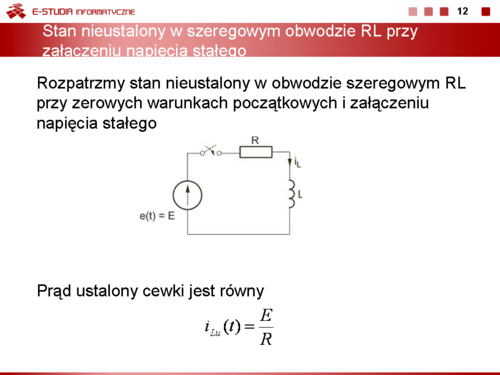
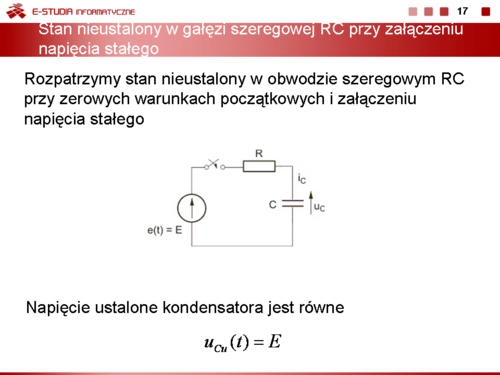
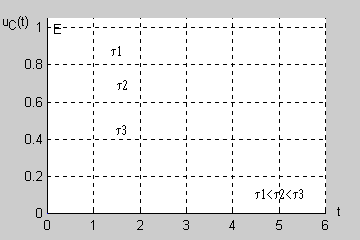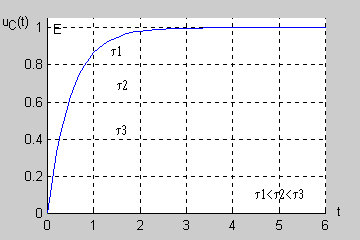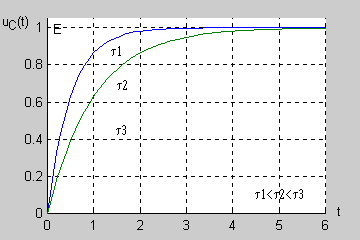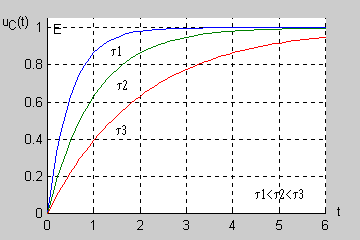
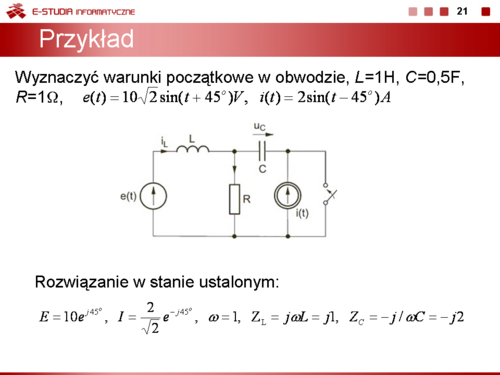
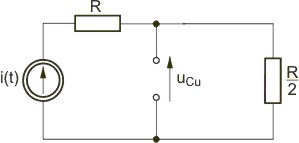
Zadanie 7.2 Określić przebieg czasowy napięcia na kondensatorze w stanie nieustalonym w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów: .
Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
Schemat obwodu w stanie ustalonym po przełączeniu
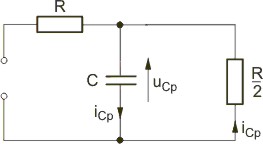
Schemat obwodu w stanie przejściowym po przełączeniu
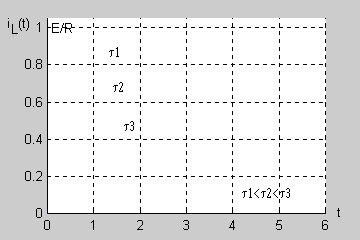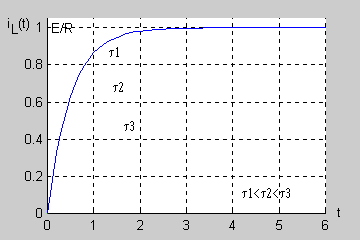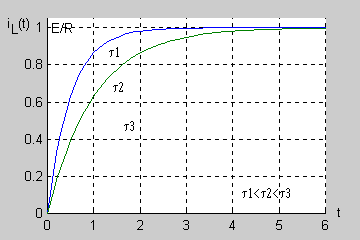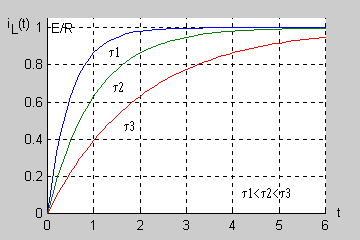
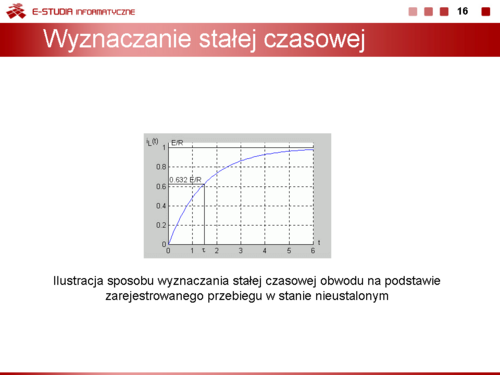
Stała czasowa obwodu jest więc równa . |