PS Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 24: | Linia 24: | ||
|valign="top"| | |valign="top"| | ||
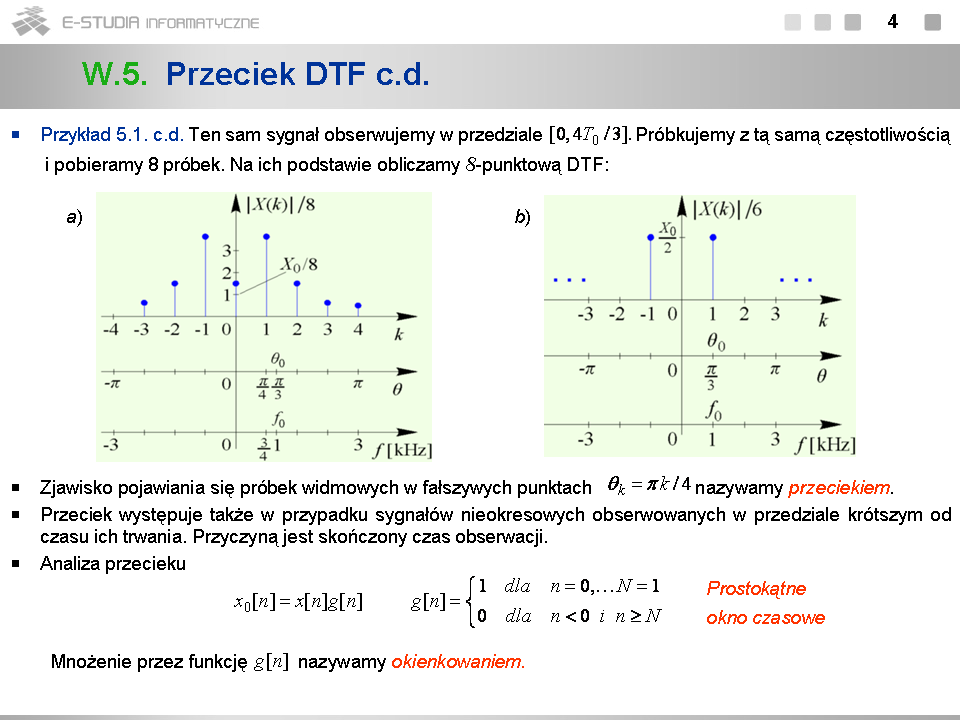
*Zgodnie z właściwością symetrii wystarczy obliczyć tylko próbki widmowe <math>X(0), X(1), X(2), X(3)\,</math> . Jak widzimy tylko próbki <math>X(1)\,</math> i <math>X(5)\,</math> (lub równoważnie <math>X(-1)\,</math> ) są niezerowe. | *Zgodnie z właściwością symetrii wystarczy obliczyć tylko próbki widmowe <math>X(0), X(1), X(2), X(3)\,</math> . Jak widzimy tylko próbki <math>X(1)\,</math> i <math>X(5)\,</math> (lub równoważnie <math>X(-1)\,</math> ) są niezerowe. | ||
*Gdy analogowy sygnał harmoniczny jest obserwowany dokładnie tylko przez jeden jego okres, wówczas DTF wyznaczone na podstawie jego próbek daje prawidłowy obraz jego widma. Niezerowe próbki widmowe otrzymujemy tylko dla pulsacji unormowanych <math>\theta\pm \pi/3\,</math> odpowiadających częstotliwościom nieunormowanym <math>f=\pm 1\, kHz</math> . | *Gdy analogowy sygnał harmoniczny jest obserwowany dokładnie tylko przez jeden jego okres, wówczas DTF wyznaczone na podstawie jego próbek daje prawidłowy obraz jego widma. Niezerowe próbki widmowe otrzymujemy tylko dla pulsacji unormowanych <math>\theta =\pm \pi/3\,</math> odpowiadających częstotliwościom nieunormowanym <math>f=\pm 1\, kHz</math> . | ||
|} | |} | ||
| Linia 34: | Linia 34: | ||
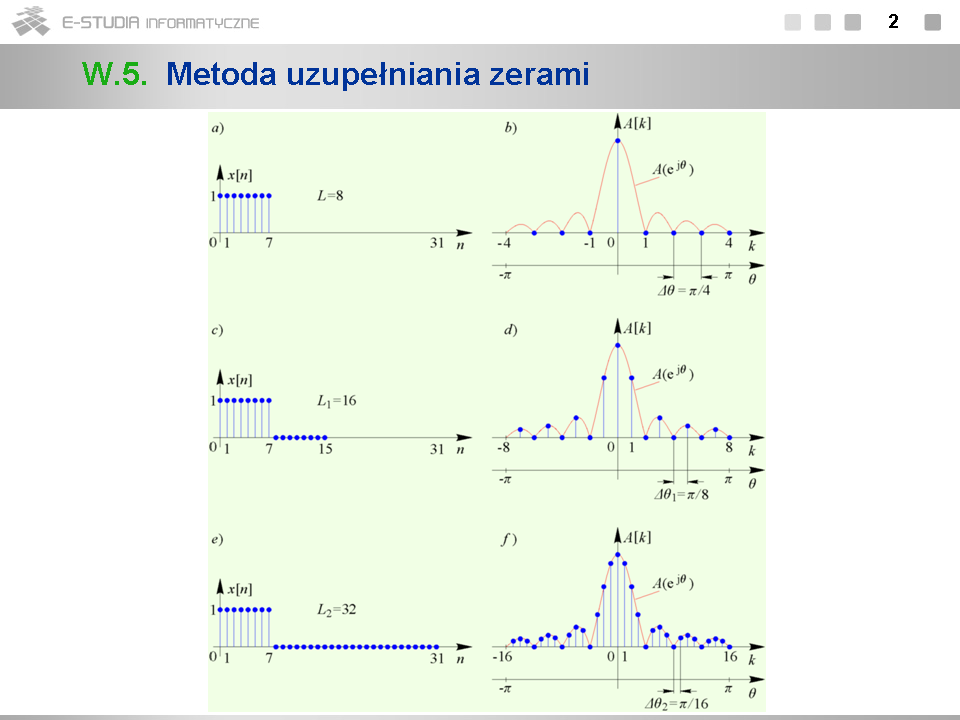
*Punkty <math>\theta_k =\pi k/4</math> odpowiadają częstotliwością nieunormowanym <math>f_k=k\times 0,75\, kHz</math> , nie pokrywającymi się z właściwą częstotliwością sygnału <math>1\, kHz</math> . | *Punkty <math>\theta_k =\pi k/4</math> odpowiadają częstotliwością nieunormowanym <math>f_k=k\times 0,75\, kHz</math> , nie pokrywającymi się z właściwą częstotliwością sygnału <math>1\, kHz</math> . | ||
*Można mówić o przecieku mocy sygnału skoncentrowanej w prążku widmowym o częstotliwości <math>1\, kHz</math> do prążków widmowych występujących w fałszywych punktach osi częstotliwości. | *Można mówić o przecieku mocy sygnału skoncentrowanej w prążku widmowym o częstotliwości <math>1\, kHz</math> do prążków widmowych występujących w fałszywych punktach osi częstotliwości. | ||
*Obserwacja sygnału <math>x[n]\,</math> w skończonym przedziale czasu <math>n= | *Obserwacja sygnału <math>x[n]\,</math> w skończonym przedziale czasu <math>n=0,...,N-1\,</math> odpowiada mnożeniu tego sygnału przez prostokątne okno czasowe. Mówimy wówczas o okienkowaniu sygnału. | ||
|} | |} | ||
| Linia 64: | Linia 64: | ||
|valign="top"| | |valign="top"| | ||
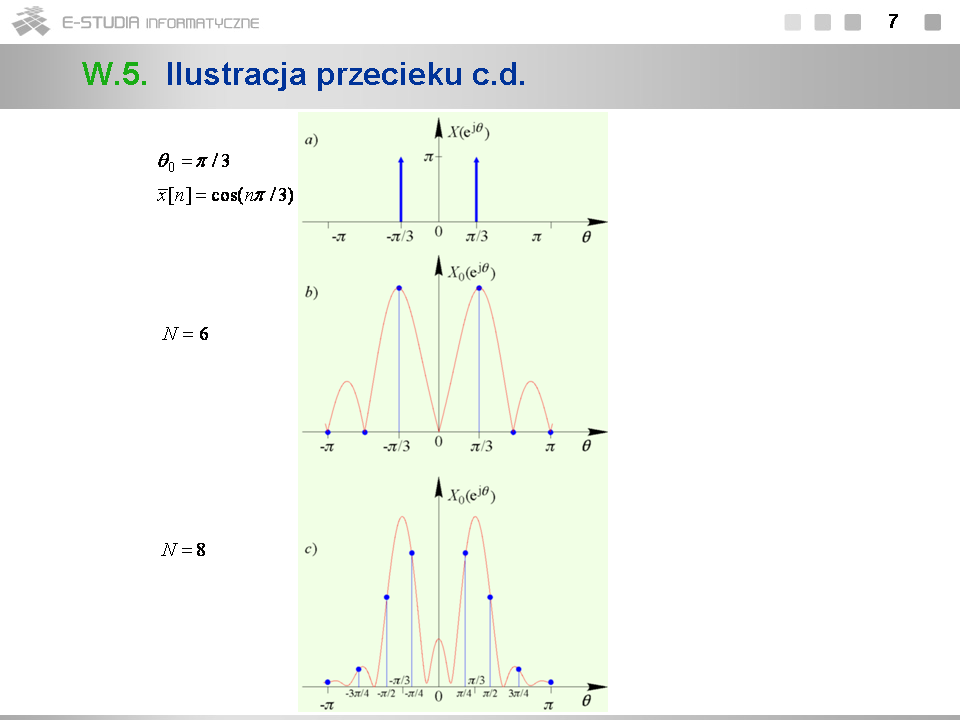
*Na rys. b i c pokazano wykresy widma amplitudowego sygnału harmonicznego z przykładu 5.2 o pulsacji unormowanej <math>\theta_0 =\pi /3</math> okienkowanego oknem prostokątnym w dwóch przypadkach: <math>N=6\,</math> oraz <math>N=8\,</math> . | *Na rys. b i c pokazano wykresy widma amplitudowego sygnału harmonicznego z przykładu 5.2 o pulsacji unormowanej <math>\theta_0 =\pi /3</math> okienkowanego oknem prostokątnym w dwóch przypadkach: <math>N=6\,</math> oraz <math>N=8\,</math> . | ||
*Wykres wyjaśnia dlaczego w przypadku wyznaczenia 6-punktowej DTF (rys. b) nie występuje zjawisko przecieku, tzn. otrzymujemy prawidłowe próbki widma sygnału harmonicznego w punktach <math>\pm \pi/3\,</math> (dla <math>k\pm 1\,</math> ). Pozostałe próbki widmowe, składające się na DFT, wypadają bowiem dokładnie w punktach zerowych rozmytego widma <math>X_0 (e^{j\theta})</math> . Natomiast w przypadku wyznaczania 8-punktowej DTF (rys. c) próbki widmowe wypadają między zerami widma i przeciek występuje. | *Wykres wyjaśnia dlaczego w przypadku wyznaczenia 6-punktowej DTF (rys. b) nie występuje zjawisko przecieku, tzn. otrzymujemy prawidłowe próbki widma sygnału harmonicznego w punktach <math>\pm \pi/3\,</math> (dla <math>k=\pm 1\,</math> ). Pozostałe próbki widmowe, składające się na DFT, wypadają bowiem dokładnie w punktach zerowych rozmytego widma <math>X_0 (e^{j\theta})</math> . Natomiast w przypadku wyznaczania 8-punktowej DTF (rys. c) próbki widmowe wypadają między zerami widma i przeciek występuje. | ||
*Zjawisko przecieku objawia się w podobny sposób w przypadku, gdy w skończonym oknie czasowym są obserwowane sygnały nieokresowe. Energia (lub moc) sygnału przecieka wówczas nie do obcych prążków, ale w inne ciągłe przedziały osi <math>\theta\,</math> . | *Zjawisko przecieku objawia się w podobny sposób w przypadku, gdy w skończonym oknie czasowym są obserwowane sygnały nieokresowe. Energia (lub moc) sygnału przecieka wówczas nie do obcych prążków, ale w inne ciągłe przedziały osi <math>\theta\,</math> . | ||
| Linia 149: | Linia 149: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd15.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd15.png]] | ||
|valign="top"| | |valign="top"| | ||
*Schemat motylkowy algorytmu STF przedstawiony na rysunku został sporządzony dla przypadku <math>N=8=2^3</math> . Ponieważ w ogólnym przypadku schemat motylkowy składa się z | *Schemat motylkowy algorytmu STF przedstawiony na rysunku został sporządzony dla przypadku <math>N=8=2^3</math> . Ponieważ w ogólnym przypadku schemat motylkowy składa się z <math>log_2 N\,</math> kolumn (poziomów), z których każdy zawiera <math>N/2\,</math> motylków, więc dla <math>N=8</math> mamy 3 kolumny po 4 motylki. | ||
*Danymi wejściowymi algorytmu są próbki sygnału <math>x(n)\,</math> (w podanym przykładzie 8 próbek dla <math>n=0,...,7\,</math> ) oraz znane liczby zespolone o postaci <math>W_{2^m} | *Danymi wejściowymi algorytmu są próbki sygnału <math>x(n)\,</math> (w podanym przykładzie 8 próbek dla <math>n=0,...,7\,</math> ) oraz znane liczby zespolone o postaci <math>W_{2^m}^{-j}\,</math> , <math>m=2,3,...\,</math> Na każdym poziomie wykorzystywane są wszystkie próbki <math>x(n)\,</math> , ale w różnej kolejności. | ||
*Na wyjściach poszczególnych motylków otrzymujemy próbki widmowe obliczane na kolejnych poziomach. Na wyjściach motylków ostatniego poziomu otrzymujemy zbiór próbek widmowych składających się na obliczaną DTF (w naszym przypadku 8 próbek). | *Na wyjściach poszczególnych motylków otrzymujemy próbki widmowe obliczane na kolejnych poziomach. Na wyjściach motylków ostatniego poziomu otrzymujemy zbiór próbek widmowych składających się na obliczaną DTF (w naszym przypadku 8 próbek). | ||
*Już dla <math>N=8</math> zysk obliczeniowy jest ponad pięciokrotny. Dla <math>N=10^2=1024</math> zysk ten jest ponad 200-krotny. | *Już dla <math>N=8</math> zysk obliczeniowy jest ponad pięciokrotny. Dla <math>N=10^2=1024</math> zysk ten jest ponad 200-krotny. | ||