PS Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 96: | Linia 96: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd10.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd10.png]] | ||
|valign="top"| | |valign="top"| | ||
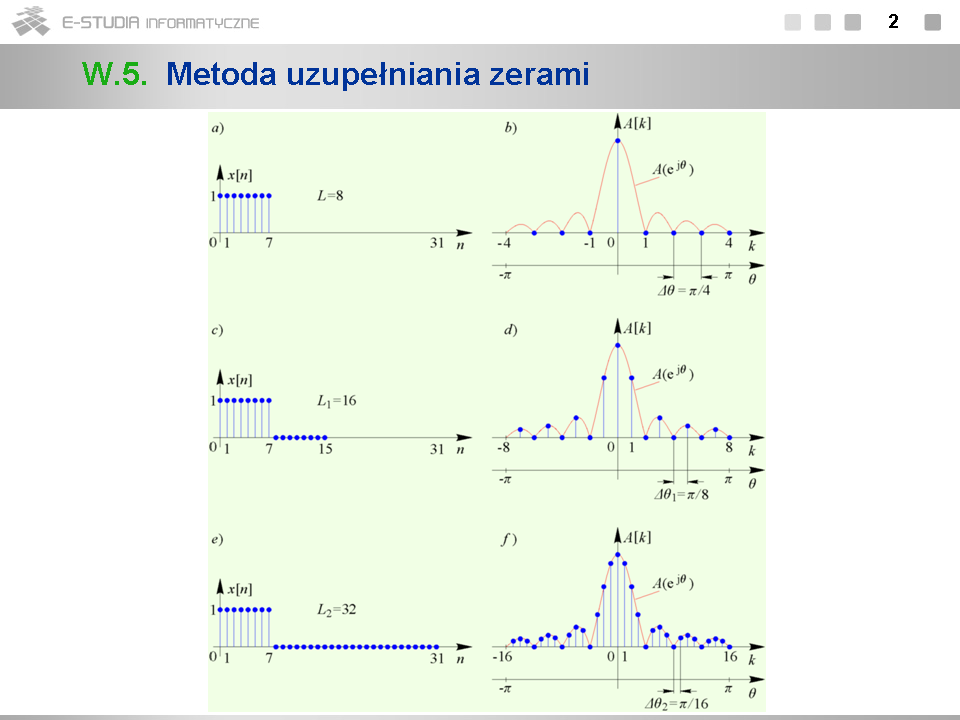
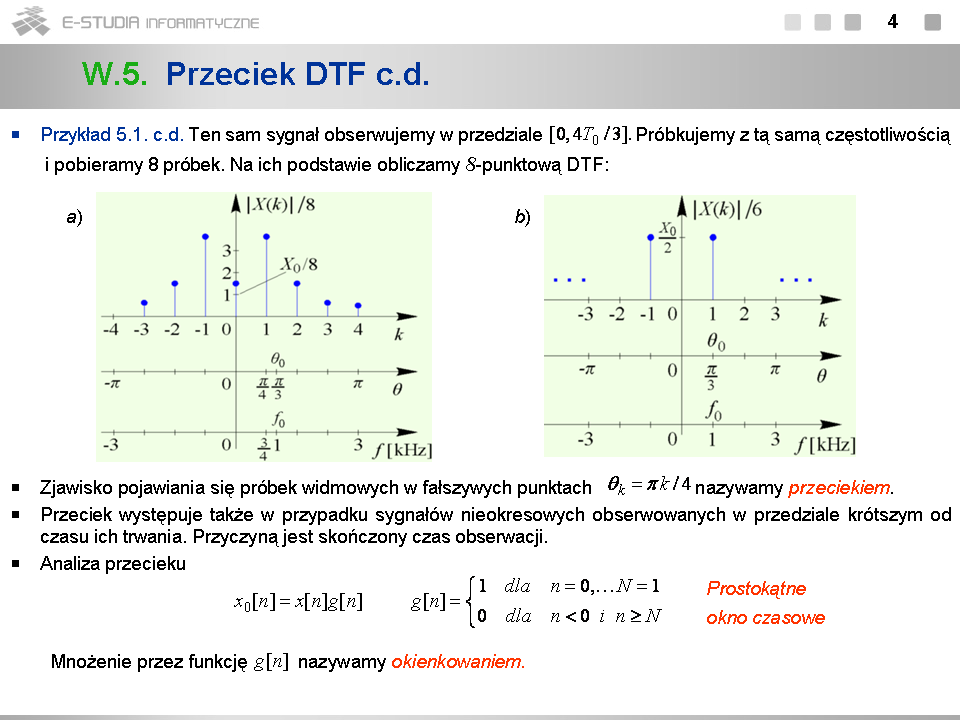
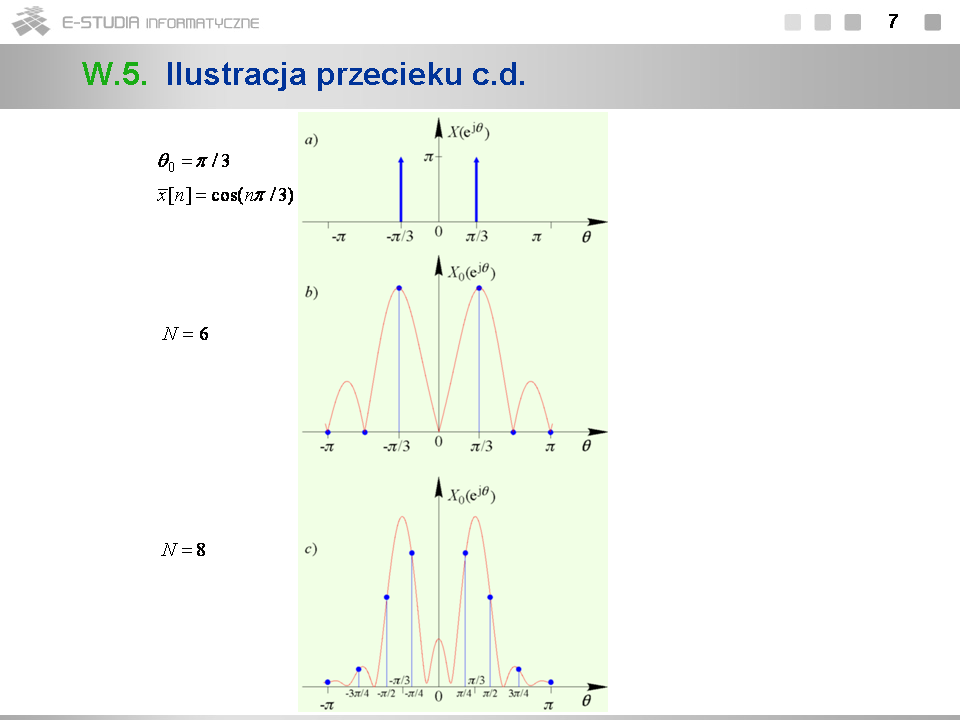
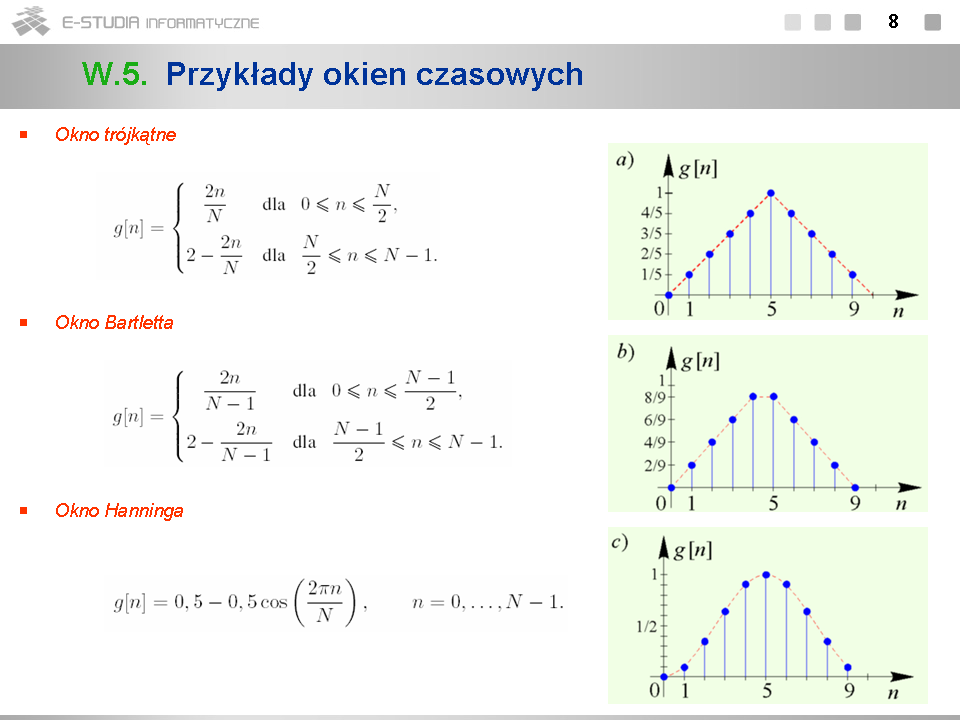
*W szacowaniu złożoności obliczeniowej DTF zakładamy, że sygnał <math>x[n]\,</math> jest zespolony. | |||
*Liczba <math>W=e^{j2\pi/N}</math> ma ciekawe właściwości. Jest ona równa pierwiastkowi <math>N\,</math> -tego z jedności. Jej <math>N\,</math> -ta potęga jest równa jedności: <math>W^n=(e^{j2\pi/N})^N=e^{j2\pi}=1</math> . Ponadto w wyniku próbkowania <math>N\,</math> razy w okresie w chwilach <math>nT_s\,</math> zespolonego sygnału harmonicznego <math>e^{j\omega_0 t}\,</math> otrzymujemy próbki będące kolejnymi potęgami liczby <math>W\, :\, e^{j\omega_0 nT_s}=e^{j2\pi nT_s/T_0}=(e^{j2\pi /N})^n=W^n</math> . | |||
*O złożoności obliczeniowej DTF decyduje liczba mnożeń. Dlatego przy jej szacowaniu nie uwzględnia się dodawań. Liczba mnożeń wynosi dokładnie <math>(N-1)^2\,</math> , gdyż obliczenie próbki widmowej dla <math>k=0</math> wymaga wykonania tylko dodawań. Dla większych <math>N\,</math> można dla prostoty szacowania przyjąć, że liczba mnożeń jest równa <math>N^2\,</math> . | |||
|} | |} | ||
Wersja z 13:27, 5 wrz 2006

|

|

|

|

|