PS Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 32: | Linia 32: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd4.png]] | ||
|valign="top"| | |valign="top"| | ||
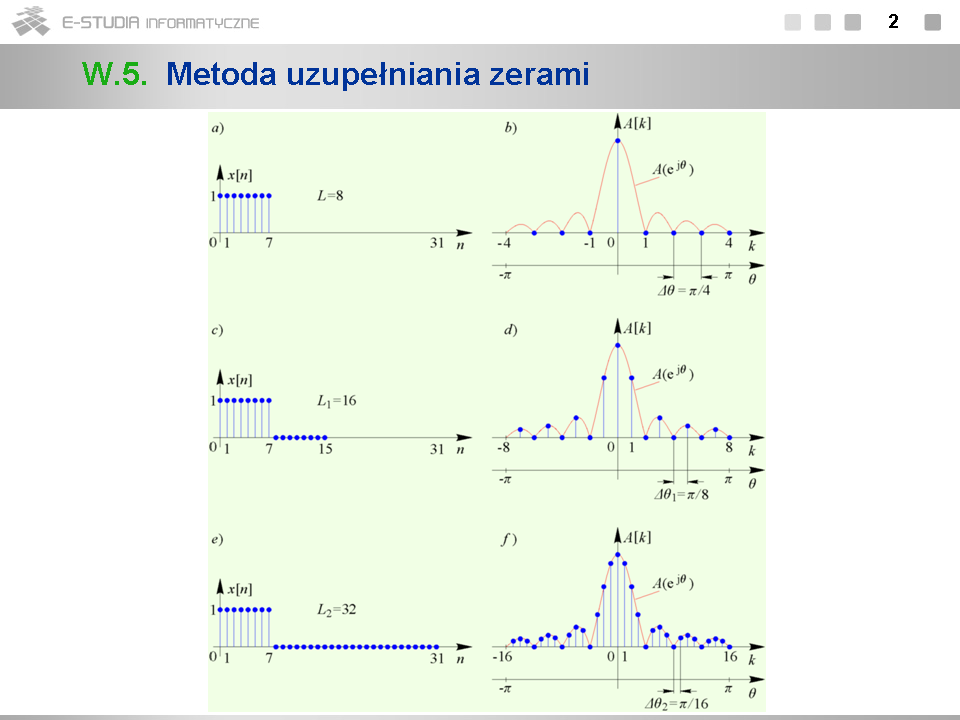
*Punkty <math>\theta_k =\pi k/4</math> odpowiadają częstotliwością nieunormowanym <math>f_k=k\times 0,75\, kHz</math> , nie pokrywającymi się z właściwą częstotliwością sygnału <math>1\, kHz</math> . | |||
*Można mówić o przecieku mocy sygnału skoncentrowanej w prążku widmowym o częstotliwości <math>1\, kHz</math> do prążków widmowych występujących w fałszywych punktach osi częstotliwości. | |||
*Obserwacja sygnału <math>x[n]\,</math> w skończonym przedziale czasu <math>n=N,...,N-1\,</math> odpowiada mnożeniu tego sygnału przez prostokątne okno czasowe. Mówimy wówczas o okienkowaniu sygnału. | |||
|} | |} | ||
| Linia 41: | Linia 43: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd5.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd5.png]] | ||
|valign="top"| | |valign="top"| | ||
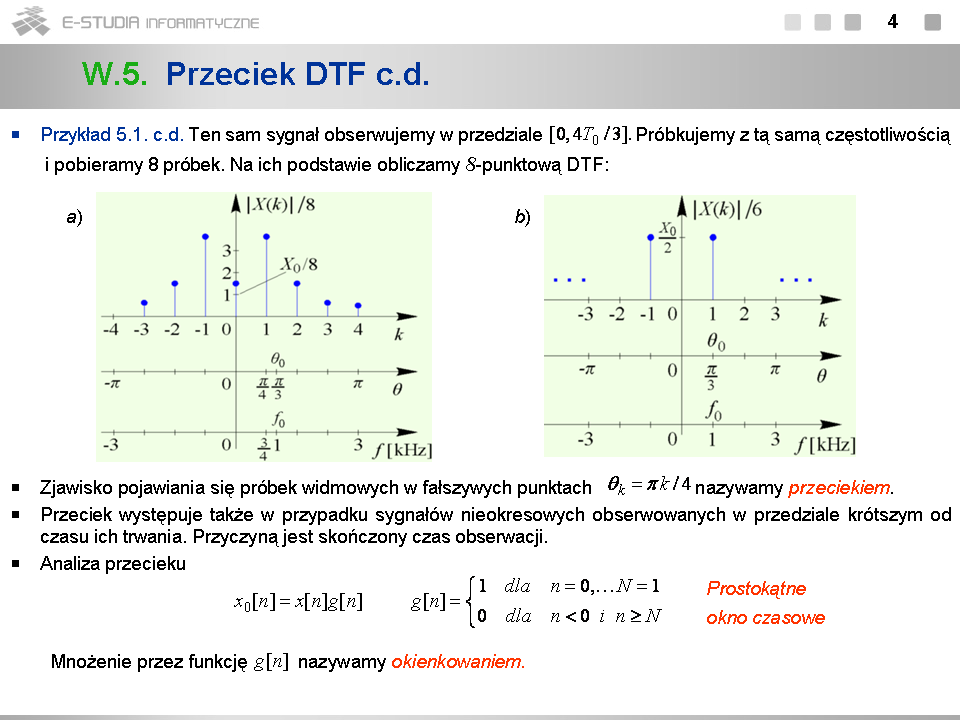
*Obserwacja sygnału <math>x[n]\,</math> w skończonym prostokątnym oknie czasowym <math>g[n]\,</math> odpowiada splataniu widma tego sygnału przez widmo okna opisane wzorem (5.2). | |||
*Na zniekształcenia widma amplitudowego nie ma wpływu czynnik wykładniczy widma (5.2), a decyduje o nich drugi czynnik, którego struktura jest listkowa. | |||
*W przypadku okna prostokątnego stosunek wysokości pierwszego listka bocznego do wysokości listka głównego nie może być mniejszy od <math>0,212\,</math>. | |||
|} | |} | ||
| Linia 49: | Linia 54: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd6.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd6.png]] | ||
|valign="top"| | |valign="top"| | ||
*Przykład 5.2 dobrze ilustruje zjawisko przecieku w przypadku sygnału harmonicznego. Dokładne widmo tego sygnału składa się z (okresowo powtarzanej z okresem <math>2\pi\,</math> ) pary dystrybucji w punktach <math>\pm \theta_0\,</math> (rys. a). Skończony czas obserwacji powoduje, że dystrybucje te rozmywają się na dwa widma listkowe rozmieszczone wokół punktów <math>\pm \theta_0\,</math> . | |||
|} | |} | ||
| Linia 57: | Linia 63: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd7.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd7.png]] | ||
|valign="top"| | |valign="top"| | ||
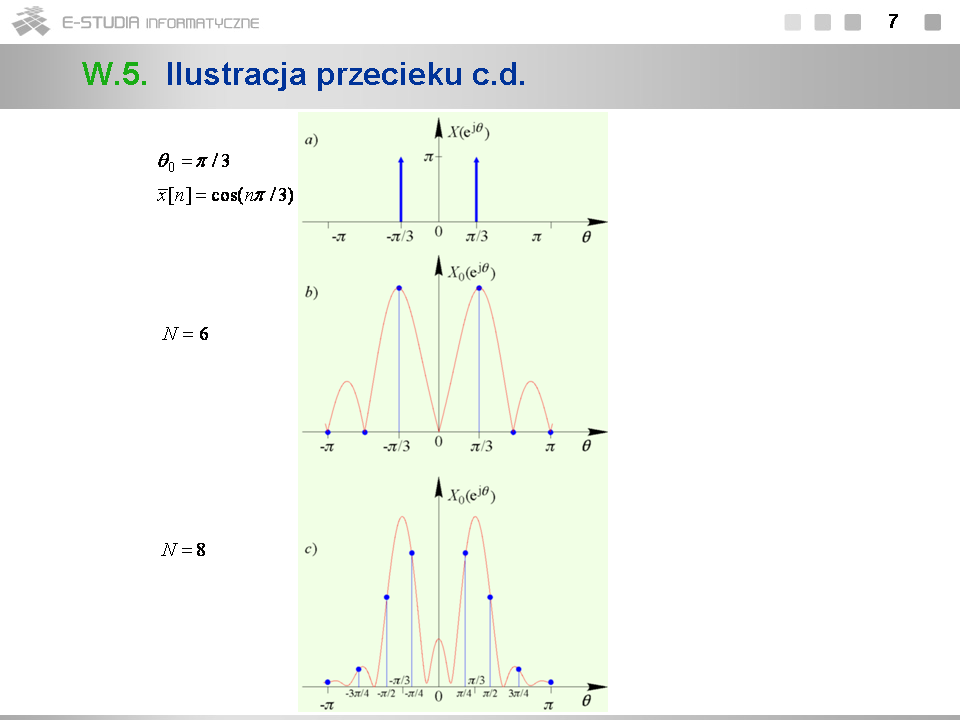
*Na rys. b i c pokazano wykresy widma amplitudowego sygnału harmonicznego z przykładu 5.2 o pulsacji unormowanej <math>\theta_0 =\pi /3</math> okienkowanego oknem prostokątnym w dwóch przypadkach: <math>N=6\,</math> oraz <math>N=8\,</math> . | |||
*Wykres wyjaśnia dlaczego w przypadku wyznaczenia 6-punktowej DTF (rys. b) nie występuje zjawisko przecieku, tzn. otrzymujemy prawidłowe próbki widma sygnału harmonicznego w punktach <math>\pm \pi/3\,</math> (dla <math>k\pm 1\,</math> ). Pozostałe próbki widmowe, składające się na DFT, wypadają bowiem dokładnie w punktach zerowych rozmytego widma <math>X_0 (e^{j\theta})</math> . Natomiast w przypadku wyznaczania 8-punktowej DTF (rys. c) próbki widmowe wypadają między zerami widma i przeciek występuje. | |||
*Zjawisko przecieku objawia się w podobny sposób w przypadku, gdy w skończonym oknie czasowym są obserwowane sygnały nieokresowe. Energia (lub moc) sygnału przecieka wówczas nie do obcych prążków, ale w inne ciągłe przedziały osi <math>\theta\,</math> . | |||
|} | |} | ||
| Linia 65: | Linia 74: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd8.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd8.png]] | ||
|valign="top"| | |valign="top"| | ||
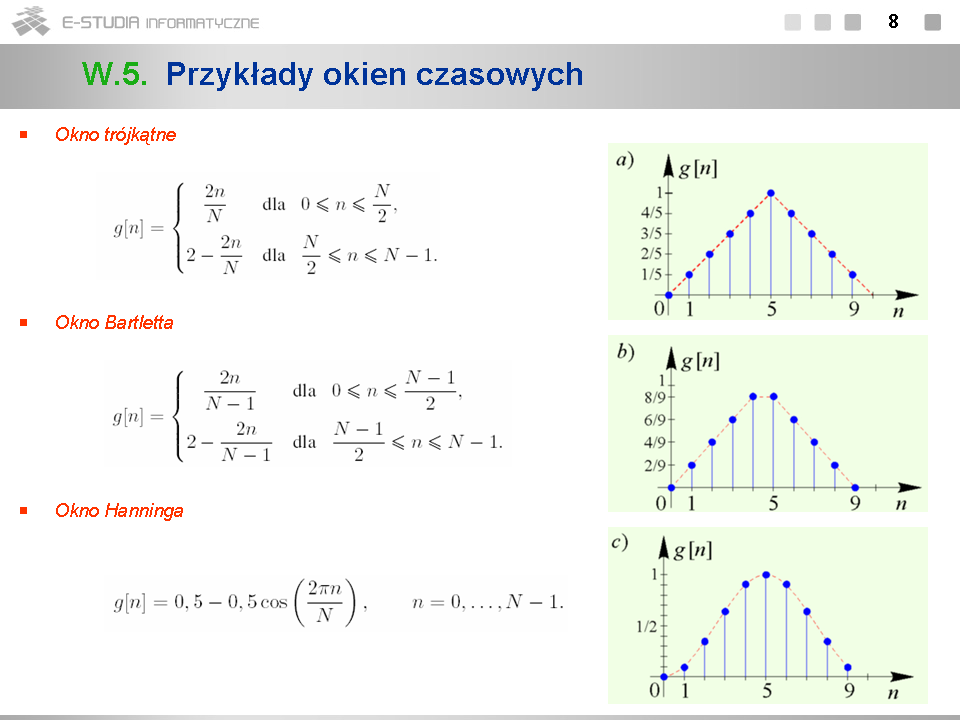
*Widma wszystkich pokazanych na wykresach okien czasowych mają strukturę listkową. Zniekształcenia widma sygnału spowodowane skończonym czasem jego obserwacji są tym mniejsze im mniejszy jest poziom listków bocznych i jednocześnie węższy jest listek główny. Wymagania te są jednak sprzeczne. | |||
*Dobierając inne od prostokątnego okna czasowe, zmniejszamy poziom listków bocznych. Powoduje to jednak jednoczesny wzrost szerokości listka głównego. | |||
*Na wykresach pokazano przykłady okien czasowych różnych od prostokątnego dla przypadku <math>N=10\,</math> . | |||
|} | |} | ||
| Linia 73: | Linia 85: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd9.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd9.png]] | ||
|valign="top"| | |valign="top"| | ||
*Zauważmy, że obie krańcowe wartości okna Hamminga (rys. e) są różne od zeru (równe <math>0,08\,</math>). Ta drobna różnica powoduje, że poziom listków bocznych jest dla tego okna mniejszy w porównaniu np. z oknem Hanna (rys. d) lub oknem Blackmana (rys. f). | |||
*W porównaniu z oknem prostokątnym wszystkie okna pokazane na rys. a-f zapewniają mniejszy poziom listków bocznych, ale kosztem wzrostu szerokości listka głównego. Dla okien tych wielkości te przy zadanym <math>N\,</math> są ustalone i nie można na nie wpływać. Istnieją jednak bardziej złożone okna, w których poziom listków bocznych i szerokość listka głównego można regulować i dobierać ich wartości w drodze kompromisu. | |||
*Im poziom listków bocznych widma okna jest mniejszy, tym większa jest tzw. ''rozróżnialność częstotliwościowa'' DTF. Natomiast im szerokość listka głównego jest mniejsza, tym większa jest tzw. ''rozróżnialność amplitudowa'' DTF. | |||
|} | |} | ||
Wersja z 13:17, 5 wrz 2006

|

|

|

|

|

|