PS Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 12: | Linia 12: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd2.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd2.png]] | ||
|valign="top"| | |valign="top"| | ||
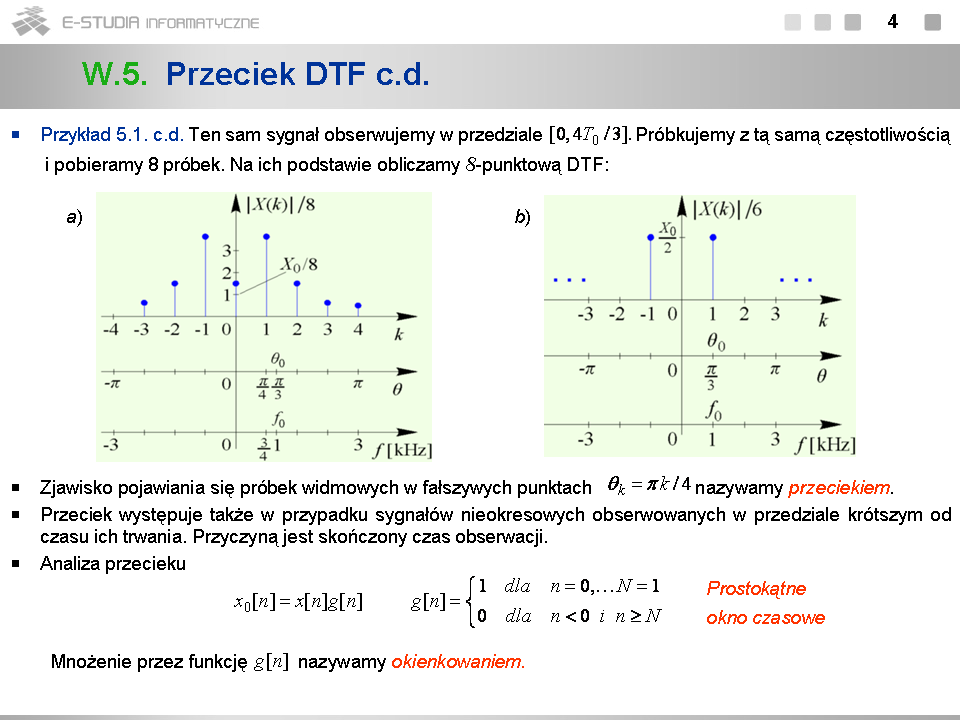
*Dodanie do ośmiu właściwych próbek sygnału ośmiu dodatkowych próbek zerowych zwiększa rozdzielczość DTF dwukrotnie. | |||
*Próbki widmowe leżą zawsze na krzywej ciągłej <math>A(e^{j\theta})\,</math> . | |||
*Wraz ze wzrostem dodatkowych zer wzrasta nakład obliczeniowy. | |||
|} | |} | ||
| Linia 20: | Linia 23: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd3.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd3.png]] | ||
|valign="top"| | |valign="top"| | ||
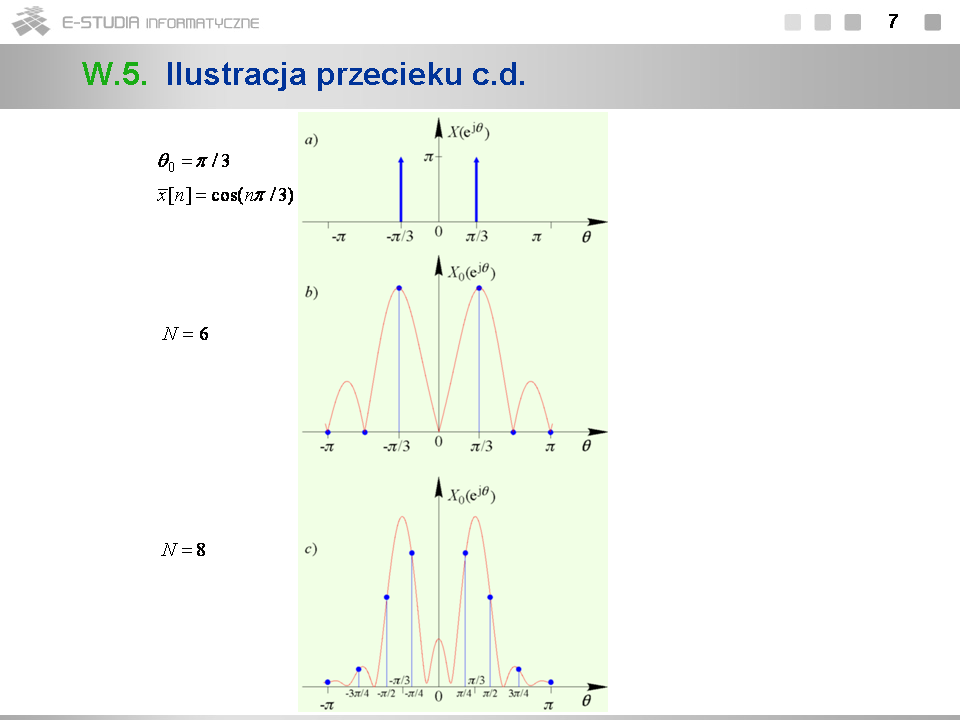
*Zgodnie z właściwością symetrii wystarczy obliczyć tylko próbki widmowe <math>X(0), X(1), X(2), X(3)\,</math> . Jak widzimy tylko próbki <math>X(1)\,</math> i <math>X(5)\,</math> (lub równoważnie <math>X(-1)\,</math> ) są niezerowe. | |||
*Gdy analogowy sygnał harmoniczny jest obserwowany dokładnie tylko przez jeden jego okres, wówczas DTF wyznaczone na podstawie jego próbek daje prawidłowy obraz jego widma. Niezerowe próbki widmowe otrzymujemy tylko dla pulsacji unormowanych <math>\theta\pm \pi/3\,</math> odpowiadających częstotliwościom nieunormowanym <math>f=\pm 1\, kHz</math> . | |||
|} | |} | ||
| Linia 28: | Linia 32: | ||
|width="500px" valign="top"|[[Grafika:PS_M5_Slajd4.png]] | |width="500px" valign="top"|[[Grafika:PS_M5_Slajd4.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
Wersja z 12:58, 5 wrz 2006
|
|

|

|
|
|

|

|

|

|

|

|

|