MN05LAB: Różnice pomiędzy wersjami
mNie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 4: | Linia 4: | ||
--> | --> | ||
=Ćwiczenia: | =Ćwiczenia: rozwiązywanie układów równań liniowych= | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Mnożyć przez odwrotność to nie zawsze to samo...</span> | ||
<div class="exercise"> | <div class="exercise"> | ||
W Octave układ równań <math>\displaystyle Ax=b</math> rozwiązujemy korzystając z "operatora | |||
<math>\displaystyle A=( | rozwiązywania równania" | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
x = A \ b; | |||
</pre></div> | |||
W tym celu Octave oczywiście wewenętrznie wykorzystuje funkcję LAPACKa | |||
<code>DGESV</code>. Ale w Octave jest także funkcja <code>inv</code>, wyznaczająca macierz | |||
odwrotną, więc niektóre (nie najlepsze, oględnie mówiąc) podręczniki zalecają | |||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
x = inv(A)*b; | |||
</pre></div> | |||
Przedyskutuj, które podejście jest lepsze i dlaczego. Przeprowadź eksperymenty | |||
numeryczne weryfikujące Twoją tezę. | |||
</div></div> | |||
< | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | ||
Wyznaczenie <math>\displaystyle A^{-1}</math> praktycznie nigdy nie jest konieczne w obliczeniach, a | |||
</math> | zwłaszcza do rozwiązania układu równań. Nie dość, że jest bardziej kosztowne, to | ||
dodatkowo nie jest numerycznie poprawne. | |||
Przykładowy test mógłby wyglądać w poniższy sposób. Duże macierze losowe są | |||
zazwyczaj dobrze uwarunkowane i najczęściej nieosobliwe. | |||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
N = 400; A = rand(N,N);x = rand(N,1); b = A*x; | |||
tic; X = A \ b; tX = toc; | |||
tic; Y = inv(A)*b; tY = toc; | |||
[norm(X-x)/norm(x), norm(Y-x)/norm(x); tX, tY] | |||
</pre></div> | |||
<div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | |||
ans = | |||
1.9861e-13 2.8687e-13 | |||
2.3644e-01 4.0609e-01 | |||
</pre></div> | |||
Wyszło (z grubsza) dwa razy szybciej i dwa razy dokładniej. | |||
< | </div></div></div> | ||
</ | |||
<div | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Wybór elementu głównego jest naprawdę ważny!</span> | |||
<div class="exercise"> | |||
Rozwiąż prosty układ równań | |||
<center><math>\displaystyle \aligned 10^{-18} x_1 + x_2 &= 1,\\ | |||
x_1 + 2x_2 &= 4, | |||
\endaligned</math></center> | |||
czterema sposobami: | |||
* na kartce papieru (dokładnie!) | |||
* w komputerze, w arytmetyce podwójnej precyzji, korzystając z rozkładu LU <strong>bez wyboru elementu głównego</strong> | |||
* jak poprzednio, ale <strong>z wyborem elementu głównego w kolumnie</strong> | |||
< | * w LAPACKu lub Octave. | ||
Porównaj uzyskane rozwiązania i wyciągnij wnioski. | |||
</div></div> | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | |||
Rozwiązanie uzyskane bez wyboru elementu głównego jest bardzo mało precyzyjne <math>\displaystyle x_1</math> jest obarczone bardzo duzym błędem! Prosta analiza poazuje, że winę za to ponosi bardzo wielki współczynnik w macierzy <math>\displaystyle L</math>. Tak nie jest, gdy stosujemy wybór elementu: elementy <math>\displaystyle L</math> są zawsze mniejsze od 1. Dlatego inne rozwiązania numeryczne dają w przypadku naszej macierzy wynik, będący bardzo dobrym przybliżeniem wyniku dokładnego. ''A propos:'' Octave korzysta z <code>DGESV</code> LAPACKa, a <code>DGESV</code> korzysta z wyboru w kolumnie... | |||
</div></div></div> | </div></div></div> | ||
| Linia 55: | Linia 83: | ||
<div class="exercise"> | <div class="exercise"> | ||
Zapisz w Octave algorytm rozkładu LU macierzy (bez wyboru elementu głównego) działający ''in situ''. | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
<div style="font-size:smaller; background-color:#efe"> | <div style="font-size:smaller; background-color:#efe"> Pamiętaj, pętle w Octave wykonują się bardzo wolno! </div> | ||
</div></div> | </div></div> | ||
Wykorzystaj go do napisania funkcji, która rozwiąże układ równań <math>\displaystyle Ax=b</math>. | |||
Przetestuj tę funkcję na kilku macierzach i porównaj czas jego działania z czasem | |||
wykonania operacji <code>x = A\b</code>. | |||
Spróbuj zastosować swój algorytm do kilku specjalnych macierzy: | |||
* Hilberta dużego wymiaru | |||
* diagonalnej z jednym elementem bardzo małym (a nawet równym zero) | |||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | ||
Najprostszy wariant to po prostu przepisanie algorytmu z wykładu, który już | |||
< | nawet trochę wykorzystywał notację dwukropkową MATLABa: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
</math></ | |||
function [L,U] = lufa(A) | |||
# Na początku warto dodać trochę sprawdzania danych: czy A jest kwadratowa? a w ogóle, | |||
# czy jest macierzą? te linie pozostawiamy inwencji Czytelnika | |||
N = size(A,1); | |||
for k=1:N-1 | |||
if (A(k,k) == 0.0) | |||
return; | |||
end | |||
for i=k+1:N #wyznaczenie <math>\displaystyle k</math>-tej kolumny <math>\displaystyle L</math> | |||
A(i,k) = A(i,k)/A(k,k); | |||
end | |||
for j=k+1:N #modyfikacja podmacierzy <math>\displaystyle A_{22} = A_{22} - l_{21}u_{12}^T</math> | |||
for i=k+1:N | |||
A(i,j) -= A(i,k)*A(k,j); | |||
end | |||
end | |||
end | |||
L = tril(A,-1) + eye(N); | |||
U = triu(A); | |||
end | |||
</pre></div> | |||
Jednak w tej implementacji mamy do czynienia z nawet potójnie zagnieżdżonymi | |||
pętlami, co dla nawet średnich <math>\displaystyle N</math> może być powodem sporego spowolnienia | |||
algorytmu. Warto więc uniknąć pętli, odwołując się do instrukcji wektorowych i | |||
blokowych. | |||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
function [L,U] = lufb(A) | |||
# Na początku warto dodać trochę sprawdzania danych: czy A jest kwadratowa? a w ogóle, | |||
# czy jest macierzą? te linie pozostawiamy inwencji Czytelnika | |||
N = size(A,1); | |||
for k=1:N-1 | |||
if (A(k,k) == 0.0) | |||
return; | |||
end | |||
#wyznaczenie <math>\displaystyle k</math>-tej kolumny <math>\displaystyle L</math> | |||
A(k+1:N,k) = A(k+1:N,k)/A(k,k); | |||
#modyfikacja podmacierzy <math>\displaystyle A_{22} = A_{22} - l_{21}u_{12}^T</math> | |||
A(k+1:N,k+1:N) -= A(k+1:N,k)*A(k,k+1:N); | |||
end | |||
L = tril(A,-1) + eye(N); | |||
U = triu(A); | |||
end | |||
</pre></div> | |||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
[Kod testujący lufa(0 i lufb()] | |||
N = 100; | |||
A = rand(N) + 1000*eye(N); | |||
format short e; | |||
t = ta = tb = Inf; | |||
K = 5; | |||
for i = 0:K | |||
tic; [L, U] = lu(A); t = min(t,toc); | |||
tic; [La, Ua] = lufa(A); ta = min(ta,toc); | |||
tic; [Lb, Ub] = lufb(A); tb = min(tb,toc); | |||
end | |||
disp("Czasy: lu(), lufa(), lufb()"); [t, ta, tb] | |||
disp("Błąd:"); | |||
[norm(L*U - A,inf), norm(La*Ua - A,inf), norm(Lb*Ub - A,inf)] | |||
</pre></div> | |||
Dla macierzy wymiaru <math>\displaystyle N=100</math> dostaliśmy na Pentium 1.5GHz | |||
{| border=1 | |||
|+ <span style="font-variant:small-caps"> </span> | |||
|- | |||
| Implementacja || lu (oryginalne) || lufa || lufb | |||
|- | |||
| Czas (s) || 4.0436e-03 || 1.5877e+01 || 1.0767e-01 | |||
|- | |||
| Błąd <math>\displaystyle ||LU-A||_\infty</math> || 3.4596e-13 || 8.0747e-13 || 8.0747e-13 | |||
|} | |||
Zwróć uwagę na charakterystyczne fakty: | |||
* Usunięcie wewnętrznych pętli stukrotnie(!) przyspieszyło <code>lufb</code> w | |||
stosunku do <code>lufa</code> | |||
* Gotowa funkcja Octave wciąż jest stukrotnie(!) szybsza od mojej | |||
najszybszej funkcji. | |||
To jest typowe, gdy korzystamy ze środowisk typu Octave czy MATLAB. Czasem | |||
nawet lepiej napisać implementację wykonującą więcej obliczeń, ale korzystającą | |||
w większm stopniu z wbudowanych funkcji Octave, niż napisać samemu implementację | |||
liczącą mniej, ale korzystającą z licznych instrukcji <code>for...</code> i podobnych. | |||
Innym sposobem przyspieszenia działania funkcji Octave jest ich prekompilacja. | |||
To w znacznym stopniu usuwa problemy związanie z korzystaniem z pętli, ale | |||
wykracza poza zakres naszego kursu. | |||
Funkcja wykorzystująca gotowy rozkład LU do rozwiązania układu <math>\displaystyle Ax=b</math> w MATLABie miałaby postać | |||
</math> | |||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | |||
function x = sol(L,U,b) | |||
x = U \ ( L \ b); | |||
end | |||
</pre></div> | |||
gdyż MATLAB prawidłowo rozpoznaje układy z macierzą trójkątną i stosuje szybszy | |||
algorytm. Niestety, do tej pory w Octave nie jest to możliwe; nie ma też | |||
funkcji, która rozwiązywałaby układ z macierzą trójkątną (wykorzystując np. | |||
LAPACKa). Zrób więc to i... wyślij do twórców Octave'a! | |||
</div></div></div> | </div></div></div> | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Czy Twoje programy działają <strong>naprawdę</strong> szybko?</span> | ||
<div class="exercise"> | <div class="exercise"> | ||
Zrób zadanie poprzednie programując, niczym Zosia-Samosia, wszystko od początku do końca w czystym C. Porównaj czasy działania Twojego programu i programu wywołującego po prostu procedurę biblioteczną LAPACKa | |||
< | <code>DGESV</code>, najlepiej wspartą dobrze podrasowanymi BLASami. | ||
< | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
</ | <div style="font-size:smaller; background-color:#efe"> To zadanie to wyzwanie! </div> | ||
</div></div> | |||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | |||
No tak, namawiamy Cię do zmierzenia się z LAPACKiem i ATLASem.... | |||
Prościutki program --- po prostu tłumaczącu algorytm z wykładu bezpośrednio | |||
na C --- u nas spisał | |||
się, dla macierzy wymiaru <math>\displaystyle N=1\ldots 1024</math>, następująco: | |||
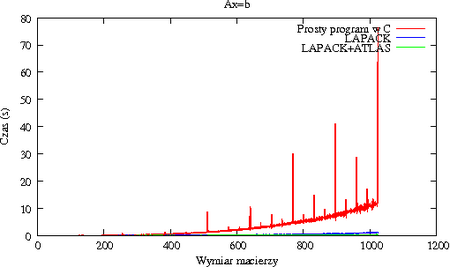
[[Image:MNdegsvtiming.png|thumb|450px|center|Prosty solver w C kontra LAPACK i LAPACK z ATLASem. | |||
Zwróć uwagę na piki zwykłego kodu dla <math>\displaystyle N</math> będących potęgami dwójki]] | |||
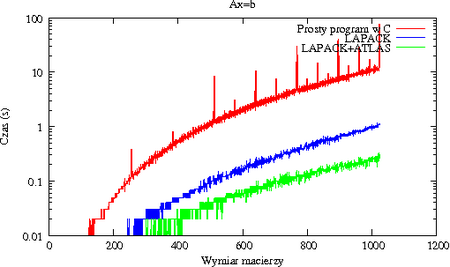
[[Image:MNdegsvtiminglogscale.png|thumb|450px|center|Skala logarytmiczna pozwala lepiej ocenić | |||
różnice pomiędzy czasami wykonania. Prosty program w C jest około dziesięć razy | |||
wolniejszy od kodu korzystającego z LAPACKa i około 50 razy wolniejszy od kodu | |||
korzystającego z LAPACKa i ATLASa.]] | |||
</div></div></div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Układy równań z wieloma prawymi stronami</span> | ||
<div class="exercise"> | <div class="exercise"> | ||
Podaj sposób taniego wyznaczenia rozwiązania sekwencji <math>\displaystyle k<N</math> układów równań z tą | |||
<math>\displaystyle | samą macierzą <math>\displaystyle A\in R^{N\times N}</math> i różnymi prawymi stronami: | ||
<center><math>\displaystyle | |||
<center><math>\displaystyle | Ax_i = b_i, \qquad i = 1,\ldots,k. | ||
</math></center> | </math></center> | ||
Układy równań z tą samą macierzą, ale ze zmieniającą się prawą stroną równania | |||
powstają często przy rozwiązywaniu, np. równań różniczkowych cząstkowych, | |||
gdzie prawa strona układu odpowiada zmieniającym się warunkom brzegowym. | |||
< | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
<div style="font-size:smaller; background-color:#efe"> Wystarczy tylko <strong>jeden raz</strong> wyznaczyć rozkład LU macierzy <math>\displaystyle A</math> </div> | |||
</ | </div></div> | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | |||
No tak, oczywiście, | |||
wystarczy | |||
{{algorytm||| | |||
<pre> | |||
Znajdź rozkład <math>\displaystyle PA = LU</math>; | |||
Utwórz macierz <math>\displaystyle B = [b_1,\ldots,b_k]</math>; | |||
Rozwiąż <math>\displaystyle LY = B</math>; | |||
Rozwiąż <math>\displaystyle UX = Y</math>; | |||
</pre>}} | |||
Rozwiązanie każdego z układów <math>\displaystyle LY = B</math> i <math>\displaystyle UX = Y</math> można przyspieszyć, tworząc | |||
warianty algorytmów podstawienia w przód i w tył, operujące od razu na wszystkich kolumnach macierzy <math>\displaystyle B</math>. Zaimplementowano je w LAPACKu, w tandemie | |||
funkcji <code>DGETRF</code> (rozkład) i <code>DGETRS</code> (rozwiązanie) oraz w | |||
<code>DGESV</code>, łączącej funkcjonalność obu. | |||
</div></div></div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie</span> | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Metoda Cholesky'ego</span> | ||
<div class="exercise"> | <div class="exercise"> | ||
Ważnym przykładem macierzy | |||
szczególnej postaci są macierze symetryczne i dodatnio określone. | |||
Są to macierze spełniające warunki: | |||
< | <center><math>\displaystyle A=A^T \qquad \mbox{oraz} \qquad x^T A x\,>\,0,\quad\forall x\ne 0. | ||
< | </math></center> | ||
</ | |||
Dla takich macierzy można nieco zmniejszyć koszt kombinatoryczny | |||
i zużycie pamięci przeprowadzając trochę inny rozkład na macierze trójkątne: | |||
tak, aby otrzymać | |||
rozkład | |||
<center><math>\displaystyle A\,=\,L\cdot D\cdot L^T | |||
</math></center> | |||
zamiast <math>\displaystyle PA=LU</math>, przy czym <math>\displaystyle L</math> jest tu jak zwykle macierzą | |||
trójkątną dolną z jedynkami na przekątnej, a <math>\displaystyle D</math> jest macierzą | |||
diagonalną z dodatnimi elementami na diagonali. Opracuj taki algorytm. W jego | |||
implementacji możesz porównywać się z procedurą LAPACKa <code>DPOSV</code>. | |||
Inny wariant tego samego | |||
rozkładu to tak zwany rozkład Cholesky'ego--Banachiewicza, w którym przy tych | |||
samych założeniach na <math>\displaystyle A</math>, szukamy rozkładu wykorzystującego tylko jedną macierz | |||
trójkątną dolną: | |||
<center><math>\displaystyle A\,=\,\widetilde{L}\cdot \widetilde{L}^T, | |||
</math></center> | |||
(oczywiście tym razem nie żądamy, aby <math>\displaystyle \widetilde{L}</math> miała na diagonali jedynki). | |||
Jaka jest relacja między rozkładem <math>\displaystyle LDL^T</math> a <math>\displaystyle \widetilde{L}\widetilde{L}^T</math>? | |||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | ||
Bez zmniejszenia ogólności rozpatrzymy | |||
tylko pierwszy krok rozkładu <math>\displaystyle LDL^T</math>. W tym celu, zauważmy najpierw, że | |||
<math>\displaystyle a_{1,1}= e_1^TA e_1>0</math> (gdzie <math>\displaystyle e_1</math> jest pierwszym | |||
wersorem), a więc nie musimy przestawiać wierszy, | |||
bo element na diagonali jest niezerowy. W pierwszym kroku mnożymy | |||
macierz <math>\displaystyle A</math> z lewej strony przez odpowiednią macierz <math>\displaystyle L_1</math>, a potem | |||
z prawej przez <math>\displaystyle L_1^T</math>. Kluczem do zrozumienia algorytmu jest uwaga, | |||
że efektem mnożenia macierzy <math>\displaystyle L_1 A</math> z prawej strony przez <math>\displaystyle L_1^T</math> | |||
jest wyzerowanie elementów pierwszego wiersza poza <math>\displaystyle a_{1,1}</math> | |||
i pozostawienie niezmienionych pozostałych elementów. Ponadto | |||
macierz <math>\displaystyle A^{(1)}=L_1 AL_1^T</math> jest symetryczna i dodatnio określona. | |||
Rzeczywiście, | |||
<center><math>\displaystyle \Big(A^{(1)}\Big)^T\,=\,(L_1AL_1^T)^T | |||
\,=\,(L_1^T)^TA^TL_1^T\,=\,L_1AL_1^T, | |||
</math></center> | |||
<center><math>\displaystyle \ | oraz dla <math>\displaystyle x\ne 0</math> | ||
<center><math>\displaystyle x^T A^{(1)} x\,=\, x^T L_1 A L_1^T x | |||
\,=\,(L_1^T x)^T A(L_1^T x)\,>\,0, | |||
</math></center> | </math></center> | ||
bo <math>\displaystyle x\ne 0</math> implikuje <math>\displaystyle L_1^T x\ne 0</math>. Stąd | |||
<math>\displaystyle | <math>\displaystyle a^{(1)}_{2,2}= e_2^TA^{(1)} e_2>0</math>. Postępując tak | ||
dalej otrzymujemy | |||
<center><math>\displaystyle | <center><math>\displaystyle L_{n-1}L_{n-2}\cdots L_2L_1AL_1^TL_2^T\cdots L_{n-2}^TL_{n-1}^T | ||
\,=\,D, | |||
</math></center> | </math></center> | ||
a więc < | przy czym macierz <math>\displaystyle D</math> jest diagonalna i dodatnio określona, | ||
a więc wyrazy na diagonali są dodatnie. Oznaczając | |||
<center><math>\displaystyle L\,=\,L_1^{-1}L_2^{-1}\cdots L_{n-1}^{-1} | |||
</math></center> | |||
dostajemy żądany rozkład. | |||
Zauważmy, że przy praktycznej realizacji rozkładu <math>\displaystyle A=LDL^T</math> | |||
wystarczy modyfikować jedynie wyrazy pod i na głównej przekątnej | |||
macierzy wyjściowej, ponieważ, jak zauważyliśmy, wszystkie kolejne | |||
macierze <math>\displaystyle A^{(k)}</math> są symetryczne. Pozwala to zmniejszyć --- w stosunku do | |||
rozkładu LU --- koszt | |||
obliczeniowy o połowę, do <math>\displaystyle 2n^3/3</math> operacji arytmetycznych i zmieścić czynniki | |||
rozkładu w pamięci przeznaczonej na przechowywanie istotnych elementów <math>\displaystyle A</math> | |||
(czyli w dolnym trójkącie macierzy). | |||
Oczywiście, <math>\displaystyle \widetilde{L} = L \sqrt{D}</math>. | |||
</div></div></div> | </div></div></div> | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: | <span style="display: block; background-color:#fefeee; border-bottom: 1px solid #E5E5E5; line-height: 1.1em; padding-bottom: 0.2em; font-variant:small-caps; color:#1A6ABF;">Ćwiczenie: Obliczanie wyznacznika macierzy</span> | ||
<div class="exercise"> | <div class="exercise"> | ||
Bardzo rzadko w praktyce numerycznej zdarza się potrzeba obliczenia wartości | |||
wyznacznika macierzy <math>\displaystyle A \in R^{N \times N}</math>. Zaproponuj metodę obliczania | |||
<math>\displaystyle \mbox{det} (A)</math> oraz wskaż, jakiego rodzaju problemy numeryczne możesz napotkać. | |||
</div></div> | |||
<center><math>\displaystyle | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><div style="margin-left:1em"> | ||
Wystarczy wykonać rozkład <math>\displaystyle PA=LU</math>. Wtedy | |||
<center><math>\displaystyle \mbox{det} A\,=\,(-1)^p u_{11}u_{22}\cdots u_{nn}, | |||
</math></center> | </math></center> | ||
gdzie <math>\displaystyle | gdzie <math>\displaystyle p</math> jest liczbą przestawień wierszy w eliminacji. Tak więc, koszt | ||
to | obliczenia wyznacznika to <math>\displaystyle O(N^3)</math>. | ||
Kłopoty numeryczne możemy mieć z reprezentacją samej wartości wyznacznika w | |||
arytmetyce zmiennoprzecinkowej. Ponieważ | |||
<center><math>\displaystyle | <center><math>\displaystyle \mbox{det} (cA) = c^N A, | ||
</math></center> | </math></center> | ||
to dość łatwo będzie trafić (przy większych niż średnich wartościach <math>\displaystyle N</math>) na wartości | |||
wyznacznika, które będą albo potwornie duże, albo potwornie małe. Zresztą, zrób | |||
eksperyment: | |||
Najpierw z losową macierzą <math>\displaystyle 100\times 100</math> i jej krotnościami... | |||
<div class=" | <div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | ||
octave:26> A=rand(100); | |||
octave:27> det(A) | |||
ans = -7.5240e+24 | |||
octave:28> det(10*A) | |||
ans = -7.5240e+124 | |||
octave:29> det(100*A) | |||
ans = -7.5240e+224 | |||
octave:30> det(1000*A) | |||
ans = -Inf | |||
</pre></div> | |||
oraz z coraz większymi macierzami losowymi: | |||
</div></div> | <div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | ||
octave:32> det(rand(100)) | |||
ans = 4.3751e+25 | |||
octave:33> det(rand(400)) | |||
ans = -3.0348e+218 | |||
octave:34> det(rand(800)) | |||
ans = -Inf | |||
</pre></div> | |||
Można sobie z | |||
tym poradzić, szacując wpierw rząd wielkości wyznacznika, a następnie | |||
reprezentując jego wartość w formie cecha--mantysa, np. jako parę liczb <math>\displaystyle m,c</math> | |||
takich, że <math>\displaystyle \mbox{det} (A) = m\cdot 10^c</math>, ale | |||
dopasowując obie tak, by nie nastąpił ani nadmiar, ani niedomiar. | |||
</div></div></div> | |||
Wersja z 17:11, 2 wrz 2006
Ćwiczenia: rozwiązywanie układów równań liniowych
Ćwiczenie: Mnożyć przez odwrotność to nie zawsze to samo...
W Octave układ równań rozwiązujemy korzystając z "operatora rozwiązywania równania"
x = A \ b;
W tym celu Octave oczywiście wewenętrznie wykorzystuje funkcję LAPACKa
DGESV. Ale w Octave jest także funkcja inv, wyznaczająca macierz
odwrotną, więc niektóre (nie najlepsze, oględnie mówiąc) podręczniki zalecają
x = inv(A)*b;
Przedyskutuj, które podejście jest lepsze i dlaczego. Przeprowadź eksperymenty numeryczne weryfikujące Twoją tezę.
Ćwiczenie: Wybór elementu głównego jest naprawdę ważny!
Rozwiąż prosty układ równań
czterema sposobami:
- na kartce papieru (dokładnie!)
- w komputerze, w arytmetyce podwójnej precyzji, korzystając z rozkładu LU bez wyboru elementu głównego
- jak poprzednio, ale z wyborem elementu głównego w kolumnie
- w LAPACKu lub Octave.
Porównaj uzyskane rozwiązania i wyciągnij wnioski.
Ćwiczenie
Zapisz w Octave algorytm rozkładu LU macierzy (bez wyboru elementu głównego) działający in situ.
Wykorzystaj go do napisania funkcji, która rozwiąże układ równań .
Przetestuj tę funkcję na kilku macierzach i porównaj czas jego działania z czasem
wykonania operacji x = A\b.
Spróbuj zastosować swój algorytm do kilku specjalnych macierzy:
- Hilberta dużego wymiaru
- diagonalnej z jednym elementem bardzo małym (a nawet równym zero)
Ćwiczenie: Czy Twoje programy działają naprawdę szybko?
Zrób zadanie poprzednie programując, niczym Zosia-Samosia, wszystko od początku do końca w czystym C. Porównaj czasy działania Twojego programu i programu wywołującego po prostu procedurę biblioteczną LAPACKa
DGESV, najlepiej wspartą dobrze podrasowanymi BLASami.
Ćwiczenie: Układy równań z wieloma prawymi stronami
Podaj sposób taniego wyznaczenia rozwiązania sekwencji układów równań z tą samą macierzą i różnymi prawymi stronami:
Układy równań z tą samą macierzą, ale ze zmieniającą się prawą stroną równania powstają często przy rozwiązywaniu, np. równań różniczkowych cząstkowych, gdzie prawa strona układu odpowiada zmieniającym się warunkom brzegowym.
Ćwiczenie: Metoda Cholesky'ego
Ważnym przykładem macierzy szczególnej postaci są macierze symetryczne i dodatnio określone. Są to macierze spełniające warunki:
Dla takich macierzy można nieco zmniejszyć koszt kombinatoryczny i zużycie pamięci przeprowadzając trochę inny rozkład na macierze trójkątne: tak, aby otrzymać rozkład
zamiast , przy czym jest tu jak zwykle macierzą
trójkątną dolną z jedynkami na przekątnej, a jest macierzą
diagonalną z dodatnimi elementami na diagonali. Opracuj taki algorytm. W jego
implementacji możesz porównywać się z procedurą LAPACKa DPOSV.
Inny wariant tego samego
rozkładu to tak zwany rozkład Cholesky'ego--Banachiewicza, w którym przy tych
samych założeniach na , szukamy rozkładu wykorzystującego tylko jedną macierz
trójkątną dolną:
(oczywiście tym razem nie żądamy, aby miała na diagonali jedynki). Jaka jest relacja między rozkładem a ?
Ćwiczenie: Obliczanie wyznacznika macierzy
Bardzo rzadko w praktyce numerycznej zdarza się potrzeba obliczenia wartości wyznacznika macierzy . Zaproponuj metodę obliczania oraz wskaż, jakiego rodzaju problemy numeryczne możesz napotkać.