PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 272: | Linia 272: | ||
Obie zależności można zapisać w następującej postaci macierzowej | Obie zależności można zapisać w następującej postaci macierzowej | ||
: <math>\begin{bmatrix}U_1\\I_1\end{bmatrix}=\begin{bmatrix}n&0 \\0&\frac{1}{n}\end{bmatrix}\begin{bmatrix}U_2\\I_2\end{bmatrix}</math> | : <math>\begin{bmatrix}U_1\\I_1\end{bmatrix}=\begin{bmatrix}n&0 \\0&\frac{1}{n}\end{bmatrix}\begin{bmatrix}U_2\\I_2\end{bmatrix}</math> | ||
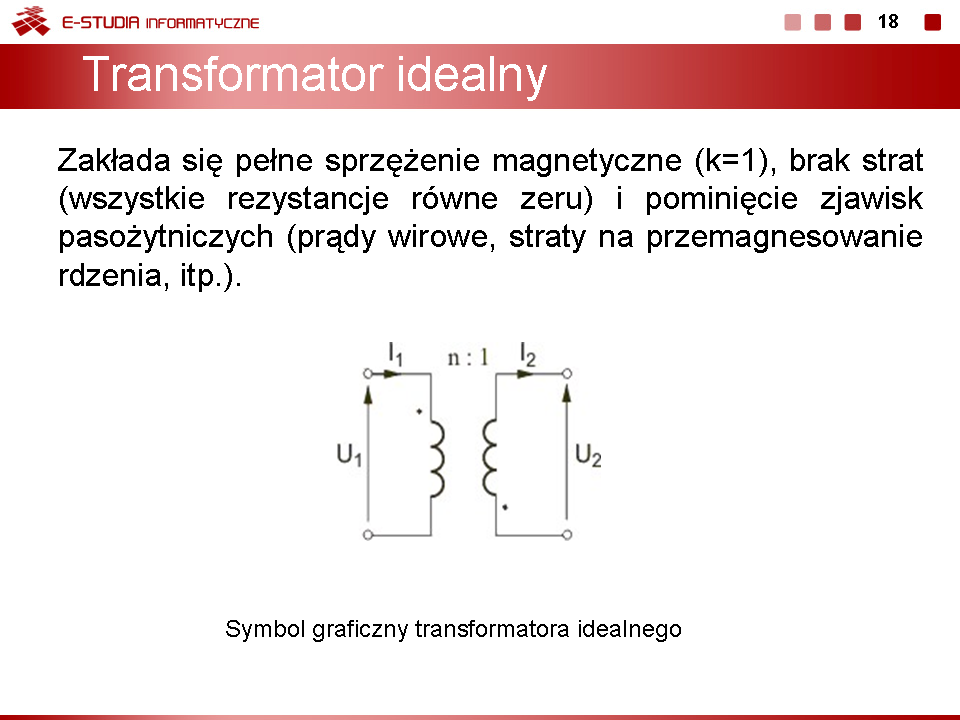
Powyższe równanie macierzowe nazywane jest równaniem łańcuchowym transformatora idealnego. Wykonanie transformatora idealnego w praktyce nie jest możliwe, jednak współczesne realizacje techniczne transformatorów zwłaszcza transformatory z rdzeniem ferromagnetycznym są bliskie ideału. | Powyższe równanie macierzowe nazywane jest równaniem łańcuchowym transformatora idealnego. Wykonanie transformatora idealnego w praktyce nie jest możliwe, jednak współczesne realizacje techniczne transformatorów zwłaszcza transformatory z rdzeniem ferromagnetycznym są bliskie ideału. | ||
| Linia 297: | Linia 295: | ||
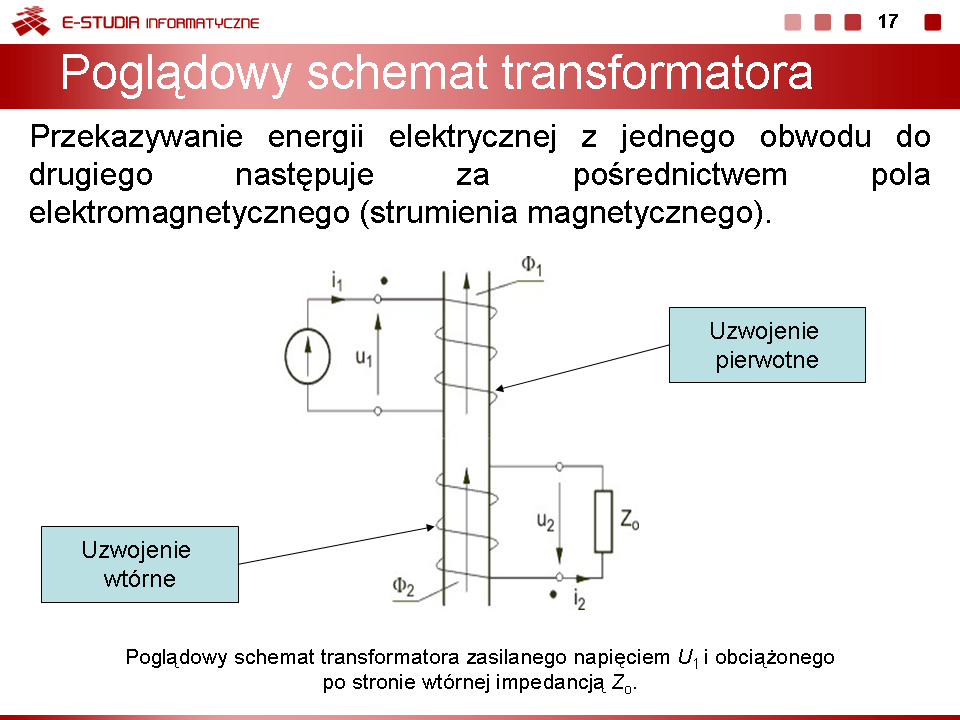
|valign="top"|Analizując transformator w stanie ustalonym przy wymuszeniu sinusoidalnym zastosujemy metodę symboliczną. Z definicji sprzężenia magnetycznego obu cewek przy założonym zwrocie prądów i przyjęciu początków uzwojeń jak na rysunku wynikają następujące równania opisujące obwód | |valign="top"|Analizując transformator w stanie ustalonym przy wymuszeniu sinusoidalnym zastosujemy metodę symboliczną. Z definicji sprzężenia magnetycznego obu cewek przy założonym zwrocie prądów i przyjęciu początków uzwojeń jak na rysunku wynikają następujące równania opisujące obwód | ||
: <math>U_1=jX_l_1I_1+jX_MI_2</math> | |||
: <math>U_2=-[jX_L_2I_2+jX_MI_1]</math> | |||
<math>U_2=-[jX_L_2I_2+jX_MI_1]</math> | |||
Znak minus występujący we wzorze na <math>U_2\,</math> wynika z kierunku <math>U_2\,</math> zaznaczonego na rysunku. Z równań wynika następujący wzór określający napięcie wyjściowe | Znak minus występujący we wzorze na <math>U_2\,</math> wynika z kierunku <math>U_2\,</math> zaznaczonego na rysunku. Z równań wynika następujący wzór określający napięcie wyjściowe | ||
: <math>U_2=-[\frac{X_M}{X_{L1}}U_1+jI_2(\frac{X_{L1}X_{L2}-X_M^2}{X_{L1}})]</math> | |||
<math>U_2=-[\frac{X_M}{X_{L1}}U_1+jI_2(\frac{X_{L1}X_{L2}-X_M^2}{X_{L1}})]</math> | |||
Przy założeniu wyidealizowanego transformatora <math>(k\approx 1 )</math> zachodzi <math>X_M^2\approx X_{L1}X_{L2}</math> . Oznacza to, że niezależnie od obciążenia relacja między napięciem pierwotnym i wtórnym dana jest w postaci | Przy założeniu wyidealizowanego transformatora <math>(k\approx 1 )</math> zachodzi <math>X_M^2\approx X_{L1}X_{L2}</math> . Oznacza to, że niezależnie od obciążenia relacja między napięciem pierwotnym i wtórnym dana jest w postaci | ||
: <math>U_2\approx -\frac{X_M}{X_{L1}}U_1</math> | |||
<math>U_2\approx -\frac{X_M}{X_{L1}}U_1</math> | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd22.png]] | ||
|valign="top"|Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji <math>X_{L1}=Kz_1^2, X_{L2}=Kz_2^2, X_M=Kz_1z_2</math> | |valign="top"|Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji <math>X_{L1}=Kz_1^2, X_{L2}=Kz_2^2, X_M=Kz_1z_2</math> gdzie <math>K</math> oznacza pewną stałą konstrukcyjną, to z zależności wynika | ||
<math>\frac{U_2}{U_1}=-\frac{z_2}{z_1}=-\frac{1}{n}</math> | : <math>\frac{U_2}{U_1}=-\frac{z_2}{z_1}=-\frac{1}{n}</math> | ||
Znak minus nie odgrywa żadnej roli a jedynie oznacza przesunięcie fazowe <math>180^o\,</math> napięcia wyjściowego względem wejściowego. Napięcie wtórne transformatora jest zależne wyłącznie od przekładni zwojowej i napięcia wejściowego układu. Jest to zatem realizacja podstawowej zależności charakterystycznej dla transformatora idealnego. Przy pominięciu strat w transformatorze moc na wejściu równa się mocy wyjściowej, stąd relacja między prądem pierwotnym i wtórnym spełnia również drugą zależność transformatora idealnego ). Wynika stąd wniosek, że transformator z rdzeniem ferromagnetycznym jest dobrym przybliżeniem transformatora idealnego. | Znak minus nie odgrywa żadnej roli a jedynie oznacza przesunięcie fazowe <math>180^o\,</math> napięcia wyjściowego względem wejściowego. Napięcie wtórne transformatora jest zależne wyłącznie od przekładni zwojowej i napięcia wejściowego układu. Jest to zatem realizacja podstawowej zależności charakterystycznej dla transformatora idealnego. Przy pominięciu strat w transformatorze moc na wejściu równa się mocy wyjściowej, stąd relacja między prądem pierwotnym i wtórnym spełnia również drugą zależność transformatora idealnego ). Wynika stąd wniosek, że transformator z rdzeniem ferromagnetycznym jest dobrym przybliżeniem transformatora idealnego. | ||
| Linia 329: | Linia 320: | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd23.png]] | ||
|valign="top"|Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej <math>n=2\,</math>. Przyjmiemy następujące wartości parametrów obwodu: <math>e(t)=10\sqrt2sin(\omega t)V, \omega=1rad/s, R=5\Omega, C=0,2F</math>. | |valign="top"|Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej <math>n=2\,</math>. Przyjmiemy następujące wartości parametrów obwodu: <math>e(t)=10\sqrt2sin(\omega t)V</math>, <math>\omega=1rad/s</math>, <math>R=5\Omega</math>, <math>C=0,2F</math>. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 344: | Linia 332: | ||
|valign="top"|Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami | |valign="top"|Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami | ||
<math>E=10</math> | : <math>E=10</math> | ||
<math>Z_C=-\frac{j}{\omega C}=-j5</math> | : <math>Z_C=-\frac{j}{\omega C}=-j5</math> | ||
<math>Z_R_C=\frac{RZ_C}{R_Z_C}=2,5-j2,5</math> | : <math>Z_R_C=\frac{RZ_C}{R_Z_C}=2,5-j2,5</math> | ||
Układ równań opisujących obwód wynika z praw Kirchhoffa i równań transformatora idealnego | Układ równań opisujących obwód wynika z praw Kirchhoffa i równań transformatora idealnego | ||
<math>E=RI_1+U_1</math> | : <math>E=RI_1+U_1</math> | ||
<math>U_1=nU_2</math> | : <math>U_1=nU_2</math> | ||
<math>I_1=\frac{1}{n}I_2</math> | : <math>I_1=\frac{1}{n}I_2</math> | ||
<math>U_2=I_2Z_{RC}</math> | : <math>U_2=I_2Z_{RC}</math> | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 369: | Linia 356: | ||
|valign="top"|Po wstawieniu wartości liczbowych otrzymuje się | |valign="top"|Po wstawieniu wartości liczbowych otrzymuje się | ||
<math>10=5I_1+U_1</math> | : <math>10=5I_1+U_1</math> | ||
<math>U_1=2U_2</math> | : <math>U_1=2U_2</math> | ||
<math>I_1=\frac{1}{2}I_2</math> | : <math>I_1=\frac{1}{2}I_2</math> | ||
<math>U_2=I_2(2,5-j2,5)</math> | : <math>U_2=I_2(2,5-j2,5)</math> | ||
Po uproszczeniu tego układu równań otrzymuje się | Po uproszczeniu tego układu równań otrzymuje się | ||
<math>10=(5+10\sqrt 2e^{-j45^o})I_1</math> | : <math>10=(5+10\sqrt 2e^{-j45^o})I_1</math> | ||
Stąd | Stąd | ||
<math>I_1=0,45+j0,30</math> | : <math>I_1=0,45+j0,30</math> | ||
<math>I_2=2I_1=0,90+j0,60</math> | : <math>I_2=2I_1=0,90+j0,60</math> | ||
<math>U_2=Z_{RC}I_2=3,79-j0,75</math> | : <math>U_2=Z_{RC}I_2=3,79-j0,75</math> | ||
<math>U_1=2U_2=758-j1,5</math> | : <math>U_1=2U_2=758-j1,5</math> | ||
<math>I_3=\frac{U_2}{R}=0,75-j0,15</math> | : <math>I_3=\frac{U_2}{R}=0,75-j0,15</math> | ||
<math>I_4=\frac{U_2}{Z_C}=0,15+j0,76</math> | : <math>I_4=\frac{U_2}{Z_C}=0,15+j0,76</math> | ||
Łatwo sprawdzić, że stosunek prądu <math>I_1\,</math> do prądu <math>I_2, \frac{I_1}{I_2}=\frac{1}{2}</math> podczas gdy <math>\frac{U_1}{U_2}=2</math> | Łatwo sprawdzić, że stosunek prądu <math>I_1\,</math> do prądu <math>I_2, \frac{I_1}{I_2}=\frac{1}{2}</math> podczas gdy <math>\frac{U_1}{U_2}=2</math> | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Wersja z 12:05, 31 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
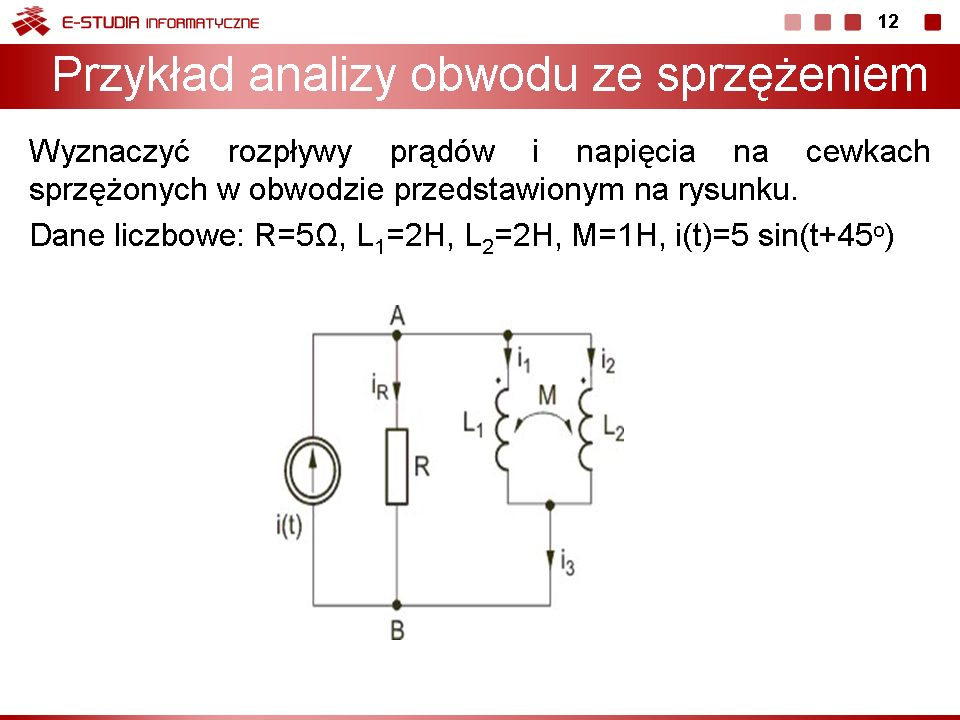
Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym.
Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. |

|
Rozwiązanie obwodu przebiega w następującej kolejności.
Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu:
|

|
Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej . Przyjmiemy następujące wartości parametrów obwodu: , , , . |

|
Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami
|

|
Po wstawieniu wartości liczbowych otrzymuje się
|