PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 88: | Linia 88: | ||
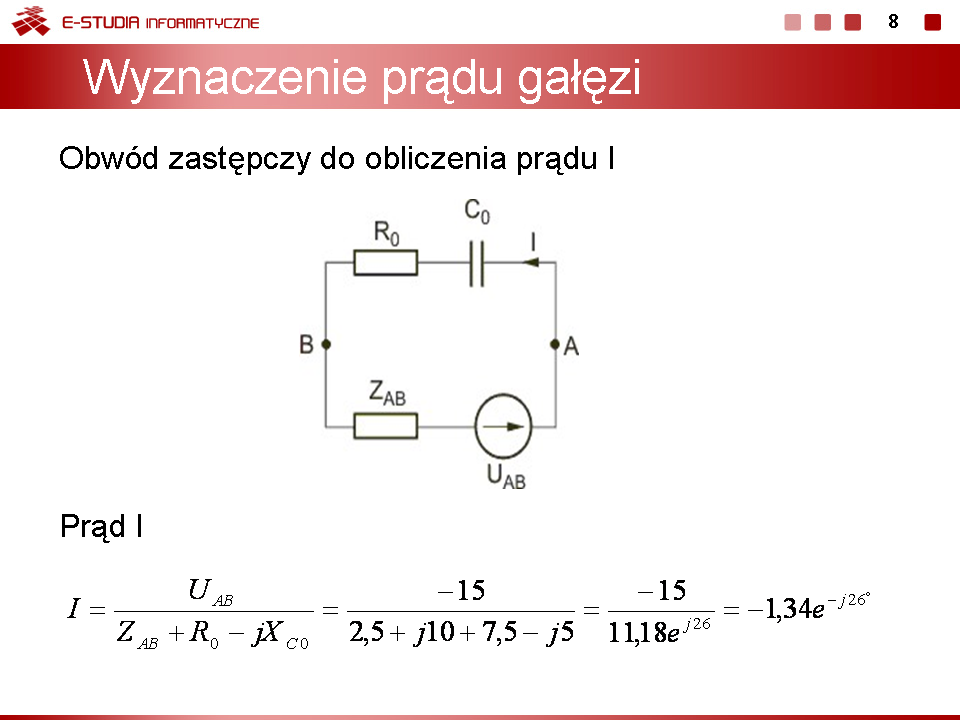
: <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | : <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | ||
Wartości chwilowe prądu <math>i(t)\,</math> wyznaczane są z zależności | Wartości chwilowe prądu <math>i(t)\,</math> wyznaczane są z zależności | ||
| Linia 159: | Linia 160: | ||
|valign="top"|Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci | |valign="top"|Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci | ||
<math>\mathbf{YV}=\mathbf{I}_{zr}</math> | : <math>\mathbf{YV}=\mathbf{I}_{zr}</math> | ||
<math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | : <math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | ||
w której <math>\mathbf{Y}</math>, jest macierzą węzłową o wymiarach <math>NxN\,</math>, gdzie <math>N\,</math> jest liczbą węzłów niezależnych w obwodzie, <math>\mathbf{V}\,</math> jest wektorem niezależnych potencjałów węzłowych o wymiarze <math>N\,</math> a <math>\mathbf{I}_{zr}</math> jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa <math>\mathbf{Y}</math>, określona jest w postaci | w której <math>\mathbf{Y}</math>, jest macierzą węzłową o wymiarach <math>NxN\,</math>, gdzie <math>N\,</math> jest liczbą węzłów niezależnych w obwodzie, <math>\mathbf{V}\,</math> jest wektorem niezależnych potencjałów węzłowych o wymiarze <math>N\,</math> a <math>\mathbf{I}_{zr}</math> jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa <math>\mathbf{Y}</math>, określona jest w postaci | ||
<math>\mathbf{Y}=\begin{bmatrix} | : <math>\mathbf{Y}=\begin{bmatrix} | ||
Y_{11} & Y_{12} & \cdots & Y_{1N} \\ | Y_{11} & Y_{12} & \cdots & Y_{1N} \\ | ||
Y_{21} & Y_{22} & \cdots & Y_{2N} \\ | Y_{21} & Y_{22} & \cdots & Y_{2N} \\ | ||
| Linia 177: | Linia 178: | ||
<math>\mathbf{V}=\begin{bmatrix} | : <math>\mathbf{V}=\begin{bmatrix} | ||
V_1 \\ | V_1 \\ | ||
V_2 \\ | V_2 \\ | ||
Wersja z 11:56, 31 sie 2006

|
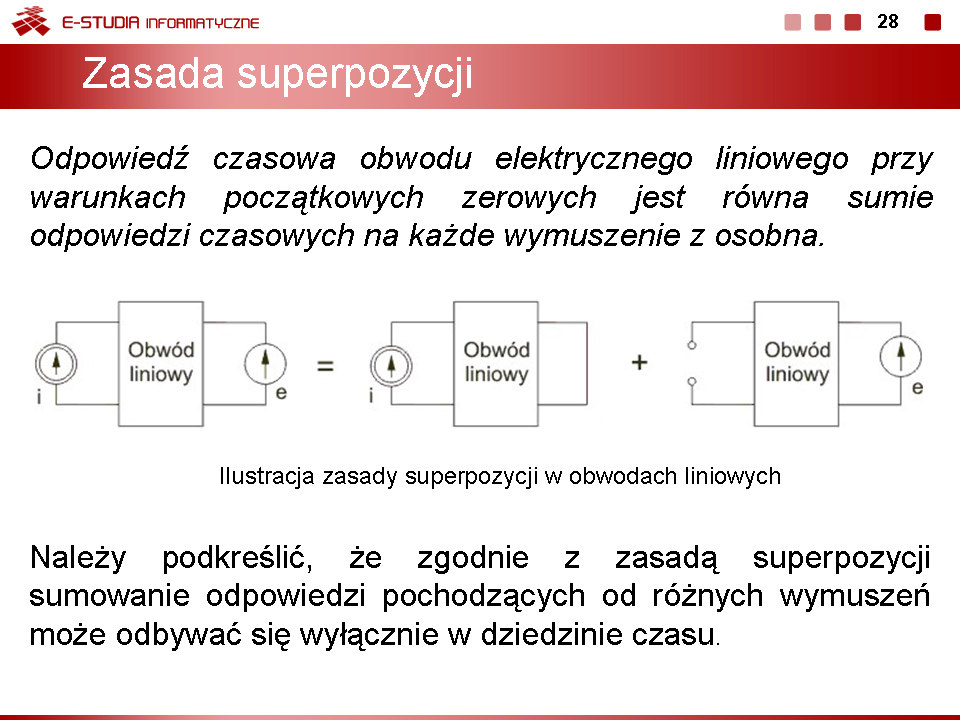
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |

|
Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie
|
| Zadania sprawdzające
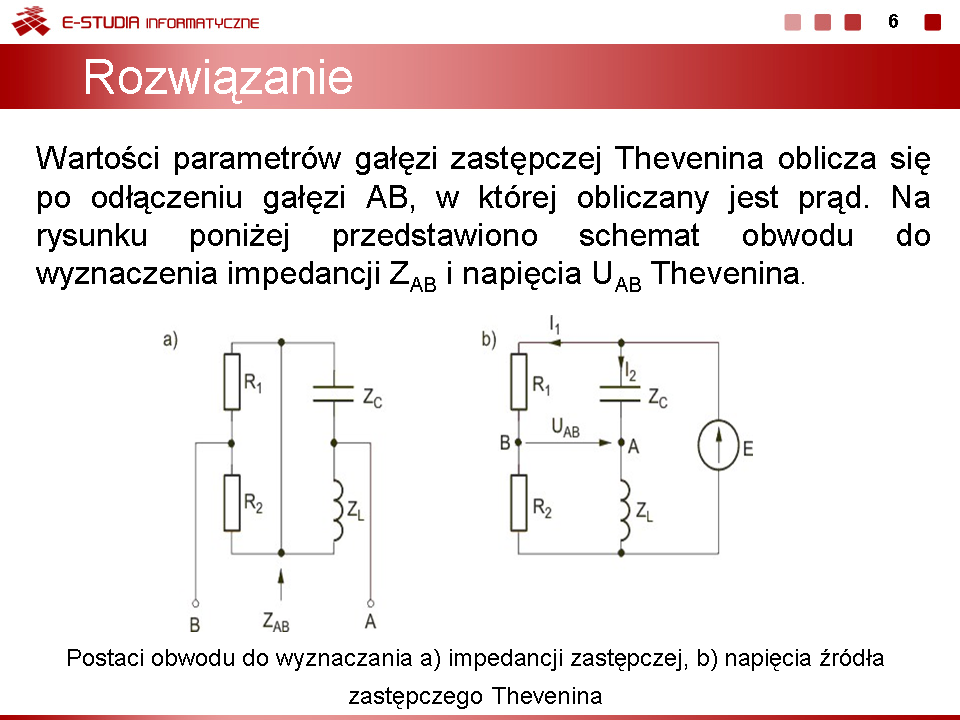
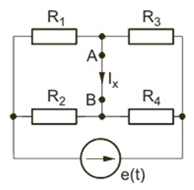
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , .
Impedancja z zacisków AB obwodu (rysunek a) jest równa
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
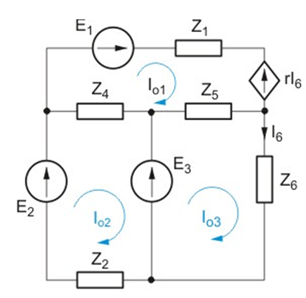
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci
|