MN01LAB: Różnice pomiędzy wersjami
mNie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
= | <!-- | ||
Konwertowane z pliku LaTeX przez latex2mediawiki, zob. http://www.ii.uj.edu.pl/ pawlik1/latex2mediawiki.php | |||
--> | |||
=Ćwiczenia. Eksperymenty ze środowiskiem obliczeń numerycznych= | |||
W Linuxie, czas działania programu można zbadać poleceniem <code>time</code>. | W Linuxie, czas działania programu można zbadać poleceniem <code>time</code>. | ||
| Linia 11: | Linia 15: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
x | x = 1.0; | ||
for( i | for( i = 0; i < N; i++) | ||
x | x = x/3.0; | ||
</pre></div> | </pre></div> | ||
| Linia 19: | Linia 23: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
x | x = 1.0; f = 1.0/3.0; | ||
for( i | for( i = 0; i < N; i++) | ||
x | x = x*f; | ||
</pre></div> | </pre></div> | ||
| Linia 32: | Linia 36: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
x | x = 1.0; | ||
for( i | for( i = 0; i < N; i++) | ||
x | x = x*(1.0/3.0); | ||
</pre></div> | </pre></div> | ||
| Linia 54: | Linia 58: | ||
* binarnego | * binarnego | ||
kolejne wartości <math>\displaystyle \sin(\pi | kolejne wartości <math>\displaystyle \sin(\pi\cdot i\cdot 0.4)</math>, gdzie <math>\displaystyle i=0,\ldots, 1024</math>. Następnie porównaj | ||
rozmiary plików i możliwości ich odczytania zewnętrznymi narzędziami. Wreszcie, | rozmiary plików i możliwości ich odczytania zewnętrznymi narzędziami. Wreszcie, | ||
wczytaj liczby z pliku i porównaj je z oryginalnymi wartościami sinusa. Czy | wczytaj liczby z pliku i porównaj je z oryginalnymi wartościami sinusa. Czy | ||
| Linia 74: | Linia 78: | ||
Pomyśl, jak obliczać, korzystając jedynie z czterech działań podstawowych: <math>\displaystyle +,\, | Pomyśl, jak obliczać, korzystając jedynie z czterech działań podstawowych: <math>\displaystyle +,\, | ||
-, \, \times, \, \div</math>, wartość funkcji <code>exp(</code><math>\displaystyle x</math><code>)</code | -, \, \times, \, \div</math>, wartość funkcji <code>exp(</code><math>\displaystyle x</math><code>)</code> = <math>\displaystyle e^x</math> dla | ||
dowolnych <math>\displaystyle x</math> rzeczywistych. Naszym kryterium jest, by <math>\displaystyle |e^x - \exp(x)| \leq | dowolnych <math>\displaystyle x</math> rzeczywistych. Naszym kryterium jest, by <math>\displaystyle |e^x - \exp(x)| \leq | ||
\epsilon</math>, czyli by błąd bezwzględny aproksymacji nie przekroczył zadanego | \epsilon</math>, czyli by błąd bezwzględny aproksymacji nie przekroczył zadanego | ||
| Linia 133: | Linia 137: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
function [y, N] | function [y, N] = expa(x, epsilon) | ||
y | y = skladnik = 1.0; N = 1; | ||
while (abs(skladnik) > epsilon) | while (abs(skladnik) > epsilon) | ||
skladnik * | skladnik *= (x/N); | ||
y + | y += skladnik; | ||
N++; | N++; | ||
end | end | ||
| Linia 148: | Linia 152: | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
function [blad, relblad, koszt] | function [blad, relblad, koszt] = testexp(expX, x) | ||
dokladnie | dokladnie = exp(x); | ||
[wartosc, koszt] | [wartosc, koszt] = feval(expX,x,1e-8); | ||
blad | blad = abs(wartosc-dokladnie); | ||
relblad | relblad = blad/dokladnie; | ||
end | end | ||
i | i = 0; zakres = linspace(0,7,100); | ||
for x | for x = zakres | ||
fprintf(stderr,'x | fprintf(stderr,'x = %e\n', x); | ||
[blad, relblad, koszt] | i++; | ||
koszta(i) | [blad, relblad, koszt] = testexp('expa',x); | ||
blada(i) | koszta(i) = koszt; relblada(i) = relblad; | ||
blada(i) = blad; | |||
end | end | ||
xlabel('x'); | xlabel('x'); | ||
ylabel('blad'); | ylabel('blad'); | ||
title(['Epsilon | title(['Epsilon = ', num2str(epsilon)]); | ||
plot(zakres, relblada, ';blad wzgledny;'); | plot(zakres, relblada, ';blad wzgledny;'); | ||
plot(zakres, blada, ';blad bezwzgledny;'); | plot(zakres, blada, ';blad bezwzgledny;'); | ||
| Linia 172: | Linia 177: | ||
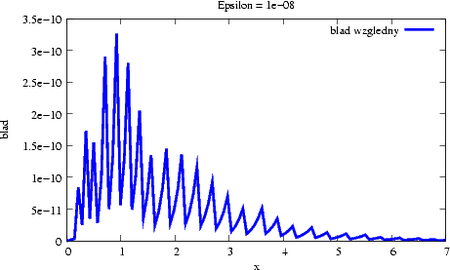
Zgodnie z oczekiwaniami, błąd jest poniżej zadanej tolerancji, tutaj: <math>\displaystyle 10^{-8}</math>. | Zgodnie z oczekiwaniami, błąd jest poniżej zadanej tolerancji, tutaj: <math>\displaystyle 10^{-8}</math>. | ||
[[Image:MNbladwzglednyexpa.png|thumb| | [[Image:MNbladwzglednyexpa.png|thumb|450px|center|Błąd względny aproksymacji wielomianem Taylora.]] | ||
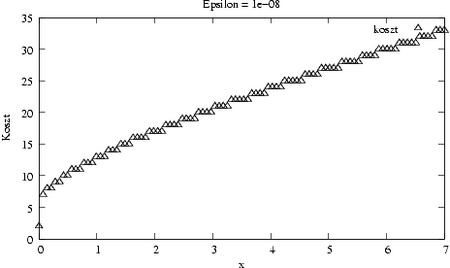
Jednak koszt aproksymacji rośnie wraz z <math>\displaystyle x</math>: | Jednak koszt aproksymacji rośnie wraz z <math>\displaystyle x</math>: | ||
[[Image:MNkosztexpa.png|thumb| | [[Image:MNkosztexpa.png|thumb|450px|center|Koszt aproksymacji wielomianem Taylora.]] | ||
Niektóre wyniki mogą Cię jednak zaskoczyć: | Niektóre wyniki mogą Cię jednak zaskoczyć: | ||
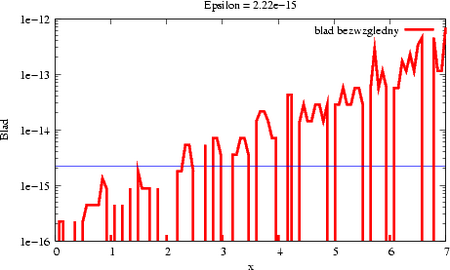
* Błąd bezwzględny przekracza założoną wartość, gdy <math>\displaystyle \epsilon = 2.2\cdot | * Błąd bezwzględny przekracza założoną wartość, gdy <math>\displaystyle \epsilon = 2.2\cdot | ||
10^{-15}</math>, a błąd względny od pewnego momentu | 10^{-15}</math>, a błąd względny od pewnego momentu <strong>rośnie</strong> z <math>\displaystyle x</math>. | ||
[[Image:MNbladbezwzglednyexpaeps.png|thumb| | [[Image:MNbladbezwzglednyexpaeps.png|thumb|450px|center|Błąd względny aproksymacji wielomianem Taylora dla zadanej bardzo małej | ||
tolerancji błędu.]] | tolerancji błędu.]] | ||
* Nie daje się tak policzyć <math>\displaystyle e^{2006}</math>. | * Nie daje się tak policzyć <math>\displaystyle e^{2006}</math>. | ||
| Linia 187: | Linia 192: | ||
Wyjaśnienie tych szokujących faktów (które nie mają nic wspólnego z błędem w | Wyjaśnienie tych szokujących faktów (które nie mają nic wspólnego z błędem w | ||
implementacji) musisz odłożyć do momentu, gdy bliżej przyjrzymy się temu, | implementacji) musisz odłożyć do momentu, gdy bliżej przyjrzymy się temu, <strong>jak</strong> | ||
liczy komputer. | liczy komputer. | ||
| Linia 214: | Linia 219: | ||
</math></center> | </math></center> | ||
Tak więc zadanie redukuje się do wyznaczenia <math>\displaystyle \exp(t)</math> dla | Tak więc zadanie redukuje się do wyznaczenia <math>\displaystyle \exp(t)</math> dla <strong>małego</strong> <math>\displaystyle t</math> oraz | ||
do co najwyżej <math>\displaystyle k</math> dodatkowych mnożeń potrzebnych do wyznaczenia całkowitej | do co najwyżej <math>\displaystyle k</math> dodatkowych mnożeń potrzebnych do wyznaczenia całkowitej | ||
potęgi <math>\displaystyle e^k</math> (ile mnożeń | potęgi <math>\displaystyle e^k</math> (ile mnożeń <strong>naprawdę</strong> wystarczy?). Pamiętaj, przyjęliśmy, że | ||
znamy reprezentację numeryczną liczby <math>\displaystyle e</math>. | znamy reprezentację numeryczną liczby <math>\displaystyle e</math>. | ||
<div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | <div class="code" style="background-color:#e8e8e8; padding:1em"><pre> | ||
[Wersja B] | [Wersja B] | ||
function [y, N] | function [y, N] = expb(x, epsilon) | ||
k | k = floor(x); t = x - k; | ||
[y, N] | [y, N] = expa(t, epsilon); | ||
for i | for i = 1:k | ||
y * | y *= e; | ||
end | end | ||
N + | N += (k+2); | ||
end | end | ||
</pre></div> | </pre></div> | ||
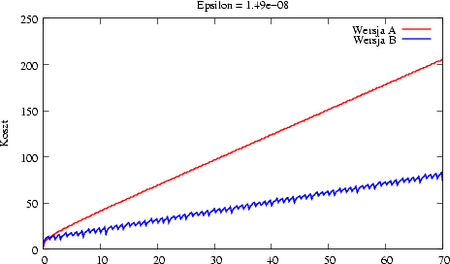
[[Image:MNkosztexpab.png|thumb| | [[Image:MNkosztexpab.png|thumb|450px|center|Wersja B jest istotnie tańsza.]] | ||
</div></div></div> | </div></div></div> | ||
Wersja z 16:44, 2 wrz 2006
Ćwiczenia. Eksperymenty ze środowiskiem obliczeń numerycznych
W Linuxie, czas działania programu można zbadać poleceniem time.
Ćwiczenie
Który program wykona się szybciej:
x = 1.0; for( i = 0; i < N; i++) x = x/3.0;
czy
x = 1.0; f = 1.0/3.0; for( i = 0; i < N; i++) x = x*f;
Ćwiczenie
Napisz program w C, który zapisuje do pliku
- tekstowego
- binarnego
kolejne wartości , gdzie . Następnie porównaj rozmiary plików i możliwości ich odczytania zewnętrznymi narzędziami. Wreszcie, wczytaj liczby z pliku i porównaj je z oryginalnymi wartościami sinusa. Czy możesz wyjaśnić przyczyny różnic?
Powtórz to samo w Octave.
Ćwiczenie: Implementacja funkcji matematycznych
Pomyśl, jak obliczać, korzystając jedynie z czterech działań podstawowych: , wartość funkcji exp() = dla
dowolnych rzeczywistych. Naszym kryterium jest, by , czyli by błąd bezwzględny aproksymacji nie przekroczył zadanego
.
Wykonaj eksperymenty w C lub w Octave, pokazujące koszt metody w zależności od
oraz w zależności od . Przeprowadź też sekwencję testów
potwierdzających Twoje rachunki co do oczekiwanej dokładności (porównując się z
funkcją biblioteczną). W C możesz korzystać ze stałej M_E , zdefiniowanej w pliku nagłówkowym math.h.
Ćwiczenie: Ciag dalszy
Spróbuj obniżyć koszt wyznaczania dla dużych !