MN01LAB: Różnice pomiędzy wersjami
mNie podano opisu zmian |
|||
| Linia 1: | Linia 1: | ||
==Eksperymenty ze środowiskiem obliczeń numerycznych== | |||
== | |||
W Linuxie, czas działania programu można zbadać poleceniem \lstux!time!. | W Linuxie, czas działania programu można zbadać poleceniem \lstux!time!. | ||
| Linia 233: | Linia 232: | ||
</pre></div> | </pre></div> | ||
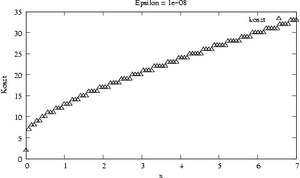
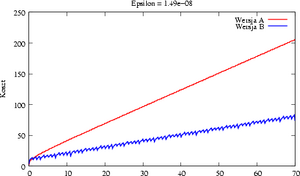
[[Image:MNkosztexpab.png|thumb|300px|Wersja B]] | [[Image:MNkosztexpab.png|thumb|300px|Wersja B, w której sprytnie redukujemy zadanie do | ||
wyznaczania <math>e^t</math> dla <math>t\in [0,1]</math> jest istotnie tańsza.]] | |||
</div></div></div> | </div></div></div> | ||
Wersja z 14:11, 29 sie 2006
Eksperymenty ze środowiskiem obliczeń numerycznych
W Linuxie, czas działania programu można zbadać poleceniem \lstux!time!.
Ćwiczenie
Który program wykona się szybciej:
x = 1.0; for( i = 0; i < N; i++) x = x/3.0;
czy
x = 1.0; f = 1.0/3.0; for( i = 0; i < N; i++) x = x*f;
Ćwiczenie
Napisz program w C, który zapisuje do pliku
- tekstowego
- binarnego
kolejne wartości , gdzie . Następnie porównaj rozmiary plików i możliwości ich odczytania zewnętrznymi narzędziami. Wreszcie, wczytaj liczby z pliku i porównaj je z oryginalnymi wartościami sinusa. Czy możesz wyjaśnić przyczyny różnic?
Powtórz to samo w Octave.
Ćwiczenie: Implementacja funkcji matematycznych
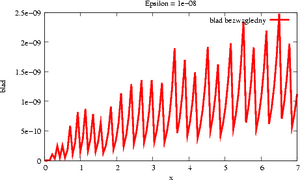
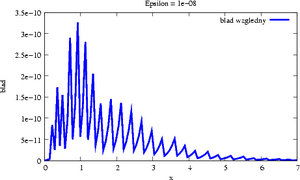
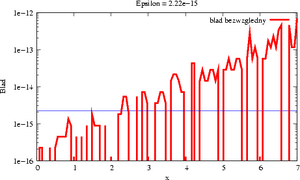
Pomyśl, jak obliczać, korzystając jedynie z czterech działań podstawowych: , wartość funkcji exp() = dla
dowolnych rzeczywistych. Naszym kryterium jest, by , czyli by błąd bezwzględny aproksymacji nie przekroczył zadanego
.
Wykonaj eksperymenty w C lub w Octave, pokazujące koszt metody w zależności od
oraz w zależności od . Przeprowadź też sekwencję testów
potwierdzających Twoje rachunki co do oczekiwanej dokładności (porównując się z
funkcją biblioteczną). W C możesz korzystać ze stałej M_E , zdefiniowanej w pliku nagłówkowym \lstux!math.h!.
Ćwiczenie: Ciag dalszy
Spróbuj obniżyć koszt wyznaczania dla dużych !