Laboratorium wirtualne 2/Moduł 2 - ćwiczenie 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
|||
| Linia 9: | Linia 9: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd_intro.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd_intro.png]] | ||
|valign="top"| | |valign="top"|'''Temat ćwiczenia:''' | ||
System pomiarowy do wyznaczania podstawowych parametrów i charakterystyk czwórników | |||
'''Cel ćwiczenia:''' | |||
Celem ćwiczenia jest zapoznanie się i pomiar podstawowych parametrów i charakterystyk wybranych czwórników aktywnych. Ćwiczenie składa się z dwóch elementów: | |||
*Pomiar podstawowych parametrów akustycznego wzmacniacza mocy. | |||
*Wyznaczenie charakterystyk amplitudowych i fazowych filtrów aktywnych. | |||
|} | |} | ||
| Linia 22: | Linia 31: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd02.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd02.png]] | ||
|valign="top"| | |valign="top"|Celem ćwiczenia jest zapoznanie się z charakterystykami częstotliwościowymi podstawowych członów dynamicznych. W trakcie ćwiczenia uczestnik pozna sposoby wyznaczania podstawowych charakterystyk częstotliwościowych układów dynamicznych oraz podstawowe parametry wzmacniacza mocy (w ćwiczeniu użyty został wzmacniacz akustyczny) i sposoby ich wyznaczania. W trakcie ćwiczenia uczestnik nabędzie podstawowe informacje dotyczące charakterystyk częstotliwościowych i transmitancji układu oraz związku pomiędzy nimi. | ||
|} | |} | ||
| Linia 29: | Linia 38: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd03.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd03.png]] | ||
|valign="top"| | |valign="top"|Plan i przebieg ćwiczenia. | ||
|} | |} | ||
| Linia 36: | Linia 45: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd04.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd04.png]] | ||
|valign="top"| | |valign="top"|Podstawy teoretyczne podzielone zostały na następujące części; | ||
*Podstawowe człony dynamiczne | |||
*Podstawowe charakterystyki czasowe | |||
**charakterystyka skokowa | |||
**charakterystyka impulsowa | |||
**charakterystyka liniowo-czasowa | |||
*Charakterystyki częstotliwościowe układów dynamicznych | |||
**Związki charakterystyk częstotliwościowych z transmitancją układu | |||
**Charakterystyka amplitudowa | |||
**Charakterystyka fazowa | |||
**Sposoby wykreślania charakterystyk częstotliwościowych | |||
*Wzmacniacze mocy | |||
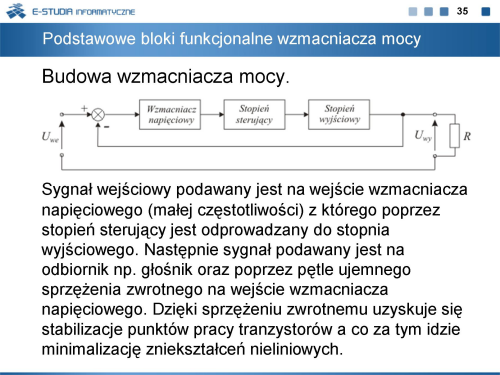
**Podstawowe bloki funkcjonalne wzmacniacza mocy | |||
**Klasy pracy wzmacniaczy | |||
**Podstawowe parametry wzmacniacza mocy | |||
|} | |} | ||
| Linia 43: | Linia 66: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="450px"|[[Grafika:LW2_M2_Slajd05.png]] | |valign="top" width="450px"|[[Grafika:LW2_M2_Slajd05.png]] | ||
|valign="top"| | |valign="top"|Ćwiczenie podzielone zostało na dwie części. Pierwszą z nich jest poznanie sposobu wyznaczania charakterystyk częstotliwościowych układów aktywnych. W zależności od osoby prowadzącej ćwiczenie analizie może być podany prosty filtr aktywny oparty o wzmacniacz operacyjny lub pasywny filtr RC. W ćwiczeniu wyznacza się charakterystyki częstotliwościowe badanego filtru oraz podejmuje się próbę identyfikacji układu i wyznaczenia jego transmitancji. Na podstawie wyznaczonej transmitancji układu wykonuje się symulację i wyznaczenie charakterystyk częstotliwościowych w środowisku Matlab. | ||
Drugą częścią ćwiczenia jest wyznaczenie podstawowych charakterystyk i parametrów akustycznego wzmacniacza mocy. | |||
|} | |} | ||
| Linia 50: | Linia 76: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd06.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd06.png]] | ||
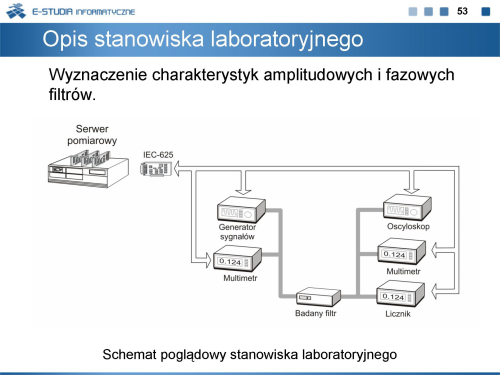
|valign="top"| | |valign="top"|Szczegółowy plan części pierwszej ćwiczenia polegającej na wyznaczenie charakterystyk amplitudowych i fazowych filtrów. | ||
|} | |} | ||
| Linia 56: | Linia 82: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd07.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd07.png]] | ||
|valign="top"| | |valign="top"|Szczegółowy plan części drugiej ćwiczenia polegającego na pomiarze podstawowych parametrów akustycznego wzmacniacza mocy. | ||
|} | |} | ||
| Linia 63: | Linia 89: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd08.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd08.png]] | ||
|valign="top"| | |valign="top"|Jedną z podstawowych metod określania właściwości układów dynamicznych jest wyznaczanie ich charakterystyk czasowych i częstotliwościowych opisujących związek pomiędzy odpowiedzią układu a zadanym wymuszeniem. W przypadku charakterystyk częstotliwościowych stosuje się wymuszenie harmoniczne zmieniające się w zadanym przedziale częstotliwości. | ||
|} | |} | ||
| Linia 76: | Linia 102: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd10.png]] | ||
|valign="top"| | |valign="top"|Członem układu nazywa się urządzenie lub układ o wyodrębnionym wejściu i wyjściu będący częścią składową tego układu. W ćwiczeniu zajmujemy się czwórnikami (układami) dynamicznymi aniżeli układami automatyki. Istnieje ograniczona liczba liniowych członów podstawowych o jednym wejściu i jednym wyjściu oraz o prostych charakterystykach. Złożone liniowe układy dynamiczne można przedstawić jako ich połączenia. Schemat przedstawiający te połączenia nazywa się schematem strukturalnym (blokowym) układu złożonego. | ||
|} | |} | ||
| Linia 82: | Linia 108: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd11.png]] | ||
|valign="top"| | |valign="top"|Człon proporcjonalny (inaczej: bezinercyjny, wzmacniający) to człon, który na wyjściu daje sygnał y(t) proporcjonalny do sygnału wejściowego x(t). | ||
Na slajdzie został przedstawiony przykład członu proporcjonalnego oraz jego transmitancja. | |||
|} | |} | ||
| Linia 89: | Linia 118: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd12.png]] | ||
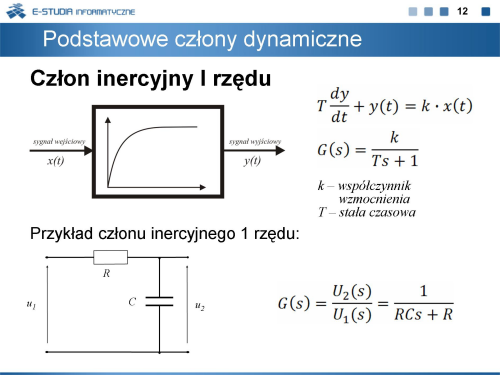
|valign="top"| | |valign="top"|Na slajdzie został przedstawiony przykład członu inercyjnego 1 rzędu oraz jego transmitancja. | ||
|} | |} | ||
| Linia 96: | Linia 125: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd13.png]] | ||
|valign="top"| | |valign="top"|Człon całkujący (idealny) to człon, który na wyjściu daje sygnał y(t) proporcjonalny do całki sygnału wejściowego x(t). Na slajdzie został przedstawiony przykład członu całkującego oraz jego transmitancja. | ||
|} | |} | ||
| Linia 103: | Linia 132: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd14.png]] | ||
|valign="top"| | |valign="top"|Człon różniczkujący (idealny) to człon, który na wyjściu daje sygnał y(t) proporcjonalny do pochodnej sygnału wejściowego x(t). Na slajdzie został przedstawiony przykład członu różniczkującego oraz jego transmitancja. | ||
|} | |} | ||
| Linia 110: | Linia 139: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="450px"|[[Grafika:LW2_M2_Slajd15.png]] | |valign="top" width="450px"|[[Grafika:LW2_M2_Slajd15.png]] | ||
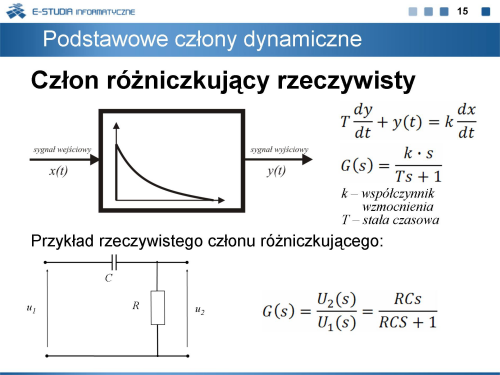
|valign="top"| | |valign="top"|Na slajdzie został przedstawiony przykład członu rzeczywistego różniczkującego oraz jego transmitancja. | ||
|} | |} | ||
| Linia 123: | Linia 152: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd17.png]] | ||
|valign="top"| | |valign="top"|Charakterystyki czasowe służą do opisywania i porównywania właściwości dynamicznych układów a do ich wyznaczania używa się tych samych zestandaryzowanych sygnałów testowych. Charakterystyką czasową układu nazywamy przebieg w czasie odpowiedzi układu na określony sygnał wejściowy podany na wejście układu będącego w stanie równowagi (w którym nie zachodzą żadne procesy przejściowe). | ||
|} | |} | ||
| Linia 130: | Linia 159: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd18.png]] | ||
|valign="top"| | |valign="top"|W zależności od zastosowanego sygnału wejściowego można wyróżnić następujące charakterystyki czasowe: | ||
*charakterystyka skokowa | |||
*charakterystyka impulsowa | |||
*charakterystyka liniowo-czasowa | |||
|} | |} | ||
| Linia 136: | Linia 170: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd19.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd19.png]] | ||
|valign="top"| | |valign="top"|Charakterystyka skokowa jest odpowiedzią układu h(t) na którego wejście podano sygnał skokowy przy zerowych warunkach początkowych. | ||
|} | |} | ||
| Linia 143: | Linia 177: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd20.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd20.png]] | ||
|valign="top"| | |valign="top"|Charakterystyka impulsowa jest odpowiedzią układu na którego wejście podano sygnał w postaci impulsu Diraca. Znajomość odpowiedzi impulsowej pozwala przewidzieć odpowiedź układu na każde inne pobudzenie. Odpowiedź układu na dowolne pobudzenie jest bowiem splotem sygnału pobudzającego oraz odpowiedzi impulsowej układu. | ||
W akustyce często wyznacza się odpowiedź impulsową pomieszczenia poprzez nagranie w nim krótkiego i silnego impulsu dźwiękowego. Pozwala to na przetwarzanie innych nagrań (splatanie ich z odpowiedzią impulsową pomieszczenia) i otrzymanie efektu dźwiękowego polegającego na symulacji nagrania w danym pomieszczeniu. Wykorzystywane jest to w przemyśle filmowy w czasie podkładania dialogu do całości nagrania. | |||
|} | |} | ||
| Linia 150: | Linia 187: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd21.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd21.png]] | ||
|valign="top"| | |valign="top"|Charakterystyka liniowo-czasowa jest odpowiedzią układu na wejście którego podano sygnał liniowo zależny od czasu. | ||
|} | |} | ||
| Linia 164: | Linia 201: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd23.png]] | ||
|valign="top"| | |valign="top"|Jedną z podstawowych metod określania właściwości układów dynamicznych jest wyznaczanie ich charakterystyk częstotliwościowych opisujących związek pomiędzy odpowiedzią układu a zadanym wymuszeniem harmonicznym zmieniającym się w zadanym przedziale częstotliwości. | ||
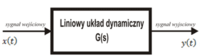
: [[Grafika:LW2_M2_CW2_rys.png|none|thumb|200px|Liniowy układ dynamiczny]] | |||
Jeżeli na wejście układu liniowego podane zostanie wymuszenie sinusoidalne o stałej pulsacji <math>\omega = 2\pi f [rad/s]</math> | |||
: <math>x(t)=X_msin(\omega t + \varphi_x)</math> | |||
to na wyjściu tego układu po zaniknięciu procesów przejściowych otrzymamy również odpowiedź sinusoidalną o tej samej pulsacji <math>\omega</math> w co sygnał wyjściowy | |||
: <math>y(t)=Y_msin(\omega t + \varphi_y)</math> | |||
|} | |} | ||
| Linia 171: | Linia 218: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd24.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd24.png]] | ||
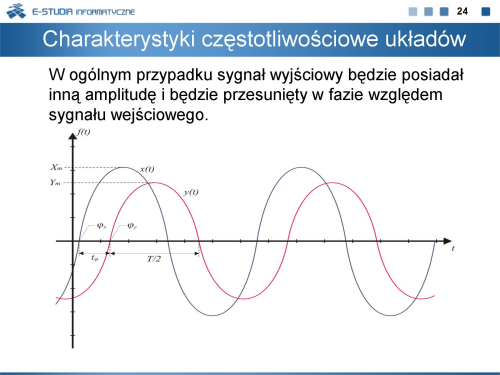
|valign="top"| | |valign="top"|W ogólnym przypadku sygnał wyjściowy będzie posiadał inną amplitudę i będzie przesunięty w fazie względem sygnału wejściowego. | ||
|} | |} | ||
| Linia 178: | Linia 225: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="450px"|[[Grafika:LW2_M2_Slajd25.png]] | |valign="top" width="450px"|[[Grafika:LW2_M2_Slajd25.png]] | ||
|valign="top"| | |valign="top"|Charakterystyki częstotliwościowe opisują zachowanie się układu dla wszystkich wielkości pulsacji w sygnału wejściowego. Jeżeli znany jest model matematyczny liniowego układu dynamicznego w postaci transmitancji operatorowej <math>G(s)</math> można wyznaczyć transmitancję widmową, która jest równa stosunkowi wartości zespolonej odpowiedzi układu, wywołanej wymuszeniem sinusoidalnym do wartości tego wymuszenia w stanie ustalonym. Przez transmitancję widmową rozumiemy: | ||
: <math>G(j\omega)=G(s)|_{s=j\omega}={Y(j\omega) \over X(j\omega)}</math> | |||
|} | |} | ||
| Linia 185: | Linia 235: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd26.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd26.png]] | ||
|valign="top"| | |valign="top"|Wykres <math>G(j\omega)</math> nazywa się charakterystyką amplitudowo-fazową. Reprezentuje on przestrzeń geometryczną końców wektorów, których długość reprezentuje stosunek amplitud odpowiedzi do wymuszenia, a kąt odpowiada przesunięciu fazowemu pomiędzy odpowiedzią a wymuszeniem. | ||
|} | |} | ||
| Linia 191: | Linia 241: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd27.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd27.png]] | ||
|valign="top"| | |valign="top"|Transmitancja widmowa jest funkcją zmiennej zespolonej, której koniec wektora <math>G(j\omega_1)</math> o długości <math>A(\omega_1)</math> i kącie nachylania do osi ox <math>\phi(j\omega_1)</math> wyznacza na płaszczyźnie zespolonej punkty o współrzędnych <math>P(\omega_1)</math> i <math>Q(\omega_1)</math>. Jeżeli pulsacja w ulega zmianie, wówczas wektor <math>G(j\omega)</math> zmienia swoją wartość bezwzględną i obraca się gdyż jego argument <math>\phi(j\omega_1)</math>, także zależy od pulsacji. Koniec wektora <math>G(j\omega)</math> opisze krzywą będącą charakterystyką amplitudowo-fazową (Nyquista). Charakterystyki amplitudowo-fazowe układów rzeczywistych, dla których stopień wielomianu licznika transmitancji jest niższy od stopnia wielomianu mianownika, dążą do początku układu współrzędnych. | ||
|} | |} | ||
| Linia 198: | Linia 248: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd28.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd28.png]] | ||
|valign="top"| | |valign="top"|W czasie wyznaczania charakterystyk częstotliwościowych układów dynamicznych jako sygnał testowy stosuje się najczęściej wymuszenie harmoniczne o częstotliwości zmieniającej się w określonym zakresie (teoretycznie zmiany częstotliwości powinny być w zakresie <math>0 \le \omega \le \infty</math>). Sygnał sinusoidalny stosuje się także do określania parametrów i jakości wzmacniaczy mocy (np. akustycznych). Zastosowanie sygnału sinusoidalnego jako sygnału testowego wynika z kilku powodów. Najważniejszy z nich mówi, że odpowiedź stabilnego, liniowego układu dla dowolnego sygnału okresowego jest sumą odpowiedzi dla każdej składowej (sinusoidalnej) sygnału wejściowego (rozkład sygnału na szereg Fouriera). Ponadto każdy sygnał okresowy można wyrazić jako sumę sygnałów sinusoidalnych, a te z kolei są łatwe do wygenerowania. | ||
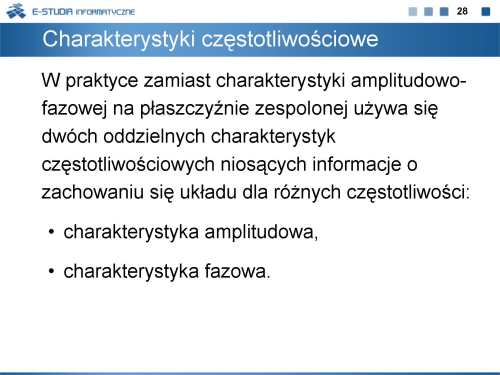
W praktyce zamiast charakterystyki amplitudowo-fazowej na płaszczyźnie zespolonej używa się dwóch oddzielnych charakterystyk częstotliwościowych niosących informacje o zachowaniu się układu dla różnych częstotliwości: | |||
*charakterystyka amplitudowa, | |||
*charakterystyka fazowa. | |||
|} | |} | ||
| Linia 204: | Linia 260: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd29.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd29.png]] | ||
|valign="top"| | |valign="top"|'''Charakterystyka amplitudowa''' <math>A(\omega)</math> jest to stosunek amplitudy sygnału wyjściowego do amplitudy sygnału wejściowego (wzmocnienie układu) w funkcji częstotliwości \omega. | ||
Przy zdejmowaniu charakterystyki częstotliwościowej amplituda sygnału wejściowego jest zwykle utrzymywana na stałym poziomie <math>X_m(\omega)=X_m=const</math>. | |||
|} | |} | ||
| Linia 211: | Linia 270: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd30.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd30.png]] | ||
|valign="top"| | |valign="top"|'''Charakterystyka fazowa''' <math>\varphi(\omega)</math> jest to przesunięcie fazowe (podawane w stopniach lub radianach) sygnału wyjściowego w stosunku do sygnału wejściowego w funkcji częstotliwości <math>\omega</math>: | ||
: <math>\varphi(\omega)=\varphi_x(\omega)-\varphi_y(\omega)</math> | |||
Jeżeli sygnał wyjściowy jest opóźniony w stosunku do wejściowego, to przesunięcie fazowe <math>\varphi(\omega)</math> ma wartość ujemną. | |||
|} | |} | ||
| Linia 217: | Linia 281: | ||
{| border="0" cellpadding="5" width="100%" | {| border="0" cellpadding="5" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW2_M2_Slajd31.png]] | |valign="top" width="500px"|[[Grafika:LW2_M2_Slajd31.png]] | ||
|valign="top"| | |valign="top"|Pierwszym sposobem wykreślania charakterystyk częstotliwościowych jest zaprezentowany wcześniej wykres <math>G(j\omega)</math> często nazywany hodografem wektora <math>G(j\omega)</math> na płaszczyźnie zespolonej (przedstawiony na Rysunek 1). Wykres często nazywany jest też wykresem Nyquista bądź charakterystyką widmową układu przedstawioną na płaszczyźnie zespolonej. | ||
Innym sposobem prezentacji charakterystyk amplitudowo-fazowej są wykresy Nicholsa <math>A=f(\varphi)</math> w których na soi ox odkłada się przesunięcie fazowe <math>\varphi(\omega)</math> a na osi oy wzmocnienie <math>A(\omega)</math> w skali logarytmicznej. | |||
W praktyce zamiast charakterystyki częstotliwościowej zaprezentowanej na płaszczyźnie zespolonej używa się dwóch oddzielnych charakterystyk zaprezentowanych w skali logarytmicznej: | |||
*logarytmiczna charakterystyka amplitudowa – jest logarytmicznym modułem wzmocnienia <math>20 \cdot log_{10}|G(j\omega)|</math> gdzie <math>|G(j\omega)|=A(\omega)</math> w logarytmicznej skali pulsacji <math>\omega</math>. Wzmocnienie podawane jest w decybelach [dB], | |||
*logarytmiczna charakterystyka fazowa – jest zależnością argumentu transmitancji widmowej <math>\varphi(\omega)</math> wykreślonej w logarytmicznej skali pulsacji <math>\omega</math>. | |||
często nazywanie charakterystykami Bodego. Zasadniczą zaletą charakterystyk logarytmicznych jest łatwość określania charakterystyki wypadkowej całego układu, gdzie transmitancja stanowi iloczyn transmitancji członów składowych. Wykonuje się to przez zastąpienie mnożenia transmitancji operacja sumowania. | |||
|} | |} | ||
Wersja z 13:38, 29 sie 2006
wersja beta
LABORATORIUM WIRTUALNE 2
Ćwiczenie 2 - System pomiarowy do wyznaczania charakterystyk układów aktywnych

|

|
Plan i przebieg ćwiczenia. |

|
Szczegółowy plan części pierwszej ćwiczenia polegającej na wyznaczenie charakterystyk amplitudowych i fazowych filtrów. |

|
Szczegółowy plan części drugiej ćwiczenia polegającego na pomiarze podstawowych parametrów akustycznego wzmacniacza mocy. |

|
|
Na slajdzie został przedstawiony przykład członu inercyjnego 1 rzędu oraz jego transmitancja. |
|
Na slajdzie został przedstawiony przykład członu rzeczywistego różniczkującego oraz jego transmitancja. |

|

|
W zależności od zastosowanego sygnału wejściowego można wyróżnić następujące charakterystyki czasowe:
|

|
Charakterystyka skokowa jest odpowiedzią układu h(t) na którego wejście podano sygnał skokowy przy zerowych warunkach początkowych. |

|
Charakterystyka liniowo-czasowa jest odpowiedzią układu na wejście którego podano sygnał liniowo zależny od czasu. |

|
|
W ogólnym przypadku sygnał wyjściowy będzie posiadał inną amplitudę i będzie przesunięty w fazie względem sygnału wejściowego. |

|
|

|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|

|
| Plik:LW2 M2 Slajd55.png |

|

|

|

|

|

|

|

|

|