TC Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 21: | Linia 21: | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd3.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd3.png]] | ||
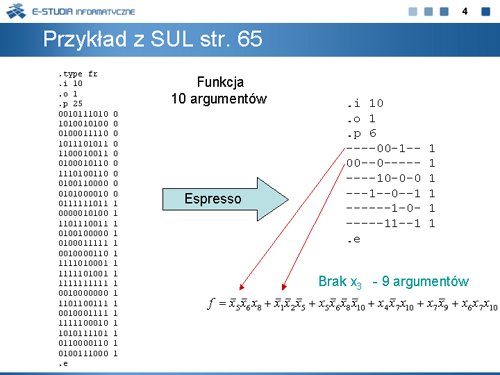
|valign="top"|Celem wprowadzenia wróćmy do przykładu funkcji omawianej w poprzednim wykładzie. Jej tablica prawdy podana na planszy ma 7 argumentów. Ale na poprzednim wykładzie obliczyliśmy metodą ekspansji, że minimalne wyrażenie boolowskie tej funkcji zawiera wyłącznie 4 argumenty. Gdybyśmy to wiedzieli wcześniej, to zadanie minimalizacji moglibyśmy skutecznie uprościć. Wystarczyłoby w tym celu usunąć z tablicy prawdy tej funkcji kolumny odpowiadające nadmiarowym argumentom. Zatem problem obliczania od jakich argumentów funkcja istotnie zależy jest bardzo ważny w zmniejszaniu złożoności obliczeniowej procedur minimalizacji. | |valign="top"|Celem wprowadzenia wróćmy do przykładu funkcji omawianej w poprzednim wykładzie. Jej tablica prawdy podana na planszy ma 7 argumentów. Ale na poprzednim wykładzie obliczyliśmy metodą ekspansji, że minimalne wyrażenie boolowskie tej funkcji zawiera wyłącznie 4 argumenty. Gdybyśmy to wiedzieli wcześniej, to zadanie minimalizacji moglibyśmy skutecznie uprościć. Wystarczyłoby w tym celu usunąć z tablicy prawdy tej funkcji kolumny odpowiadające nadmiarowym argumentom. Zatem problem obliczania od jakich argumentów funkcja istotnie zależy jest bardzo ważny w zmniejszaniu złożoności obliczeniowej procedur minimalizacji. | ||
|} | |} | ||
| Linia 35: | Linia 36: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd5.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd5.png]] | ||
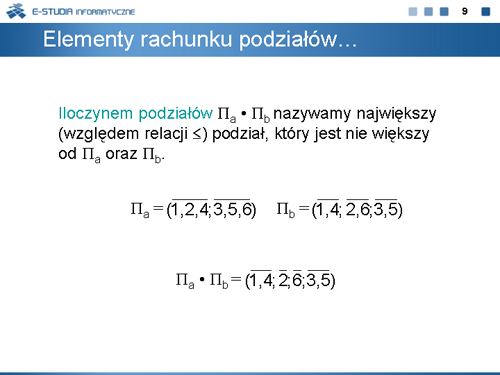
|valign="top"| | |valign="top"|Można jednak obliczyć (programem Pandor), że funkcja ta w rzeczywistości jest zależna od 7 argumentów. Czyli Espresso doskonale redukuje składniki iloczynowe funkcji, ale w przypadku argumentów jego obliczenia nie są skuteczne. Potwierdza to sygnalizowany już mankament metody i programu Espresso. | ||
|} | |} | ||
| Linia 42: | Linia 44: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd6.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd6.png]] | ||
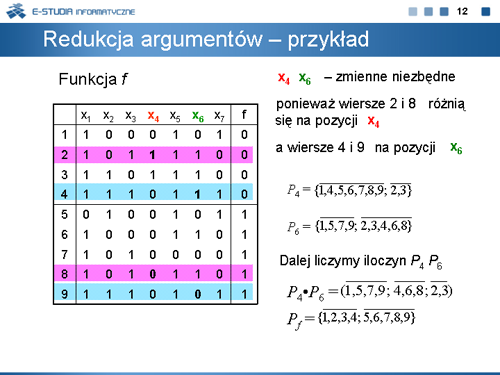
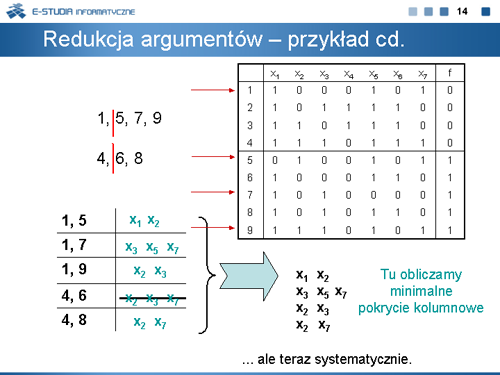
|valign="top"| | |valign="top"|Z powyższych przykładów wynika, że obliczanie minimalnej liczby argumentów | ||
od których funkcja istotnie zależy jest bardzo istotne w redukowaniu złożoności obliczeniowej procedur minimalizacji funkcji boolowskich, a w konsekwencji może się przyczynić do uzyskiwania lepszych rezultatów. Do obliczeń w metodzie redukcji argumentów będziemy stosować rachunek podziałów. Niezbędne pojęcia tego rachunku podajemy na planszach 7, 8 oraz 9. | |||
|} | |} | ||
| Linia 49: | Linia 53: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd7.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd7.png]] | ||
|valign="top"| | |valign="top"|''Podziałem'' na zbiorze <math>S\,</math> jest system zbiorów <math>\pi=\left \{ Bi \right\}\,</math>, którego bloki są rozłączne, czyli | ||
<math>B_i\cap B_j=\varnothing</math> , jeśli tylko <math>i\neq j</math> . | |||
Na przykład dla S = {1,2,3,4,5,6}, P = {{1,2}, {3,5}, {4,6} } jest podziałem na S, co zapisujemy: | |||
:<math>\pi=(\overline{1,2};\overline{3,4};\overline{5,6})</math> | |||
Dla podziałów – podobnie jak dla zbiorów –definiuje się relację porządku oraz typowe działania iloczynu, sumy itp., | |||
|} | |} | ||
| Linia 57: | Linia 70: | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd8.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd8.png]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
Wersja z 19:16, 28 sie 2006

|
Redukcja argumentów |

|
|
|

|

|
|

|
|

|

|

|

|

|

|

|

|