MN04: Różnice pomiędzy wersjami
mNie podano opisu zmian |
mNie podano opisu zmian |
||
| Linia 1: | Linia 1: | ||
''Uwaga: przekonwertowane latex2mediawiki; prawdopodobnie trzeba wprowadzi? poprawki'' | |||
==Ćwiczenia: równania nieliniowe skalarne== | |||
{{cwiczenie|Metoda Newtona może być zbieżna globalnie|| | |||
Wykaż, że jeśli <math>\displaystyle f</math> jest rosnąca i wypukła na <math>\displaystyle [a,b]</math> oraz dla <math>\displaystyle x^*\in [a,b]\displaystyle f(x^*) = 0</math>, to metoda Newtona startująca z <math>\displaystyle x_0>x^*</math> jest zbieżna. | |||
}} | |||
< | |||
< | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
Powtarzając rachunki z dowodu lokalnej zbieżności, możemy łatwo stwierdzić, że kolejne | |||
iteracje dają <math>\displaystyle x_k</math> które także spełniają warunek <math>\displaystyle x_k - x^* > 0</math>. Ponadto | |||
< | nietrudno sprawdzić, że <math>\displaystyle x_{k+1} < x_k</math>, a więc mamy ciąg malejący i | ||
ograniczony. Jego granicą musi być <math>\displaystyle x^*</math> (dlaczego?). | |||
</ | </div></div> | ||
{{cwiczenie|Fraktale|| | |||
Ciekawy zbiór o charakterze fraktalnym powstaje w wyniku zastosowania metody | |||
Newtona do rozwiązania równania <math>\displaystyle z^n-1=0</math> w dziedzinie zespolonej. Punkt <math>\displaystyle z_0 = | |||
<math>\displaystyle | (x_0,y_0)</math> należy do ''basenu zbiezności metody'', jeśli metoda Newtona jest | ||
zeń zbieżna do (jakiegokolwiek) pierwiastka w/w równania. Kolor odpowiadający | |||
<math>\displaystyle z_0</math> jest określany na podstawie liczby iteracji potrzebnych metodzie do | |||
zbieżności. | |||
Zupełnie miłym (i estetycznie wartościowym) doświadczeniem, jest napisanie | |||
programu w Octave, który wyświetla baseny zbieżności metody Newtona jak poniżej. | |||
[[Image:MNfraktal.png|400px|Basen zbiezności metody Newtona w okolicy początku układu | |||
współrzędnych, dla równania <math>\displaystyle z^5-1=0</math>]] | |||
\ | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | |||
Bardzo wygodnie napisać taki program w postaci skryptu Octave. Pamiętaj | |||
jednak, by uniknąć w nim pętli w rodzaju | |||
for xpixels <nowiki>=</nowiki> 1:1024<br> | |||
for ypixels <nowiki>=</nowiki> 1:768<br> | |||
... wyznacz kolor pixela ....<br> | |||
end<br> | |||
end<br> | |||
Taka podwójnie zagnieżdżona pętla może skutecznie zniechęcić Cię do | |||
Octave'a --- obrazek będzie liczyć się wieki --- zupełnie niepotrzebnie! | |||
</div></div> | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | |||
Kluczem do efektywnej implementacji w Octave jest przeprowadzenie | |||
iteracji Newtona na ''wszystkich pikselach jednocześnie''. W tym celu musisz | |||
skorzystać z prowadzenia działań na całych macierzach. | |||
</div></div> | |||
}} | |||
{{cwiczenie|Pierwiastkowanie|| | |||
| | |||
Niech <math>\displaystyle a\geq 0</math>. Aby wyznaczyć <math>\displaystyle \sqrt{a}</math>, można skorzystać z metody Newtona dla | |||
równania <math>\displaystyle x^2 = a</math>. Zaprogramuj tę metodę i sprawdź, jak wiele dokładnych cyfr | |||
wyniku dostajesz w kolejnych krokach. Czy to możliwe, by liczba dokładnych cyfr | |||
znaczących z grubsza podwajała się na każdej iteracji? Wskaż takie <math>\displaystyle a</math> dla | |||
którego to nie będzie prawdą. | |||
==== | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Na pewno kusi Cię, by zaprogramować najpierw ogólnie funkcję "metoda | |||
Newtona", a następnie przekazać jej jako parametr naszą funkcję. To oczywiście | |||
będzie działać, i to praktycznie tak samo szybko jak drugi spsoób, w którym po prostu | |||
wyliczysz na karteczce wzór na iterację dla ''tej konkretnej funkcji, <math>\displaystyle F(x) = | |||
x^2-a</math>'' i potem go zaimplementujesz. Jednak | |||
drugie podejście jest tutaj godne polecenia, bo ma na sobie znak charakterystyczny dla numeryki: niech | |||
wszystko, co programujesz będzie tak proste, jak tylko możliwe (ale nie | |||
prostsze)! | |||
</div></div> | |||
}} | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
Nasza iteracja, którą chcemy zaprogramować, to | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
x_{k+1} = \frac{1}{2}\left( x_k + \frac{a}{x_k}\right). | |||
</math></center> | |||
Dla <math>\displaystyle a\neq 0</math>, spełnione są założenia twierdzenia o zbieżności metody Newtona, | |||
więc | |||
<center><math>\displaystyle |x_{k+1}-x^*|\leq K |x_{k}-x^*|^2 | |||
</math></center> | </math></center> | ||
co właśnie tłumaczy się jako podwajanie liczby dokładnych cyfr | |||
znaczących wyniku. | |||
Ale jeśli <math>\displaystyle a=0</math> to metoda zbieżna jest już tylko liniowo (z ilorazem 0.5 --- bo | |||
jaki wtedy jest wzór na iterację?), więc co mniej więcej trzy kroki będziemy | |||
dostawali kolejne zero dokładnego wyniku <math>\displaystyle x^*=0</math>. | |||
</div></div> | |||
{{cwiczenie|Odwrotność bez dzielenia|| | |||
Aby wyznaczyć <math>\displaystyle 1/a</math> dla <math>\displaystyle a>0</math> bez dzielenia(!), można zastosować metodę Newtona | |||
do funkcji <math>\displaystyle f(x) = 1/x - a</math>. Pokaż, że na <math>\displaystyle k</math>-tym kroku iteracji, | |||
<center><math>\displaystyle | <center><math>\displaystyle | ||
|ax_k - 1| = |ax_{k-1} - 1|^2. | |||
</math></center> | </math></center> | ||
Dla jakich <math>\displaystyle x_0</math> metoda będzie zbieżna do <math>\displaystyle \frac{1}{a}</math>, a dla jakich nie? | |||
Oceń, ile iteracji potrzeba do spełnienia warunku <math>\displaystyle \frac{|x_k-\frac{1}{a}|}{|a|} \leq | |||
\epsilon</math>, gdy <math>\displaystyle \frac{|x_0-\frac{1}{a}|}{|a|} \leq \gamma < 1</math>, | |||
}} | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
Proste ćwiczenie z analizy. Warunkiem zbieżności jest oczywiście (ze względu na | |||
równość w wyrażeniu na błąd iteracji powyżej) <math>\displaystyle |ax_0 - 1| < 1</math>, to znaczy | |||
<center><math>\displaystyle 0 < x_0 < \frac{2}{a}.</math></center> | |||
</div></div> | |||
< | {{cwiczenie||| | ||
Zaimplementuj metodę bisekcji. Sprawdź, jak będzie działać m.in. dla funkcji | |||
* <math>\displaystyle f(x) = \sin(x)</math>, | |||
* <math>\displaystyle f(x) = \sin^2(x)</math>, | |||
* <math>\displaystyle f(x) = (x-1)^5</math> (wzór A), | |||
* <math>\displaystyle f(x) = (x-1)*(x^4 - 4x^3 + 6x^2 - 4x + 1)</math> (wzór B), | |||
* <math>\displaystyle f(x) = (x-2)^13</math> (wzór C), | |||
* <math>\displaystyle f(x) = x^13 - 26*x^12 + 312*x^11 - 2288*x^10 + ... - 8192</math> (wzór D), | |||
gdy tolerancję błędu zadasz na poziomie <math>\displaystyle 10^{-10}</math>. | |||
Jak wyjaśnić te wyniki? Czy możesz już być pewna, że masz dobrą implementację? | |||
}} | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
Jeśli nie pomylisz się, metoda powinna zbiegać bez problemów do zera funkcji | |||
<math>\displaystyle \sin</math>, dawać komunikat o błędzie dla <math>\displaystyle \sin^2</math> (bo nie ma przeciwnych znaków). | |||
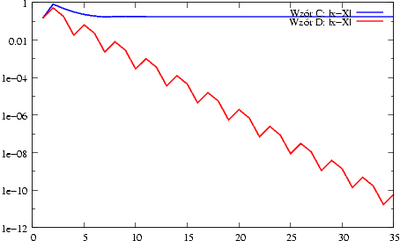
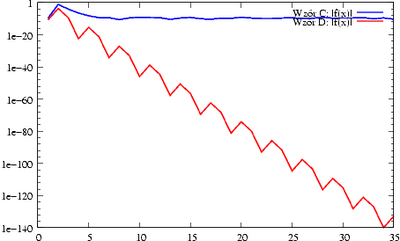
< | Zapewne zauważyłaś, że wzory A i B są matematycznie równoważne, podobnie zresztą | ||
jak wzory C i D. Niestety, tylko wzór A i C dają w efekcie dobre przybliżenia | |||
miejsca zerowego, podczas gdy wzory B i D prowadzą do oszacowania na miejsce | |||
zerowe, które ''w ogóle nie zawierają'' prawdziwego miejsca zerowego. | |||
Wyjaśnieniem tego fenomenu jest zjawisko redukcji cyfr przy odejmowaniu. | |||
< | |||
[[Image:MNbisekcjawblad.png|400px|Metoda bisekcji ma kłopoty, gdy funkcja zadana jest | |||
wzorem D.]] | |||
[[Image:MNbisekcjawresid.png|400px|Residuum też jest duże, gdy <math>\displaystyle f</math> zadana jest | |||
wzorem D.]] | |||
Jeśli chodzi o pewność... No cóż, sprawdziłaś, że działa w przypadkach, gdy | |||
spodziewałaś się, że będzie działać. Że tam, gdzie spodziewałaś się kłopotów, | |||
lub komunikatu o błędzie --- tak rzeczywiście się stało. Wreszcie, | |||
potwierdziłaś, że zachowanie metody jest zgodne z jej znanymi właściwościami. | |||
Tak więc, można ''przypuszczać'', że implementacja jest poprawna. | |||
</div></div> | |||
{{cwiczenie||| | |||
Wskaż ''wszystkie'' wartości <math>\displaystyle x_0</math>, dla jakich metoda Newtona będzie zbieżna | |||
do rozwiązania <math>\displaystyle x^*</math> równania | |||
<center><math>\displaystyle \arctan(x) = 0. | |||
</math></center> | |||
Wyznacz wartość <math>\displaystyle X_0</math>, z którego startując powinieneś dostać ciąg oscylujący <math>\displaystyle X_0, -X_0,\ldots</math>. | |||
Sprawdź eksperymentalnie, czy tak jest rzeczywiście. | |||
<div class=" | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Aby znaleźć graniczne <math>\displaystyle X_0</math>, czyli takie, dla którego dostaniesz | |||
oscylacje <math>\displaystyle X_0, -X_0,\ldots</math>, musisz rozwiązać równanie nieliniowe: | |||
<center><math>\displaystyle -X_0 = X_0 - \frac{\arctan(X_0)}{\frac{1}{1+X_0^2}}. | |||
</math></center> | |||
To łatwe. | |||
</div></div> | |||
}} | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
Dla <math>\displaystyle -X_0 < x_0 < X_0</math> mamy zbieżność. Dla <math>\displaystyle |x_0| = |X_0|</math> oscylacje, dla | |||
większych wartości --- rozbieżność. Jednak w eksperymencie wszystko zależy od | |||
tego, jak dokładnie wyznaczyliśmy <math>\displaystyle X_0</math>. Na przykład, mój solver w Octave | |||
wyznaczył wartość <math>\displaystyle X_0</math>, dla której metoda Newtona dała następujący ciąg: | |||
<div class="output" style="background-color:#e0e8e8; padding:1em"><pre> | |||
</ | |||
Iteracja: 1, x <nowiki>=</nowiki> -1.39175 | |||
Iteracja: 2, x <nowiki>=</nowiki> 1.39175 | |||
Iteracja: 3, x <nowiki>=</nowiki> -1.39175 | |||
Iteracja: 4, x <nowiki>=</nowiki> 1.39175 | |||
Iteracja: 5, x <nowiki>=</nowiki> -1.39175 | |||
.. itd .. | |||
< | Iteracja: 25, x <nowiki>=</nowiki> -1.39176 | ||
Iteracja: 26, x <nowiki>=</nowiki> 1.39178 | |||
Iteracja: 27, x <nowiki>=</nowiki> -1.39183 | |||
Iteracja: 28, x <nowiki>=</nowiki> 1.39197 | |||
Iteracja: 29, x <nowiki>=</nowiki> -1.39235 | |||
Iteracja: 30, x <nowiki>=</nowiki> 1.39333 | |||
Iteracja: 31, x <nowiki>=</nowiki> -1.39594 | |||
Iteracja: 32, x <nowiki>=</nowiki> 1.40283 | |||
Iteracja: 33, x <nowiki>=</nowiki> -1.42117 | |||
Iteracja: 34, x <nowiki>=</nowiki> 1.47061 | |||
Iteracja: 35, x <nowiki>=</nowiki> -1.60867 | |||
Iteracja: 36, x <nowiki>=</nowiki> 2.03161 | |||
Iteracja: 37, x <nowiki>=</nowiki> -3.67722 | |||
Iteracja: 38, x <nowiki>=</nowiki> 15.2779 | |||
Iteracja: 39, x <nowiki>=</nowiki> -337.619 | |||
Iteracja: 40, x <nowiki>=</nowiki> 178376 | |||
Iteracja: 41, x <nowiki>=</nowiki> -4.99792e+10 | |||
Iteracja: 42, x <nowiki>=</nowiki> 3.92372e+21 | |||
Iteracja: 43, x <nowiki>=</nowiki> -2.41834e+43 | |||
Iteracja: 44, x <nowiki>=</nowiki> 9.18658e+86 | |||
Iteracja: 45, x <nowiki>=</nowiki> -1.32565e+174 | |||
Iteracja: 46, x <nowiki>=</nowiki> inf | |||
Iteracja: 47, x <nowiki>=</nowiki> nan | |||
</pre></div> | </pre></div> | ||
</div></div> | |||
Wersja z 16:33, 28 sie 2006
Uwaga: przekonwertowane latex2mediawiki; prawdopodobnie trzeba wprowadzi? poprawki
Ćwiczenia: równania nieliniowe skalarne
Ćwiczenie Metoda Newtona może być zbieżna globalnie
Wykaż, że jeśli jest rosnąca i wypukła na oraz dla , to metoda Newtona startująca z jest zbieżna.
Ćwiczenie Fraktale
Ćwiczenie Pierwiastkowanie
Ćwiczenie Odwrotność bez dzielenia
Aby wyznaczyć dla bez dzielenia(!), można zastosować metodę Newtona do funkcji . Pokaż, że na -tym kroku iteracji,
Dla jakich metoda będzie zbieżna do , a dla jakich nie? Oceń, ile iteracji potrzeba do spełnienia warunku , gdy ,
Ćwiczenie
Zaimplementuj metodę bisekcji. Sprawdź, jak będzie działać m.in. dla funkcji
- ,
- ,
- (wzór A),
- (wzór B),
- (wzór C),
- (wzór D),
gdy tolerancję błędu zadasz na poziomie .
Jak wyjaśnić te wyniki? Czy możesz już być pewna, że masz dobrą implementację?
Ćwiczenie