PEE Moduł 10

Wykład10. Czwórniki

---

Definicja czwórnika Czwórnik jest elementem czterozaciskowym, mającym dwie pary uporządkowanych zacisków, z których jedna para jest wejściem a druga para wyjściem Oznaczenie czwórnika z zaznaczonymi zwrotami prądów i napięć końcówkowych jest przedstawione na rysunku na slajdzie 2. W odniesieniu do wejścia i wyjścia czwórnika musi być spełniony warunek równości prądów: $I_1=I_1^{\text{'}}$ $I_2=I_2^{\text{'}}$ jak to zaznaczono na rysunku. Sygnały prądu i napięcia po stronie wejściowej oznaczać będziemy ze wskaźnikiem 1, a po stronie wyjściowej – ze wskaźnikiem 2. Przyjmiemy umownie, że oba prądy: na wejściu i wyjściu są zwrócone do prostokąta oznaczającego czwórnik. W zależności od elementów tworzących obwód, czwórnik może być liniowy (gdy wszystkie elementy obwodu są liniowe) lub nieliniowy. W dalszych rozważaniach ograniczymy się wyłącznie do czwórników liniowych. Czwórnik nazywać będziemy pasywnym, jeśli nie wytwarza energii a jedynie pobiera ją ze źródła zasilającego i przetwarza w określony sposób. Czwórnik złożony z samych elementów pasywnych R, L, C i M jest zawsze czwórnikiem pasywnym. Czwórnik pasywny jest zdolny do gromadzenia i rozpraszania energii pobranej ze źródła, może ją również oddawać na zewnątrz, jednak w dowolnej chwili czasowej $t$ energia ta nie może przewyższać energii pobranej. Czwórnik, który nie spełnia powyższych warunków jest czwórnikiem aktywnym (generatorem energii).

---

Równania czwórnika Czwórnik może być scharakteryzowany za pomocą równań liniowych wiążących ze sobą dwie wielkości prądowe i dwie napięciowe dotyczące bramy wejściowej i wyjściowej: $I_1$, $I_2$, $U_1$ oraz $U_2$. W zależności od wyboru zmiennych można wyróżnić 6 podstawowych postaci równań czwórnika. Są to postać admitancyjna, w której prądy wejściowy i wyjściowy ($I_1,I_2$) są wyrażone w zależności od napięć zewnętrznych ($U_1,U_2$) postać impedancyjna, w której napięcia wejściowe i wyjściowe ($U_1,U_2$) są wyrażone w zależności od prądów końcówkowych ($I_1,I_2$) postać hybrydowa w której para wielkości ($U_1,I_2$) jest wyrażona jako funkcja drugiej pary ($I_1,U_2$) postać hybrydowa odwrotna w której para wielkości ($I_1,U_2$) jest wyrażona jako funkcja drugiej pary ($U_1,I_2$) postać łańcuchowa w której para wielkości ($U_1,I_1$) dotycząca zacisków wejściowych jest wyrażona jako funkcja drugiej pary ($U_2,I_2$) związanej z zaciskami wyjściowymi postać łańcuchowa odwrotna w której para wielkości ($U_2,I_2$) dotycząca zacisków wyjściowych jest wyrażona jako funkcja drugiej pary ($U_1,I_1$) związanej z zaciskami wejściowymi.

---

Równanie admitancyjne Jeżeli za zmienne niezależne przyjmie się napięcia obu bram $U_1$ oraz $U_2$ czwórnik przyjmie opis admitancyjny, który można wyrazić w postaci $\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\left[\begin{array}{cc}{Y}_{11}& Y_{12}\\ Y_{21}& Y_{22}\end{array}\right]\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]=\mathbf{𝐘}\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]$ Macierz $\mathbf{𝐘}$ jest nazywana macierzą admitancyjną a parametry tej macierzy mają interpretację admitancji operatorowych. Równanie impedancyjne Jeżeli za zmienne niezależne przyjmie się prądy obu bram $I_1$ oraz $I_2$ , czwórnik przyjmie opis impedancyjny, który można wyrazić w postaci $\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]=\left[\begin{array}{cc}{Z}_{11}& Z_{12}\\ Z_{21}& Z_{22}\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\mathbf{𝐙}\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]$ Macierz $\mathbf{𝐙}$ jest nazywana macierzą impedancyjną a parametry tej macierzy mają interpretację impedancji operatorowych. Łatwo jest udowodnić, że macierze impedancyjna i admitancyjna są powiązane relacją $\mathbf{𝐘}={\mathbf{𝐙}}^{-1}$ Równanie łańcuchowe Równanie łańcuchowe czwórnika uzależnia prąd i napięcie na wejściu czwórnika od prądu i napięcia na jego wyjściu $\left[\begin{array}{c}{U}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right]\left[\begin{array}{c}{U}_2\\ -I_2\end{array}\right]=\mathbf{𝐀}\left[\begin{array}{c}{U}_2\\ -I_2\end{array}\right]$ W równaniu tym, inaczej niż w pozostałych opisach, przyjmuje się prąd $I_2$ wypływający z czwórnika, w związku z czym przy założonym na wstępie zwrocie prądu do czwórnika w opisie pojawia się prąd wyjściowy ze znakiem minus. Elementy macierzy łańcuchowej A nazywane są parametrami łańcuchowymi czwórnika.

---

Równania hybrydowe Przy opisie hybrydowym za zmienne niezależne wybiera się prąd wejściowy i napięcie wyjściowe czwórnika. Równanie hybrydowe przyjmuje się w postaci $\left[\begin{array}{c}{U}_1\\ I_2\end{array}\right]=\left[\begin{array}{cc}{H}_{11}& H_{12}\\ H_{21}& H_{22}\end{array}\right]\left[\begin{array}{c}{I}_1\\ U_2\end{array}\right]=\mathbf{𝐇}\left[\begin{array}{c}{I}_1\\ U_2\end{array}\right]$ w której $\mathbf{𝐇}$ jest macierzą hybrydową. Jak widać z opisu hybrydowego parametr $H_{11}$ ma interpretację impedancji a $H_{22}$ admitancji. Parametry $H_{12}$ i $H_{21}$ są bezwymiarowe i wyrażają stosunek odpowiednio dwu napięć i dwu prądów w obwodzie. Zamieniając zmienne wejściowe i wyjściowe otrzymuje się opis hybrydowy odwrotny czwórnika w postaci $\left[\begin{array}{c}{I}_1\\ U_2\end{array}\right]=\left[\begin{array}{cc}{G}_{11}& G_{12}\\ G_{21}& G_{22}\end{array}\right]\left[\begin{array}{c}{U}_1\\ I_2\end{array}\right]=\mathbf{𝐆}\left[\begin{array}{c}{U}_1\\ I_2\end{array}\right]$ Stanowi on odwrotność opisu hybrydowego macierzą $\mathbf{𝐇}$. Obie macierze powiązane są następująca relacją $\mathbf{𝐆}={\mathbf{𝐇}}^{-1}$ Duża liczba stosowanych opisów macierzowych czwórnika wynika również z faktu, że dla niektórych czwórników pewne opisy mogą nie istnieć. Najbardziej uniwersalne pod tym względem są opisy hybrydowe wykorzystujące macierz $\mathbf{𝐇}$ lub $\mathbf{𝐆}$, które można otrzymać dla większości obwodów elektrycznych.

---

Jako przykład wyznaczymy opis czwórnika przedstawionego na rysunku na slajdzie 6. Czwórnik ten nosi nazwę czwórnika typu $T$ i jest jedną z najpopularniejszych struktur czwórnikowych. Rozwiązanie Z prawa napięciowego i prądowego Kirchhoffa zastosowanego do obwodu z rysunku można napisać następujące równania $I_1=I-I_2=Y{U}_2+(1+Z_{2}Y)(-I_2)$ $U_1=U_2+Z_1{I}_1-Z_2{I}_2$ Po podstawieniu równania pierwszego do drugiego otrzymuje się $U_1=(1+Z_{1}Y)U_2+(Z_1+Z_2+Z_1{Z}_{2}Y)(-I_2)$ Jeśli jako opis macierzowy przyjmiemy równanie łańcuchowe to zależności określające prąd wejściowy i napięcie wejściowe w funkcji prądu i napięcia wyjściowego można zapisać w postaci $\left[\begin{array}{c}{U}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}1+Z_{1}Y& Z_1+Z_2+Z_1{Z}_{2}Y\\ Y& 1+Z_{2}Y\end{array}\right]\left[\begin{array}{c}{U}_2\\ -I_2\end{array}\right]$ Macierz łańcuchowa $\mathbf{𝐀}$ dana jest więc wzorem $\mathbf{𝐀}=\left[\begin{array}{cc}1+Z_{1}Y& Z_1+Z_2+Z_1{Z}_{2}Y\\ Y& 1+Z_{2}Y\end{array}\right]$ Jeśli jako opis macierzowy przyjmiemy równanie impedancyjne, wówczas z przetworzenia równania łańcuchowego otrzymujemy $\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]=\left[\begin{array}{cc}Z+Z_1& Z\\ Z& Z+Z_2\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]$ Macierz impedancyjna dana jest więc w postaci $\mathbf{𝐙}=\left[\begin{array}{cc}Z+Z_1& Z\\ Z& Z+Z_2\end{array}\right]$ Jest to macierz symetryczna, która jest równa macierzy oczkowej obwodu tworzącego analizowany czwórnik.

---

Pokażemy związek opisu transmitancyjnego z parametrami macierzowymi czwórnika. Transmitancja napięciowa Weźmy pod uwagę transmitancję napięciową, jako stosunek napięcia wyjściowego do napięcia wejściowego w dziedzinie operatorowej przy założeniu zerowego prądu obciążenia czwórnika ($I_2(s)=0$) $T_u(s)=\frac{U_2(s)}{U_1(s)}$ Z równania łańcuchowego, wobec $I_2(s)=0$ otrzymujemy $U_1(s)=A_{11}{U}_2(s)$ Stąd $T_u(s)=\frac{U_2(s)}{U_1(s)}=\frac{1}{A_{11}}$ O transmitancji napięciowej decyduje jeden parametr łańcuchowy $A_{11}$ czwórnika. W identyczny sposób uzyskać można relację wiążącą transmitancję napięciową z parametrami dowolnego opisu czwórnikowego. Przykładowo na podstawie opisu admitancyjnego z równania drugiego czwórnika, wobec $I_2=0$, wynika $I_2=Y_{21}{U}_1+Y_{22}{U}_2=0$ Stąd $T_u(s)=\frac{U_2(s)}{U_1(s)}=-\frac{Y_{21}}{Y_{22}}$

---

Impedancja wejściowa Określenie funkcji impedancji wejściowej układu czwórnika wymaga ustalenia przy jakiej impedancji obciążenia badany jest czwórnik. Załóżmy w ogólności obciążenie czwórnika impedancją Zo. Z równań łańcuchowych czwórnika otrzymuje się $U_1(s)=A_{11}{U}_2(s)+A_{12}(-I_2(s))=A_{11}{U}_2(s)+A_{12}{Y}_0{U}_2(s)$ $I_1(s)=A_{21}{U}_2(s)+A_{22}(-I_2(s))=A_{21}{U}_2(s)+A_{22}{Y}_0{U}_2(s)$ gdzie $Y_0$ oznacza admitancję obciążenia (odwrotność impedacji $Z_0$, $Y_0=1/Z_0$). Z powyższych równań otrzymuje się $Z_{we}(s)=\frac{U_1(s)}{I_1(s)}=\frac{A_{11}+A_{12}{Y}_0}{A_{21}+A_{22}{Y}_0}$ Impedancja wejściowa czwórnika obciążonego jest funkcją wszystkich parametrów łańcuchowych tego czwórnika. Pewne uproszczenia powstają w stanach szczególnych obciążeń. Na przykład w stanie jałowym na zaciskach wyjściowych ($Y_0=0$) $Z_{we}(s)=\frac{A_{11}}{A_{21}}$ oraz w stanie zwarcia na wyjściu ($Y_0=\mathrm{\infty }$) $Z_{we}(s)=\frac{A_{12}}{A_{22}}$ impedancja wejściowa zależy wyłącznie od dwóch parametrów łańcuchowych. Identyczne zależności określające impedancje wejściową otrzymać można na podstawie dowolnego opisu czwórnikowego.

---

Wyznaczyć wyrażenie na transmitancję napięciową i impedancję wejściową czwórnika z poprzedniego przykładu. Rozwiązanie Macierz łańcuchowa czwórnika ma postać $\mathbf{𝐀}=\left[\begin{array}{cc}1+Z_{1}Y& Z_1+Z_2+Z_1{Z}_{2}Y\\ Y& 1+Z_{2}Y\end{array}\right]$ Transmitancja napięciowa w stanie jałowym na wyjściu jest więc równa $T_u(s)=\frac{U_2(s)}{U_1(s)}=\frac{1}{A_{11}}=\frac{1}{1+Z_{1}Y}=\frac{Z}{Z+Z_1}$ Wobec braku obciążenia czwórnika przez impedancję $Z_2$ nie przepływa prąd, stąd całe napięcie wyjściowe pochodzi z impedancji poprzecznej $Z$ (dzielnik impedancyjny). Impedancja wejściowa czwórnika przy obciążeniu bramy wyjściowej impedancją $Z_0$ na podstawie wzoru jest równa $Z_{we}(s)=\frac{U_1(s)}{I_1(s)}=\frac{A_{11}+A_{12}{Y}_0}{A_{21}+A_{22}{Y}_0}=\frac{(1+Z_{1}Y)+(Z_1+Z_2+Z_1{Z}_{2}Y)Y_0}{Y+(1+Z_{2}Y)Y_0}$ Jest ona funkcją wszystkich parametrów układu oraz impedancji obciążenia.

---

Połączenie łańcuchowe, zwane również kaskadowym czwórników to takie połączenie , w którym zaciski wejściowe jednego czwórnika są przyłączone do zacisków wyjściowych poprzedniego. Przykład połączenia łańcuchowego dwu czwórników przedstawiony jest na rysunku obok. Łatwo jest pokazać, że macierz łańcuchowa $\mathbf{𝐀}$ czwórników połączonych kaskadowo jest równa iloczynowi macierzy łańcuchowych poszczególnych czwórników tworzących to połączenie $\mathbf{𝐀}={\mathbf{𝐀}}_1\cdot {\mathbf{𝐀}}_2$ Przy większej liczbie czwórników połączonych kaskadowo macierz łańcuchowa wypadkowa jest równa iloczynowi macierzy łańcuchowych wszystkich czwórników branych w kolejności ich występowania w łańcuchu. $\mathbf{𝐀}={\mathbf{𝐀}}_1{\mathbf{𝐀}}_2\cdots {\mathbf{𝐀}}_n$ Należy zwrócić uwagę, że przy mnożeniu macierzy istotna jest kolejność tych macierzy, gdyż w ogólności ${\mathbf{𝐀}}_1\cdot {\mathbf{𝐀}}_2\ne {\mathbf{𝐀}}_2\cdot {\mathbf{𝐀}}_1$

---

Dwa czwórniki są połączone szeregowo, jeśli spełnione są warunki: prąd wejściowy jednego czwórnika jest równy prądowi wejściowemu drugiego a prąd wyjściowy jednego czwórnika jest równy prądowi wyjściowemu drugiego napięcie wejściowe (wyjściowe) połączenia jest równe sumie napięć wejściowych (wyjściowych) każdego czwórnika. Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo, spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu szeregowym czwórników macierz impedancyjna $\mathbf{𝐙}$ połączenia jest równa sumie macierzy impedancyjnych każdego czwórnika. Oznacza to, że $\mathbf{𝐙}={\mathbf{𝐙}}_1+{\mathbf{𝐙}}_2$ Przy większej liczbie czwórników połączonych szeregowo macierz impedancyjna wypadkowa jest równa sumie macierzy impedancyjnych wszystkich czwórników występujących w połączeniu. $\mathbf{𝐙}=\sum _{i=1}^n{\mathbf{𝐙}}_i$ Kolejność sumowania macierzy impedancyjnych nie odgrywa żadnej roli.

---

Dwa czwórniki są połączone równolegle, jeśli spełnione są warunki: napięcie wejściowe każdego czwórnika jest takie samo, podobnie napięcie wyjściowe prąd wejściowy (wyjściowy) połączenia jest równy sumie prądów wejściowych (wyjściowych) każdego czwórnika. Ponadto w tym przypadku należy zapewnić spełnienie warunków regularności połączenia zdefiniowanych odpowiednią równością prądów. Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu równoległym czwórników macierz admitancyjna $\mathbf{𝐘}$ połączenia jest równa sumie macierzy admitancyjnych każdego czwórnika. Oznacza to, że $\mathbf{𝐘}={\mathbf{𝐘}}_1+{\mathbf{𝐘}}_2$ Przy większej liczbie czwórników połączonych równolegle macierz admitancyjna wypadkowa jest równa sumie macierzy admitancyjnych wszystkich czwórników występujących w połączeniu. $\mathbf{𝐘}=\sum _{i=1}^n{\mathbf{𝐘}}_i$ Kolejność sumowania macierzy admitancyjnych nie odgrywa żadnej roli.

---

Dwa czwórniki są połączone szeregowo-równolegle, jeśli spełnione są warunki: prąd wejściowy każdego czwórnika jest taki sam a napięcie wejściowe połączenia jest równe sumie napięć wejściowych każdego czwórnika prąd wyjściowy połączenia jest równy sumie prądów wyjściowych każdego czwórnika a napięcie wyjściowe obu czwórników jest takie samo. Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów. Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo-równolegle (szeregowo po stronie zacisków wejściowych i równolegle po stronie zacisków wyjściowych), spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu szeregowo-równoległym czwórników macierz hybrydowa $H$ połączenia jest równa sumie macierzy hybrydowych $\mathbf{𝐇}$ każdego czwórnika. Oznacza to, że $\mathbf{𝐇}={\mathbf{𝐇}}_1+{\mathbf{𝐇}}_2$ Przy większej liczbie czwórników połączonych szeregowo-równolegle macierz hybrydowa $\mathbf{𝐇}$, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych $\mathbf{𝐇}$ wszystkich czwórników występujących w połączeniu. $\mathbf{𝐇}=\sum _{i=1}^n{\mathbf{𝐇}}_i$ Kolejność sumowania macierzy hybrydowych nie odgrywa żadnej roli.

---

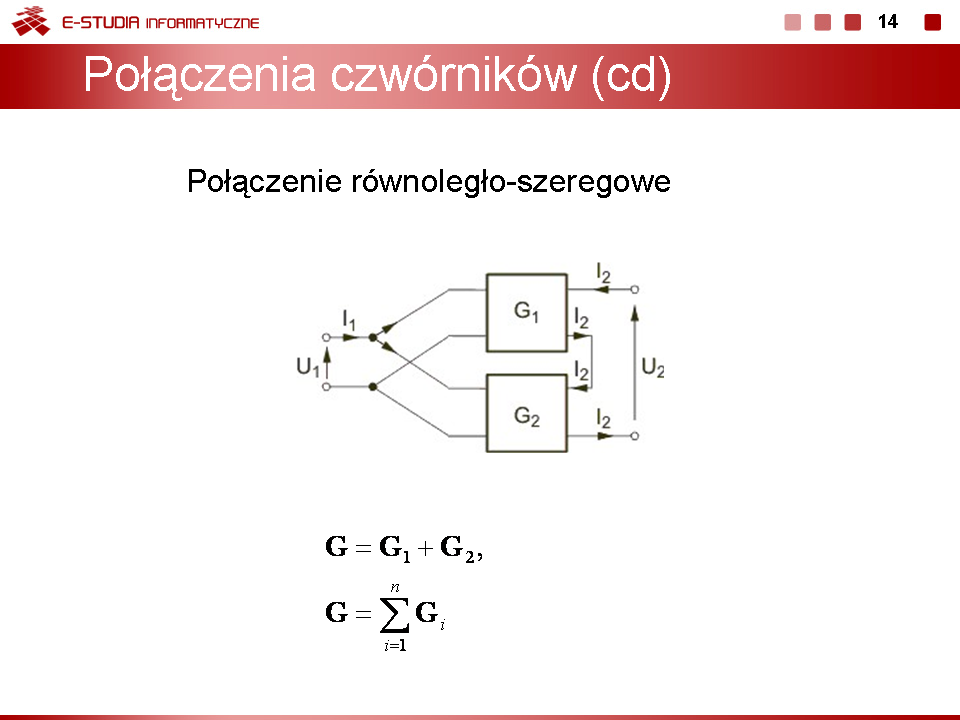
Dwa czwórniki są połączone równolegle-szeregowo, jeśli spełnione są warunki: napięcie wejściowe każdego czwórnika jest takie samo a prąd wejściowy połączenia jest równy sumie prądów wejściowych każdego czwórnika prąd wyjściowy każdego czwórnika jest taki sam a napięcie wyjściowe połączenia jest równe sumie napięć wyjściowych każdego z nich. Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów. Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle-szeregowo (równolegle po stronie zacisków wejściowych i szeregowo po stronie zacisków wyjściowych), spełniający powyższe warunki. Łatwo jest pokazać, że w połączeniu równolegle-szeregowym czwórników macierz hybrydowa odwrotna $\mathbf{𝐆}$ połączenia jest równa sumie macierzy hybrydowych $G$ każdego czwórnika. Oznacza to, że $\mathbf{𝐆}={\mathbf{𝐆}}_1+{\mathbf{𝐆}}_2$ Przy większej liczbie czwórników połączonych równolegle-szeregowo macierz hybrydowa odwrotna $\mathbf{𝐆}$, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych $\mathbf{𝐆}$ wszystkich czwórników występujących w połączeniu. $\mathbf{𝐆}=\sum _{i=1}^n{\mathbf{𝐆}}_i$ Kolejność sumowania macierzy nie odgrywa żadnej roli.

---

Żyrator Żyrator jest czwórnikiem opisanym następującą macierzą łańcuchową $\left[\begin{array}{c}{U}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}0& R_z\\ G_z& 0\end{array}\right]\left[\begin{array}{c}{U}_2\\ -I_2\end{array}\right]$ Parametr $G_z$ jest nazywany konduktancją żyracji a $R_z=1/G_z$ rezystancją. Oznaczenia graficzne żyratora przedstawione są na rysunku obok (slajd 13). Znak minus występujący przy prądzie wyjściowym wynika z przyjętego zwrotu prądu wyjściowego (do pudełka). Równaniu łańcuchowemu żyratora odpowiada opis admitancyjny o postaci $\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\left[\begin{array}{cc}0& G_z\\ -G_z& 0\end{array}\right]\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]$ Najważniejszą własnością żyratora jest przetwarzanie impedancji obciążenia w impedancję odwrotnie proporcjonalną do niej. Rozważmy układ żyratora obciążonego impedancją $Z_0$ (rysunek na slajdzie 14). Impedancja wejściowa takiego układu zdefiniowana w postaci $Z_{we}=\frac{U_1}{I_1}$ $A_{11}=0$, $A_{12}=R_z$, $A_{21}=G_z$, $A_{22}=0$, więc $Z_{we}=\frac{A_{11}+A_{12}{Y}_0}{A_{21}+A_{22}{Y}_0}=\frac{R_z^2}{Z_0}$

---

Impedancja układu żyratora obciążonego impedancją $Z_0$ jest odwrotnie proporcjonalna do impedancji obciążenia ze współczynnikiem proporcjonalności równym $R_z^2$. Jeśli żyrator zostanie obciążony kondensatorem o impedancji operatorowej równej $Z_0=1/sC$ to impedancja wejściowa układu jest równa $Z_{we}=s{R}_z^{2}C$ Jest to postać odpowiadająca ogólnemu opisowi impedancji operatorowej cewki $Z_L=sL$. Zatem układ żyratora obciążonego pojemnością $C$ przedstawia sobą cewkę o indukcyjności $L$ $L=R_z^{2}C$ Powyższej zależności matematycznej można przyporządkować transformację układową zilustrowaną na rysunku obok (slajd 14). Żyrator jako czwórnik jest bardzo łatwo realizowalny w praktyce przy wykorzystaniu układów tranzystorowych lub wzmacniaczy operacyjnych. Z tego względu układy wykorzystujące żyratory są powszechnie stosowane w układach elektronicznych (np. filtrach) eliminując z nich cewki, trudno realizowalne w technologii scalonej.

---

Konwerter ujemno-impedancyjny (NIC) Konwerter ujemno-impedancyjny (NIC) jest czwórnikiem aktywnym (wytwarzającym energię) posiadającym własność przetwarzania prądu bądź napięcia z ujemnym znakiem. Wyróżnia się dwa rodzaje konwerterów ujemno-impedancyjnych NIC z inwersją prądu (INIC) $\left[\begin{array}{c}{U}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& -K_i\end{array}\right]\left[\begin{array}{c}{U}_2\\ -I_2\end{array}\right]$ NIC z inwersją napięcia (VNIC) $\left[\begin{array}{c}{U}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}-K_u& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{U}_2\\ -I_2\end{array}\right]$ Parametr $K$ ($K_i$ dla konwertera ujemno-impedancyjnego prądu oraz $K_u$ dla konwertera ujemno-impedancyjnego napięcia) jest współczynnikiem przetwarzania bądź prądu bądź napięcia. W konwerterze INIC prąd wejściowy jest proporcjonalny do prądu wyjściowego z ujemnym współczynnikiem proporcjonalności Parser nie mógł rozpoznać (błąd składni): {\displaystyle –K_i} przy niezmienionej wartości napięcia wejściowego. W konwerterze VNIC napięcie wejściowe jest proporcjonalne do napięcia wyjściowego z ujemnym współczynnikiem proporcjonalności Parser nie mógł rozpoznać (błąd składni): {\displaystyle –K_u} przy niezmienionym prądzie wejściowym.

---

Konwerter impedancyjny przetwarza impedancję obciążenia w impedancję wejściową z ujemnym znakiem. Rozważmy układ konwertera INIC obciążonego impedancją $Z_0$, przedstawiony na rysunku obok (slajd 16). Wykorzystując równania konwertera i uwzględniając równanie opisujące obciążenie $U_0=Z_0(-I_2)=U_2$ impedancja wejściowa układu dana jest zależnością $Z_{we}=\frac{U_1}{I_1}=\frac{U_2}{-K_i(-I_2)}=-\frac{Z_0}{K_i}$ Jak z powyższego równania wynika konwerter ujemno-impedancyjny obciążony impedancją $Z_0$ reprezentuje sobą (z punktu widzenia wejścia) impedancję ujemną $-\frac{Z_0}{K_i}$. Podobną własność ma konwerter ujemno-impedancyjny napięcia (VNIC). Cecha ta może być wykorzystana do realizacji rezystancji ujemnej. Mianowicie przyjmując obciążenie konwertera rezystancją $Z_0=R_0$ otrzymuje się impedancję wejściową równą $Z_{we}=-R_0/K_i$. Należy pamiętać, że ujemna rezystancja zastosowana samodzielnie prowadzi do niestabilności układu (wobec ujemnych wartości rezystancji bieguny układu znajdą się w prawej półpłaszczyźnie). Z tego względu stosuje się ją zwykle w specjalnych połączeniach z innymi elementami obwodowymi zapewniającymi stabilne działanie układu. Konwerter ujemno-impedancyjny jest łatwo realizowalny w technologii scalonej przy wykorzystaniu tranzystorów lub wzmacniaczy operacyjnych. Z tego względu jest chętnie wykorzystywany w elektronice przy realizacji filtrów, generatorów i innych układów przetwarzania sygnałów.

---

Zadanie 10.1

Wyznaczyć macierzowy opis czwórnikowy czwórnika typu $\mathrm{\Pi }$ o strukturze podanej na rysunku poniżej.

Rozwiązanie

Układ równań Kirchhoffa opisujących obwód

$I_1=Y_1{U}_1+I_3$

$I_2=Y_2{U}_2-I_3$

$I_3=Y_3(U_1-U_2)$

Równania czwórnikowe

$I_1=(Y_1+Y_3)U_1-Y_3{U}_2$

$I_2=-Y_3{U}_1+(Y_2+Y_3)U_2$

Macierz admitancyjna

$Y=\left[\begin{array}{cc}{Y}_1+Y_3& -Y_3\\ -Y_3& Y_2+Y_3\end{array}\right]$

Zadanie 10.2

Wyznaczyć macierz łańcuchową czwórnika odpowiadającego obwodowi z rysunku poniżej. Określić na tej podstawie transmitancję napięciową układu.

Rozwiązanie

Z równań Kirchhoffa dla obwodu otrzymuje się

$U_1=Z_1{I}_1+U_2=Z_1(k{I}_2-I_2+\frac{U_2}{Z_2})+U_2$

$I_1=k{I}_2-I_2+\frac{U_2}{Z_2}$

Opis łańcuchowy czwórnika

$\left[\begin{array}{c}{U}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}1+\frac{Z_1}{Z_2}& Z_1-k{Z}_1\\ \frac{1}{Z_2}& 1-k\end{array}\right]\left[\begin{array}{c}{U}_2\\ -I_2\end{array}\right]$

Transmitancja napięciowa określana przy założeniu $I_2=0$ jest równa

$T_u(s)=\frac{1}{A_{11}}=\frac{Z_2}{Z_1+Z_2}$