PEE Moduł 8: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 555: | Linia 555: | ||
: <math>\varphi=arctg \frac{\omega}{R/2L}</math> | : <math>\varphi=arctg \frac{\omega}{R/2L}</math> | ||
Napięcie na kondensatorze wyznaczyć można bezpośrednio z prawa napięciowego Kirchhoffa zastosowanego do obwodu rzeczywistego | Napięcie na kondensatorze wyznaczyć można bezpośrednio z prawa napięciowego Kirchhoffa zastosowanego do obwodu rzeczywistego. | ||
<math>u_C(t)=E-u_L(t)-Ri(t)=</math> | <math>u_C(t)=E-u_L(t)-Ri(t)=</math> | ||
| Linia 565: | Linia 565: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd29.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd29.png]] | ||
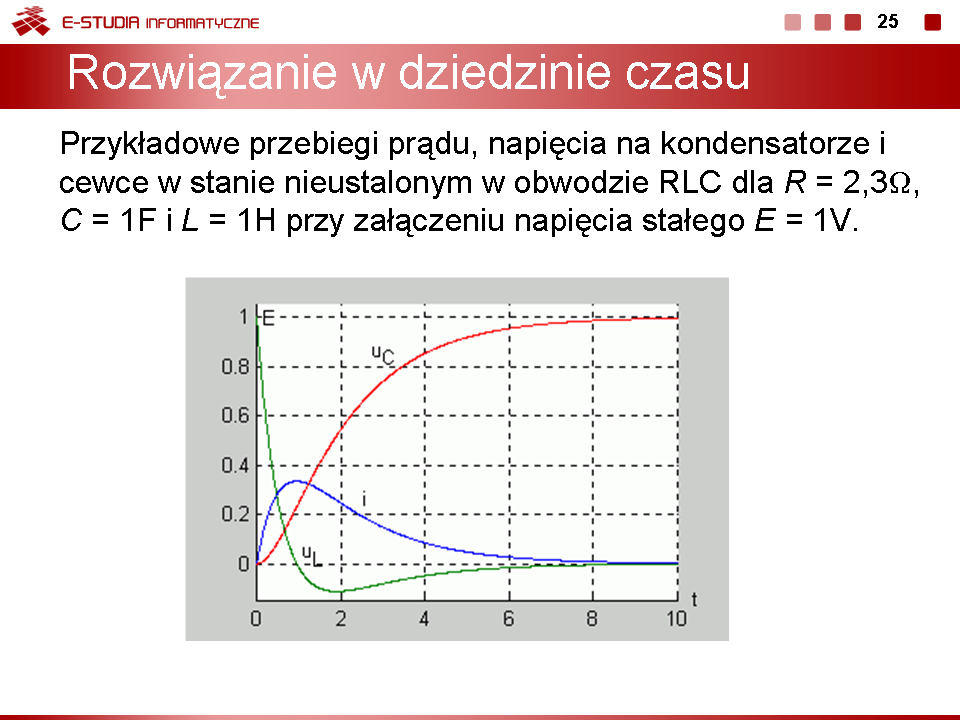
|valign="top"|Na slajdzie | |valign="top"|Na slajdzie obok przedstawiono przebiegi prądu i napięć w stanie nieustalonym w obwodzie RLC przy wystąpieniu przypadku oscylacyjnego, czyli przy <math>R<2\sqrt{\frac{L}{C}}</math>. | ||
Przebieg prądu ma charakter sinusoidalny, tłumiony wykładniczo do zera. Obwiednie przebiegu prądu są wyznaczone funkcjami <math>f(t)=\pm \frac{E}{\omega L}e^{-\frac{R}{2L}t}</math> . Przy zasilaniu obwodu RLC napięciem stałym wytworzyły się drgania własne o pulsacji <math>\omega=\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}</math>. Pulsacja ta zależy wyłącznie od parametrów obwodu RLC. Głównym czynnikiem regulującym wartość pulsacji wobec małej wartości rezystancji R dla przypadku oscylacyjnego jest wartość indukcyjności L oraz pojemności C. Przy danych wartościach L, C i regulowanej rezystancji, pulsacja rośnie przy malejącej wartości rezystancji. | Przebieg prądu ma charakter sinusoidalny, tłumiony wykładniczo do zera. Obwiednie przebiegu prądu są wyznaczone funkcjami <math>f(t)=\pm \frac{E}{\omega L}e^{-\frac{R}{2L}t}</math> . Przy zasilaniu obwodu RLC napięciem stałym wytworzyły się drgania własne o pulsacji <math>\omega=\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}</math>. Pulsacja ta zależy wyłącznie od parametrów obwodu RLC. Głównym czynnikiem regulującym wartość pulsacji wobec małej wartości rezystancji R dla przypadku oscylacyjnego jest wartość indukcyjności L oraz pojemności C. Przy danych wartościach L, C i regulowanej rezystancji, pulsacja rośnie przy malejącej wartości rezystancji. | ||
|} | |} | ||
| Linia 577: | Linia 576: | ||
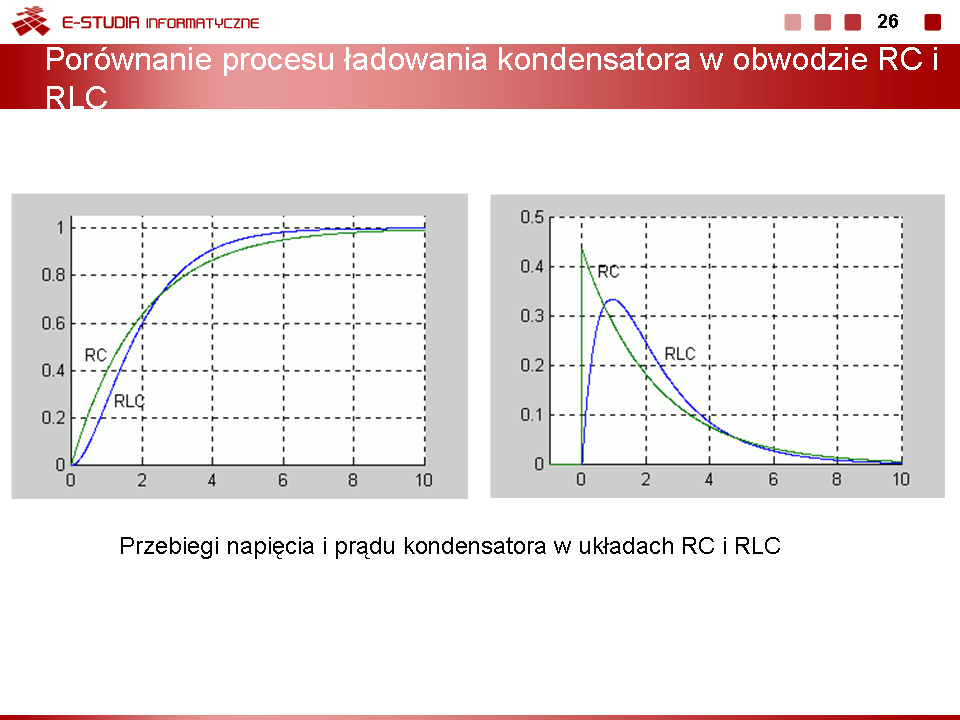
|valign="top"|Drgania w obwodzie powstają na skutek wymiany energii między polem elektrycznym kondensatora a polem magnetycznym cewki. Na skutek skończonej wartości rezystancji zachodzi rozpraszanie energii w postaci ciepła wydzielanego na rezystorze. Stąd oscylacje powstające w obwodzie mają charakter malejący. Szybkość tłumienia określa stała tłumienia <math>\alpha=\frac{R}{2L}</math>. Im większa wartość rezystancji tym większe tłumienie w obwodzie i szybsze zanikanie drgań sinusoidalnych do zera. | |valign="top"|Drgania w obwodzie powstają na skutek wymiany energii między polem elektrycznym kondensatora a polem magnetycznym cewki. Na skutek skończonej wartości rezystancji zachodzi rozpraszanie energii w postaci ciepła wydzielanego na rezystorze. Stąd oscylacje powstające w obwodzie mają charakter malejący. Szybkość tłumienia określa stała tłumienia <math>\alpha=\frac{R}{2L}</math>. Im większa wartość rezystancji tym większe tłumienie w obwodzie i szybsze zanikanie drgań sinusoidalnych do zera. | ||
Animacja i rysunek na slajdzie przedstawiają przykładowe przebiegi ładowania kondensatora w obwodzie RLC dla przypadków oscylacyjnych przy zmieniającej się wartości rezystancji. | |||
Widoczne jest, że im mniejsza wartość rezystancji tym dłużej trwa stan przejściowy w obwodzie. Wobec małych wartości rezystancji wynikających z warunku występowania przypadku oscylacyjnego jej wpływ na częstotliwość drgań własnych obwodu jest stosunkowo niewielki. | |||
|} | |} | ||
| Linia 586: | Linia 584: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd34.png]] | |||
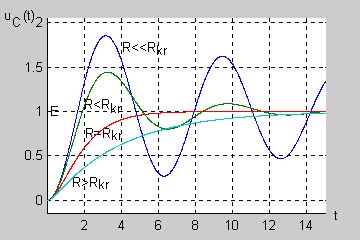
|valign="top"| | |valign="top"|Należy podkreślić, że jakkolwiek wyrażenia analityczne opisujące przebiegi czasowe w obwodzie dla różnych przypadków tłumienia są znacznie różniące się miedzy sobą, wszystkie reprezentują charakter ciągły. Poszczególne przypadki przechodzą w siebie nawzajem przy ciągłej zmianie wartości rezystancji. Przy małej rezystancji tłumienie jest małe i przebieg prądu oraz napięć jest oscylacyjny, tłumiony wykładniczo. Wzrost wartości rezystancji powoduje wzrost tłumienia, drgania trwają krócej aż przy pewnej wartości krytycznej <math>R_{kr}=2\sqrt{\frac{L}{C}}</math> przechodzą w przebieg aperiodyczny (krytyczny), przy którym nie obserwuje się już drgań. Dalszy wzrost rezystancji niewiele zmienia w charakterze jakościowym przebiegów poza wydłużeniem stanu przejściowego. Ilustrację powyższego zjawiska na przykładzie napięcia w obwodzie przedstawiono na rys. poniższym | ||
Należy podkreślić, że jakkolwiek wyrażenia analityczne opisujące przebiegi czasowe w obwodzie dla różnych przypadków tłumienia są znacznie różniące się miedzy sobą, wszystkie reprezentują charakter ciągły. Poszczególne przypadki przechodzą w siebie nawzajem przy ciągłej zmianie wartości rezystancji. Przy małej rezystancji tłumienie jest małe i przebieg prądu oraz napięć jest oscylacyjny, tłumiony wykładniczo. Wzrost wartości rezystancji powoduje wzrost tłumienia, drgania trwają krócej aż przy pewnej wartości krytycznej <math>R_{kr}=2\sqrt{\frac{L}{C}}</math> przechodzą w przebieg aperiodyczny (krytyczny), przy którym nie obserwuje się już drgań. Dalszy wzrost rezystancji niewiele zmienia w charakterze jakościowym przebiegów poza wydłużeniem stanu przejściowego. Ilustrację powyższego zjawiska na przykładzie napięcia w obwodzie przedstawiono na rys. poniższym | |||
{| | {| | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Rtxt1.jpg]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Rtxt1.jpg]] (animacja) | ||
|} | |} | ||
Wersja z 12:06, 25 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
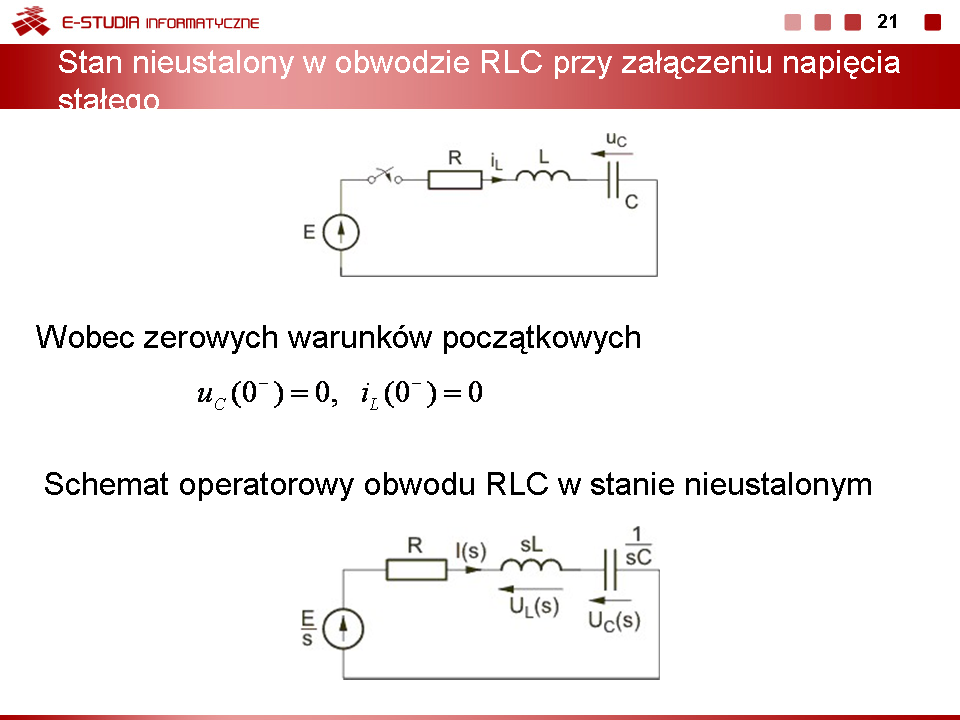
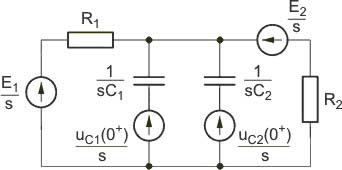
2) Stan ustalony po przełączeniu w obwodzie
|
|
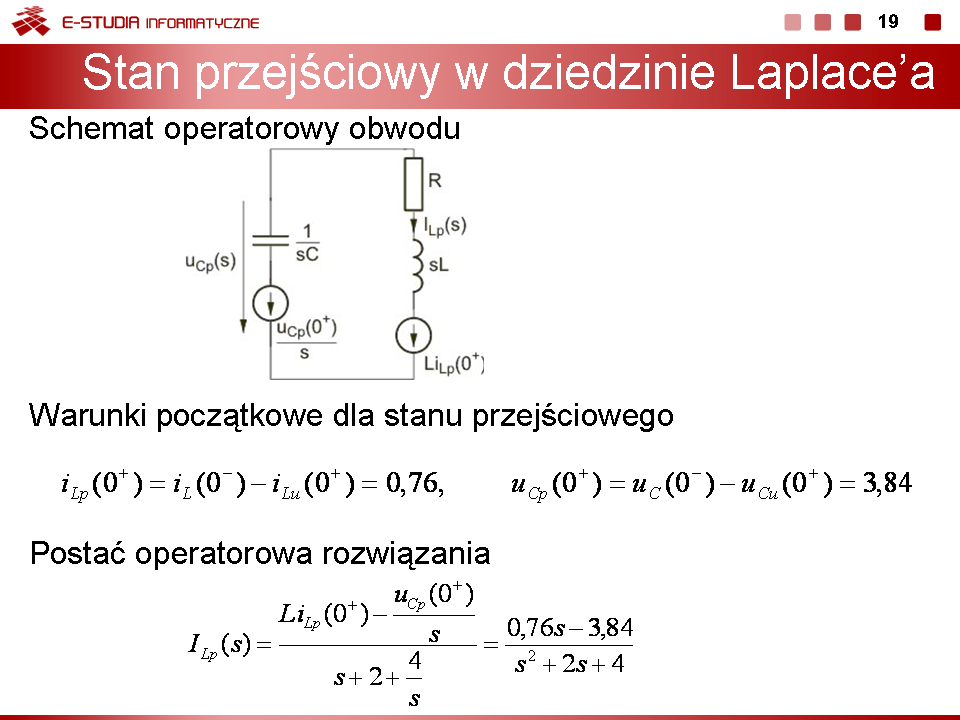
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rysunku obok.
Postać operatorowa rozwiązania |

|
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
|

|
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |
| Plik:PEE M8 Slajd34.png | Należy podkreślić, że jakkolwiek wyrażenia analityczne opisujące przebiegi czasowe w obwodzie dla różnych przypadków tłumienia są znacznie różniące się miedzy sobą, wszystkie reprezentują charakter ciągły. Poszczególne przypadki przechodzą w siebie nawzajem przy ciągłej zmianie wartości rezystancji. Przy małej rezystancji tłumienie jest małe i przebieg prądu oraz napięć jest oscylacyjny, tłumiony wykładniczo. Wzrost wartości rezystancji powoduje wzrost tłumienia, drgania trwają krócej aż przy pewnej wartości krytycznej przechodzą w przebieg aperiodyczny (krytyczny), przy którym nie obserwuje się już drgań. Dalszy wzrost rezystancji niewiele zmienia w charakterze jakościowym przebiegów poza wydłużeniem stanu przejściowego. Ilustrację powyższego zjawiska na przykładzie napięcia w obwodzie przedstawiono na rys. poniższym
Zadanie 8.1 Wyznaczyć transformatę odwrotną Laplace’a dla transmitancji operatorowej F(s)
W rozważanym przypadku wszystkie bieguny są rzeczywiste, przy czym jeden z nich jest podwójny. Ich wartości są równe: , , . Najskuteczniejszą metodą pozostaje w tym przypadku metoda residuów, zgodnie z którą
Określić przebieg napięcia na kondensatorze w stanie nieustalonym po przełączeniu metodą operatorową w obwodzie przedstawionym na rys. poniższym. Przyjąć następujące parametry obwodu:, , , , , .
Warunki początkowe: , Ze względu na wymuszenie stałe nie zachodzi potrzeba stosowania metody superpozycji stanu. Schemat operatorowy obwodu w stanie nieustalonym przedstawiony jest na rys. poniższym
Z metody potencjałów węzłowych zastosowanych do obwodu z rys. 9.18 wynika
Transformata odwrotna Laplace’a
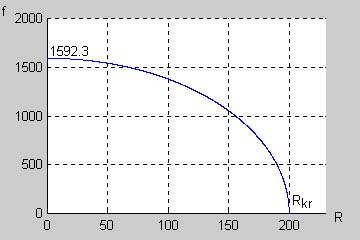
Wartości indukcyjności i pojemności w obwodzie szeregowym RLC są równe: oraz . Określić zmiany częstotliwości drgań własnych tego obwodu w funkcji wartości rezystancji R zmieniającej się od zera do rezystancji krytycznej.
Częstotliwość drgań własnych obwodu szeregowego RLC dana jest wzorem
|