PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 238: | Linia 238: | ||
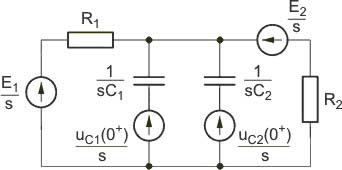
W modelu tym funkcja <math>Z_C= \frac{1}{sC}</math> reprezentuje impedancję operatorową kondensatora a <math>\frac{u_C(0^{+})}{s}</math> - źródło napięciowe stanowiące integralną część modelu. | W modelu tym funkcja <math>Z_C= \frac{1}{sC}</math> reprezentuje impedancję operatorową kondensatora a <math>\frac{u_C(0^{+})}{s}</math> - źródło napięciowe stanowiące integralną część modelu. | ||
Modele operatorowe odpowiadające podstawowym elementom obwodu pozwalają przyporządkować każdemu obwodowi rzeczywistemu jego schemat zastępczy w dziedzinie transformat. W schemacie tym niezerowe warunki początkowe uwzględnione są poprzez dodatkowe źródła napięcia występujące w modelu operatorowym cewki i kondensatora | Modele operatorowe odpowiadające podstawowym elementom obwodu pozwalają przyporządkować każdemu obwodowi rzeczywistemu jego schemat zastępczy w dziedzinie transformat. W schemacie tym niezerowe warunki początkowe uwzględnione są poprzez dodatkowe źródła napięcia występujące w modelu operatorowym cewki i kondensatora. | ||
|} | |} | ||
| Linia 245: | Linia 245: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd11.png]] | ||
|valign="top"| | |valign="top"|Dla schematu operatorowego obwodu słuszne są prawa Kirchhoffa, analogiczne do praw obowiązujących w dziedzinie czasu. | ||
Dla schematu operatorowego obwodu słuszne są prawa Kirchhoffa, analogiczne do praw obowiązujących w dziedzinie czasu. | |||
''Prawo prądowe'' | ''Prawo prądowe'' | ||
Suma transformat prądów w dowolnym węźle obwodu elektrycznego jest równa zeru | Suma transformat prądów w dowolnym węźle obwodu elektrycznego jest równa zeru | ||
: <math>\sum_{k=1}^n {I_k(s)=0}</math> | : <math>\sum_{k=1}^n {I_k(s)=0}</math> | ||
''Prawo napięciowe'' | ''Prawo napięciowe'' | ||
Suma transformat napięć gałęziowych w dowolnym oczku obwodu elektrycznego jest równa zeru | Suma transformat napięć gałęziowych w dowolnym oczku obwodu elektrycznego jest równa zeru | ||
: <math>\sum_{k=1}^n {U_k(s)=0}</math> | : <math>\sum_{k=1}^n {U_k(s)=0}</math> | ||
W równaniach tych transformaty prądów i napięć zastąpiły wartości czasowe występujące w podstawowej wersji praw Kirchhoffa. | |||
W równaniach tych transformaty prądów i napięć zastąpiły wartości czasowe występujące w podstawowej wersji praw Kirchhoffa. | |||
|} | |} | ||
| Linia 273: | Linia 266: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M8_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M8_Slajd12.png]] | ||
|valign="top"| | |valign="top"|Obliczenia prądów i napięć w stanie nieustalonym obwodu metodą operatorową sprowadzać się będą do wyznaczenia transformaty odpowiedniej wielkości a następnie obliczenia transformaty odwrotnej Laplace’a dla określenia zmiennej w dziedzinie czasu. Do obliczenia transformat prądów i napięć można stosować wszystkie poznane dotąd metody analizy obwodów, w tym metodę równań Kirchhoffa, oczkową, potencjałów węzłowych, Thevenina i Nortona operujące transformatami Laplace’a zamiast wartościami zespolonymi czy wartościami w dziedzinie czasu (dla obwodu rezystancyjnego). | ||
Obliczenia prądów i napięć w stanie nieustalonym obwodu metodą operatorową sprowadzać się będą do wyznaczenia transformaty odpowiedniej wielkości a następnie obliczenia transformaty odwrotnej Laplace’a dla określenia zmiennej w dziedzinie czasu. Do obliczenia transformat prądów i napięć można stosować wszystkie poznane dotąd metody analizy obwodów, w tym metodę równań Kirchhoffa, oczkową, potencjałów węzłowych, Thevenina i Nortona operujące transformatami Laplace’a zamiast wartościami zespolonymi czy wartościami w dziedzinie czasu (dla obwodu rezystancyjnego). | |||
W ogólności rozwiązując stan nieustalony w obwodzie metodą operatorową należy wyróżnić kilka etapów. | W ogólności rozwiązując stan nieustalony w obwodzie metodą operatorową należy wyróżnić kilka etapów. | ||
| Linia 285: | Linia 273: | ||
2. Określenie rozwiązania obwodu w stanie ustalonym po przełączeniu przy zastosowaniu metody symbolicznej z wykorzystaniem dowolnej metody analizy. Wynikiem jest postać czasowa rozwiązania ustalonego prądów cewek <math>i_{Lu}(t)</math> i napięć kondensatorów <math>u_{Cu}(t)</math>. Przez założenie t=0 otrzymuje się wartości prądów i napięć w chwili początkowej, to jest <math>i_{Lu}(0^{+})</math> oraz <math>u_{Cu}(0^{+})</math>. | 2. Określenie rozwiązania obwodu w stanie ustalonym po przełączeniu przy zastosowaniu metody symbolicznej z wykorzystaniem dowolnej metody analizy. Wynikiem jest postać czasowa rozwiązania ustalonego prądów cewek <math>i_{Lu}(t)</math> i napięć kondensatorów <math>u_{Cu}(t)</math>. Przez założenie t=0 otrzymuje się wartości prądów i napięć w chwili początkowej, to jest <math>i_{Lu}(0^{+})</math> oraz <math>u_{Cu}(0^{+})</math>. | ||
3. | 3. Określenie rozwiązania obwodu w stanie przejściowym po przełączeniu przy zastosowaniu metody operatorowej. | ||
4. Rozwiązanie obwodu w stanie nieustalonym jest sumą składowej ustalonej oraz składowej przejściowej, to jest | |||
: <math>i_L(t)=i_{Lu}(t)+i_{Lp}(t)</math> | : <math>i_L(t)=i_{Lu}(t)+i_{Lp}(t)</math> | ||
| Linia 294: | Linia 282: | ||
: <math>u_C(t)=u_{Cu}(t)+u_{Cp}(t)</math> | : <math>u_C(t)=u_{Cu}(t)+u_{Cp}(t)</math> | ||
Składowa przejściowa zanika z czasem do zera i pozostaje jedynie składowa ustalona określająca przebieg wielkości w stanie ustalonym. Taka metodyka rozwiązania stanów nieustalonych przy zastosowaniu transformacji Laplace’a nosi nazwę metody '''superpozycji stanów''', gdyż rozdziela w sposób jawny stan ustalony od stanu przejściowego. Jest szczególnie zalecana przy wymuszeniach sinusoidalnych, choć obowiązuje również dla obwodów prądu stałego. | |||
Składowa przejściowa zanika z czasem do zera i pozostaje jedynie składowa ustalona określająca przebieg wielkości w stanie ustalonym. Taka metodyka rozwiązania stanów nieustalonych przy zastosowaniu transformacji Laplace’a nosi nazwę metody '''superpozycji stanów''', gdyż rozdziela w sposób jawny stan ustalony od stanu przejściowego. Jest szczególnie zalecana przy wymuszeniach sinusoidalnych, choć obowiązuje również dla obwodów prądu stałego | |||
|} | |} | ||
Wersja z 11:44, 25 sie 2006

|
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
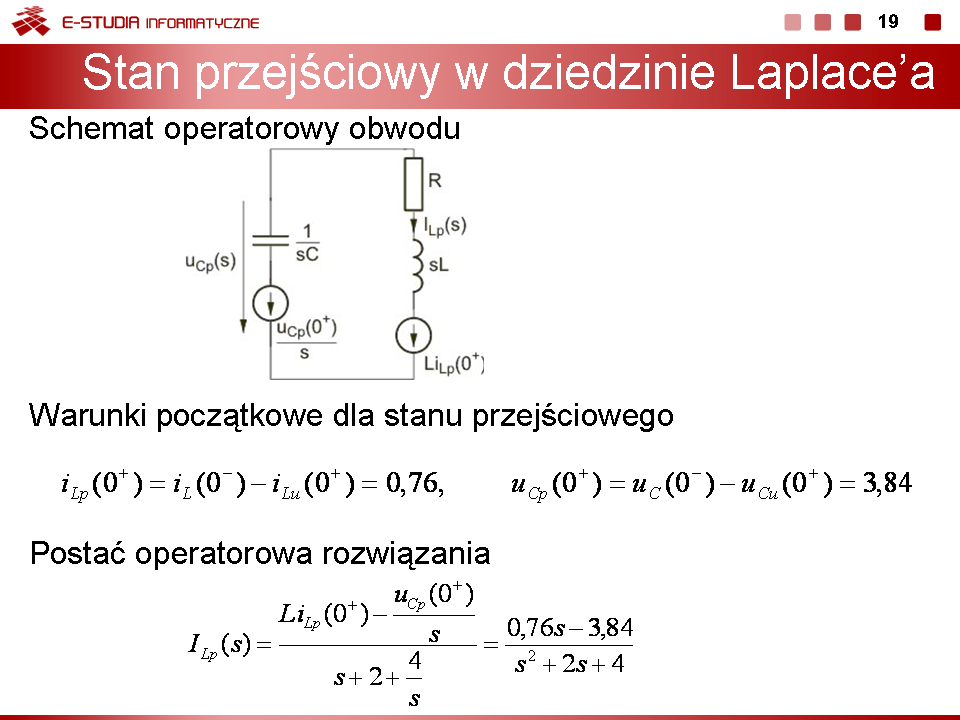
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
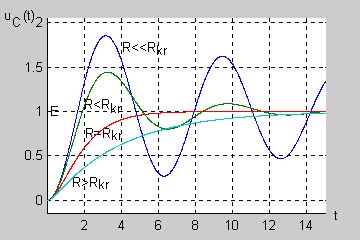
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |