PEE Moduł 8: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 187: | Linia 187: | ||
Prawo Ohma dotyczące wartości chwilowych prądu i napięcia dla rezystora można zapisać w postaci | Prawo Ohma dotyczące wartości chwilowych prądu i napięcia dla rezystora można zapisać w postaci | ||
: <math>u_R(t)=Ri_R(t)</math> | : <math>u_R(t)=Ri_R(t)</math> | ||
Jest to równanie algebraiczne wiążące prąd i napięcie na zaciskach elementu. Stosując transformację Laplace’a do obu stron równania otrzymuje się | Jest to równanie algebraiczne wiążące prąd i napięcie na zaciskach elementu. Stosując transformację Laplace’a do obu stron równania otrzymuje się | ||
: <math>U_R(s)=RI_R(s)</math> | : <math>U_R(s)=RI_R(s)</math> | ||
Jak wynika z powyższej zależności impedancja operatorowa dla rezystora jest równa samej rezystancji <math>Z_R(s)=R</math>. Rysunek na slajdzie obok przedstawia model operatorowy rezystora, obowiązujący w dziedzinie zmiennej zespolonej s. | |||
Jak wynika z powyższej zależności impedancja operatorowa dla rezystora jest równa samej rezystancji <math>Z_R(s)=R</math>. Rysunek | |||
|} | |} | ||
| Linia 209: | Linia 204: | ||
Dla uzyskania modelu operatorowego cewki idealnej zastosujemy przekształcenie Laplace’a bezpośrednio do równania opisującego cewkę w dziedzinie czasu | Dla uzyskania modelu operatorowego cewki idealnej zastosujemy przekształcenie Laplace’a bezpośrednio do równania opisującego cewkę w dziedzinie czasu | ||
: <math>u_L(t)=L \frac{di_L(t)}{dt}</math> | : <math>u_L(t)=L \frac{di_L(t)}{dt}</math> | ||
i wykorzystamy własność dotyczącą transformaty pochodnej. W efekcie otrzymuje się | i wykorzystamy własność dotyczącą transformaty pochodnej. W efekcie otrzymuje się | ||
: <math>U_L(s)=sLI_L(s)-Li_L(0^{+})</math> | : <math>U_L(s)=sLI_L(s)-Li_L(0^{+})</math> | ||
Powyższemu równaniu można przyporządkować schemat obwodowy cewki w dziedzinie operatorowej przedstawiony na rysunku obok. | |||
Powyższemu równaniu można przyporządkować schemat obwodowy cewki w dziedzinie operatorowej przedstawiony na rysunku | |||
Jest to połączenie szeregowe impedancji operatorowej odpowiadającej cewce idealnej i źródła napięciowego. Zaciski A-B modelu odpowiadają zaciskom A-B w oryginalnym symbolu cewki. Impedancja <math>Z_L(s)=sL</math> jest impedancją operatorową cewki a <math>Li_L(0^{+})</math> reprezentuje źródło napięcia stanowiące integralną część modelu. | Jest to połączenie szeregowe impedancji operatorowej odpowiadającej cewce idealnej i źródła napięciowego. Zaciski A-B modelu odpowiadają zaciskom A-B w oryginalnym symbolu cewki. Impedancja <math>Z_L(s)=sL</math> jest impedancją operatorową cewki a <math>Li_L(0^{+})</math> reprezentuje źródło napięcia stanowiące integralną część modelu. | ||
| Linia 232: | Linia 223: | ||
Dla uzyskania modelu operatorowego kondensatora idealnego skorzystamy z jego opisu w dziedzinie czasu | Dla uzyskania modelu operatorowego kondensatora idealnego skorzystamy z jego opisu w dziedzinie czasu | ||
: <math>i_C(t)=C \frac{du_C}{dt}</math> | : <math>i_C(t)=C \frac{du_C}{dt}</math> | ||
Zastosujemy przekształcenie Laplace’a do obu stron równania kondensatora. W efekcie takiej operacji otrzymuje się | Zastosujemy przekształcenie Laplace’a do obu stron równania kondensatora. W efekcie takiej operacji otrzymuje się | ||
: <math>I_C(s)=sCU_C(s)-Cu_C(0^{+})</math> | : <math>I_C(s)=sCU_C(s)-Cu_C(0^{+})</math> | ||
Przepiszemy tę zależność w postaci | Przepiszemy tę zależność w postaci | ||
: <math>U(s)=\frac{1}{sC}I_C(s)+ \frac{u_C(0^{+})}{s}</math> | : <math>U(s)=\frac{1}{sC}I_C(s)+ \frac{u_C(0^{+})}{s}</math> | ||
Równaniu powyższemu można przyporządkować schemat operatorowy kondensatora przedstawiony na rysunku obok. | |||
Równaniu powyższemu można przyporządkować schemat operatorowy kondensatora przedstawiony na rysunku | |||
W modelu tym funkcja <math>Z_C= \frac{1}{sC}</math> reprezentuje impedancję operatorową kondensatora a <math>\frac{u_C(0^{+})}{s}</math> - źródło napięciowe stanowiące integralną część modelu. | W modelu tym funkcja <math>Z_C= \frac{1}{sC}</math> reprezentuje impedancję operatorową kondensatora a <math>\frac{u_C(0^{+})}{s}</math> - źródło napięciowe stanowiące integralną część modelu. | ||
Wersja z 11:40, 25 sie 2006

|
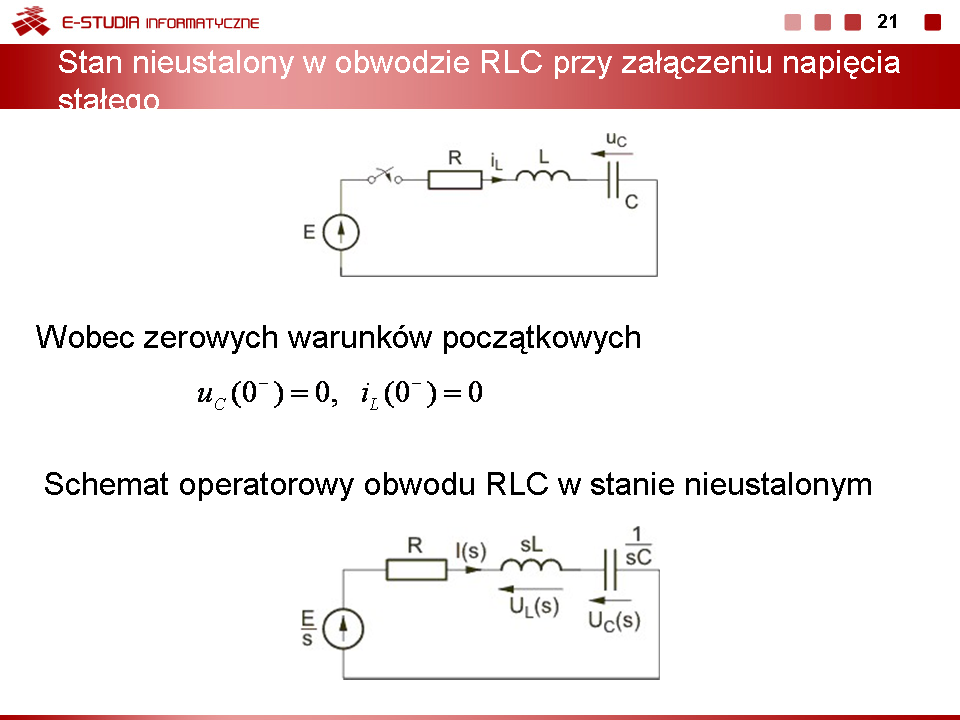
Wykład 8. Zastosowanie metody operatorowej Laplace’a w analizie stanów nieustalonych |

|
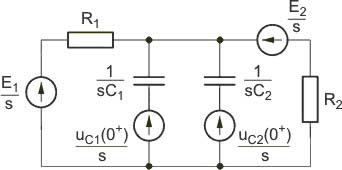
2) Stan ustalony po przełączeniu w obwodzie
(slajd 15) |
|
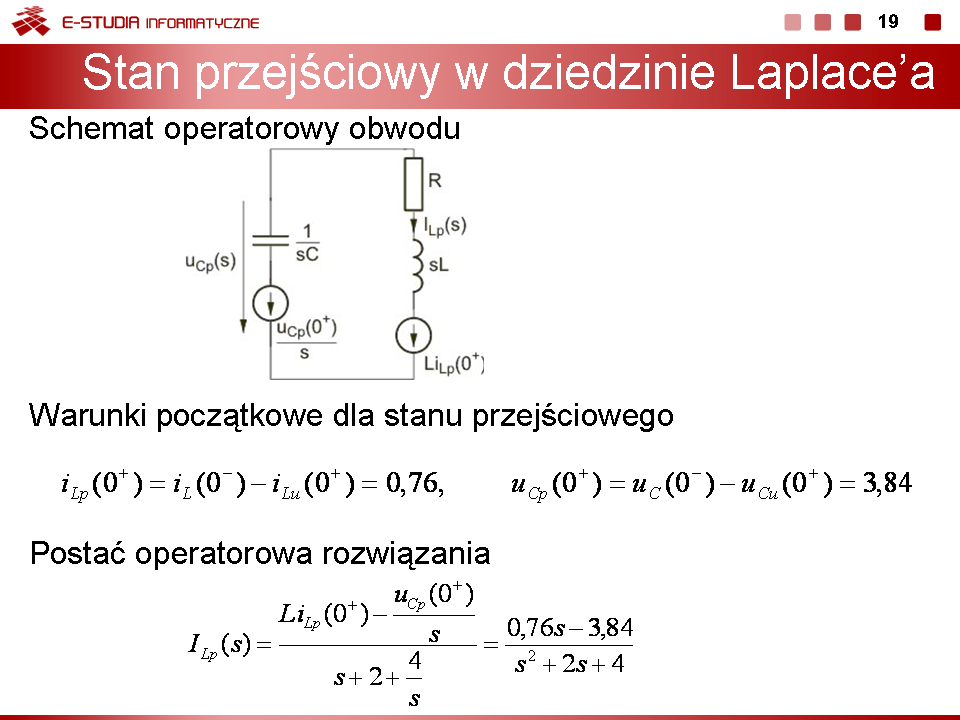
3) Stan przejściowy po przełączeniu
Schemat operatorowy przedstawiony jest na rys. na slajdzie 16 Warunki początkowe dla stanu przejściowego: |

|
Postać operatorowa rozwiązania
Wobec zespolonych biegunów zastosujemy metodę tablicową określenia transformaty odwrotnej. Zgodnie z nią
Rozwiązanie całkowite na prąd cewki w stanie nieustalonym
|

|
Przypadek aperiodyczny krytyczny
W przypadku aperiodycznym krytycznym, wobec spełnienia relacji oba pierwiastki mianownika są równe i transformata prądu wyraża się wzorem |