PF Moduł 8

Wprowadzenie Omówione są tu ogólne prawa makroskopowe opisujące prawidłowo zjawiska cieplne i pozwalające ilościowo przewidywać skutki różnych procesów.

---

Oznaczamy przez $\mathrm{\Delta }U$ zmianę energii wewnętrznej układu, który przechodzi ze stanu o energii wewnętrznej $U_1$ do stanu o energii wewnętrznej $U_2$. Zmiana ta może zachodzić na kilka sposobów: przez wykonanie pracy W nad układem lub przez układ nad otoczeniem, przez wymianę ciepła Q między układem i otoczeniem, przez wymianę materii M pomiędzy układem, a otoczeniem. Zapiszemy to następująco $\mathrm{\Delta }U=U_2-U_1=W+Q+M$ Wzór ten wyraża zasadę zachowania energii w procesach termodynamicznych i nosi nazwę pierwszej zasady termodynamiki. Zasada ta może, być sformułowana w następujący sposób: Przyrost energii wewnętrznej układu przy przejściu ze stanu początkowego do końcowego równy jest sumie dostarczonej do układu energii cieplnej, wykonanej nad układem pracy oraz energii uzyskanej wskutek wymiany materii z otoczeniem. Przyrost ten nie zależy od sposobu, w jaki dokonuje się przejście, a określony jest całkowicie przez początkowy i końcowy stan układu. Niemożliwe jest skonstruowanie silnika cyklicznego, który pracowałby bez pobierania z otoczenia energii. Taki hipotetyczny silnik nazwano perpetuum mobile I-go rodzaju. Niekiedy formułuje się pierwszą zasadę termodynamiki jako niemożliwość skonstruowania perpetuum mobile pierwszego rodzaju to jest skonstruowanie silnika cyklicznego, który pracowałby bez pobierania z otoczenia energii. Zaczerpnięty z łaciny zwrot "perpetuum mobile" znaczy "wiecznie poruszający się".

---

W ten sposób pierwsza zasada termodynamiki wskazuje na trzy różne sposoby zmiany energii wewnętrznej układu: na drodze wykonywania pracy nad układem bądź przez układ oraz poprzez wymianę ciepła lub/i materii pomiędzy układem a otoczeniem.

---

W naszych dalszych rozważaniach będziemy omawiać układy nie wymieniające materii z otoczeniem, dla których M=0. Zmiana energii wewnętrznej $\mathrm{\Delta }U$ układu o stałej masie dokonuje się poprzez wymianę ciepła $Q$, co zachodzi w warunkach różnicy temperatur pomiędzy układem i otoczeniem, lub/i poprzez pracę $W$ wykonaną nad układem lub przez układ nad otoczeniem. $\mathrm{\Delta }Q=Q+W$. Wprowadzamy tu konwencję, którą będziemy stosować w dalszych rozważaniach dla układów nie wymieniających materii z otoczeniem. Praca $W$ jest dodatnia $(W>0)$, jeżeli jest wykonywana przez siły zewnętrzne (otoczenie) nad układem fizycznym. Kiedy układ fizyczny wykonuje pracę nad otoczeniem (kosztem swej energii wewnętrznej) praca ta jest ujemna $(W<0)$. Podobnie, ciepło jest dodatnie $(Q>0)$, jeśli przepływa z otoczenia do układu, a ujemne $(Q<0)$, jeśli przepływa z układu do otoczenia. Dla przykładu, kiedy siły zewnętrzne (otoczenie) wykonują pracę sprężając gaz $(\mathrm{\Delta }V<0)$, to wykonana praca jest dodatnia, kiedy gaz wykonuje pracę nad otoczeniem rozprężając się $(\mathrm{\Delta }V>0)$, praca jest ujemna.

---

Dla wyznaczenia skończonej pracy wykonanej w procesie kwazistatycznym, odwracalnym, można rozpatrywać przemianę jako ciąg procesów elementarnych, w których zmiany parametrów układu są nieskończenie małe. Dla procesu elementarnego zapiszemy pierwsza zasadę termodynamiki w postaci $dU=\delta Q+\delta W$ UWAGA: Symbolami $\delta Q$ i $\delta W$ oznaczamy różniczkowe porcje (a nie skończone przyrosty) wymienianego przez układ ciepła i wykonanej pracy przy nieskończenie małych (infinitezymalnych) zmianach parametrów stanu układu. Wynika, to z faktu, ze ciepło i praca nie są funkcjami stanu, bowiem jak zobaczymy, zależą od drogi przejścia pomiędzy stanami. Mówimy, że są funkcjami procesu. Symbol $dU$ oznacza zmianę energii wewnętrznej, która jest funkcją stanu. W przemianie kołowej, kiedy układ powraca do stanu początkowego, jego energia wewnętrzna mieć będzie taką samą wartość jak w stanie początkowym, co zapisujemy w postaci $\oint dU=0$ Nieskończenie mały przyrost, dla którego spełniony jest powyższy warunek nazywamy różniczką zupełną. Kiedy warunek ten nie jest spełniony, mamy do czynienia z wyrażeniem różniczkowym. Różniczkami zupełnymi są nieskończenie małe przyrosty funkcji stanu, ale nie są nimi infinitezymalne ilości wymienianego ciepła, lub wykonanej pracy. Bilans ilości ciepła pobranego i oddanego przez układ w przemianie kołowej lub wykonanej przez układ pracy nie musi być równy zeru.

---

Przemiana izochoryczna to proces, w którym objętość układu pozostaje stała, czyli $V=const$. W przemianie tej nie jest wykonywana praca. W oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację $\delta Q_v=du$, co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła. Pojemność cieplna jednego mola, tzw. ciepło molowe substancji w procesie przebiegającym bez zmiany objętości wyraża się wzorem $C_v=(\frac{\partial U}{\partial T}{)}_v$, gdzie indeks v przy znaku pochodnej cząstkowej oznacza, że proces zachodzi w stałej objętości. Energia wewnętrzna danej masy gazu doskonałego zależy jednak wyłącznie od temperatury. Przekonuje nas o tym doświadczenie J.P. Joule'a z rozprężaniem rozrzedzonego gazu do próżni, gdy układ jest w osłonie izolacyjnej uniemożliwiającej wymianę ciepła z otoczeniem. Możemy wiec dla gazu doskonałego napisać, że $C_v=\frac{dU}{dT}$. W dowolnym procesie kwazistatycznym, odwracalnym, niezależnie, która z wielkości jest stała zmiana energii wewnętrznej $n_M$ moli gazu doskonałego jest określona wzorem: $dU=n_M\cdot C_v\cdot dT$. Bardziej szczegółowe uzasadnienie tego wzoru, w oparciu o analizę doświadczenia Joule'a, można znaleźć w literaturze. Zapamiętajmy, że powyższy wzór, określający zmianę energii wewnętrznej, ma charakter uniwersalny. Mimo że został sformułowany dla przypadku przemiany izochorycznej i występuje w nim ciepło molowe $C_v$, może być stosowany przy opisie innych przemian gazowych, gdyż energia wewnętrzna jest funkcją stanu. Informacja ta jest bardzo użyteczna przy rozwiązywaniu zadań.

---

Jeśli proces zachodzi pod stałym ciśnieniem, czyli $p=const$, to mówimy, że zachodzi przemiana izobaryczna. Z równania stanu wynika, że w tym przypadku objętość jest liniową funkcją temperatury. Przy wzroście objętości praca jest wykonywana przez gaz $(W<0,W^{\prime }>0)$, a przy zmniejszeniu objętości, przez otoczenie, $(W>0,W^{\prime }<0)$ Ciśnienie zachowuje stałą wartość, więc praca wykonana nad układem w przemianie izobarycznej wynosi $W=-\underset{V_1}{\overset{V_2}{\int }}p\cdot dV=-p\cdot \underset{V_1}{\overset{V_2}{\int }}dV=p\cdot (V_1-V_2)$. Podwyższenie temperatury o jeden kelwin wymaga więcej ciepła niż w przypadku ogrzewania bez zmiany objętości, bowiem część ciepła zużywana jest na wykonanie pracy. W procesie izobarycznym energię wewnętrzną możemy zmienić zarówno na drodze wykonania pracy jak i wymiany ciepła $dU=\delta Q_p-p\cdot dV$. Wyrażenie to możemy przepisać dla $n_M$ moli w innej postaci wykorzystując poznane wzory: $n_M\cdot C_v\cdot dT=n_M\cdot C_p\cdot dT-p\cdot dV$ gdzie wprowadziliśmy pojęcie ciepła molowego przy stałym ciśnieniu $C_p=\frac{\delta Q_p}{dT}$. Różniczkując równanie stanu dla procesu izobarycznego, w którym $p=const$ mamy $p\cdot dV=n_M\cdot R\cdot dT$ Wykorzystując ten związek możemy napisać, że $n_M\cdot C_v\cdot dT=n_M\cdot C_p\cdot dT-n_M\cdot R\cdot dT$ skąd otrzymujemy równanie Mayera $C_p=C_v+R$. Stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości jest parametrem określającym rodzaj gazu i oznaczany jest zwykle symbolem $\kappa$ (kappa). $\kappa =\frac{C_p}{C_v}$. Wykorzystując równanie Mayera można ciepła molowe $C_p$ i $C_v$ wyrazić za pomocą współczynnika $\kappa$. $\kappa =\frac{C_v+R}{C_v}=1+\frac{R}{C_v}$ lub $C_v=\frac{R}{\kappa -1}$, $C_p=\frac{\kappa \cdot R}{\kappa -1}$. Ze związków tych widzimy, że $\kappa >1$.

---

Jeśli dany proces zachodzi w stałej temperaturze, czyli $T=const$, to mówimy, że zachodzi przemiana izotermiczna. Z równania stanu gazu wynika natychmiast, że w przemianie tej ciśnienie gazu jest odwrotnie proporcjonalne do jego objętości, bowiem dla danej masy gazu wyrażonej w molach mamy $p\cdot V=n_M\cdot R\cdot T$, czyli $p=\frac{const}{V}$. Związek ten zwany jest prawem Boyle'a Mariotte'a. Pracę wykonaną nad układem przy przemianie izotermicznej wyznaczamy z jej definicji oraz korzystając z równania stanu dla przemiany izotermicznej. $W=-\underset{V_1}{\overset{V_2}{\int }}p\cdot dV=-n_M\cdot R\cdot T\cdot \underset{V_1}{\overset{V_2}{\int }}\frac{dV}{V}=$ $-n_M\cdot R\cdot T(ln{V}_2-ln{V}_1)=n_M\cdot R\cdot T\cdot ln(\frac{V_1}{V_2})$ Zapiszmy pierwsza zasadę termodynamiki dla przemiany izotermicznej w postaci różniczkowej, $dU=\delta Q_T-p\cdot dV$. W przemianie izotermicznej $T=const$, więc $dU=0$. Oznacza to, że w przemianie izotermicznej energia wewnętrzna układu nie zmienia się. Widzimy dalej, że temperatura układu jest stała, ale jest wymieniane ciepło między układem i otoczeniem. Ilość tego ciepła możemy określić $0=\delta Q_T-p\cdot dV$, czyli $\delta Q_T=p\cdot dV$. Wymiana ciepła następuje, na skutek wykonanej pracy. Jeśli praca jest wykonywana nad układem $(\delta W>0)$, to ciepło w równej ilości musi być oddawane do otoczenia $(\delta Q<0)$ i vice versa.

---

Przemiana, która zachodzi bez wymiany ciepła z otoczeniem - to przemiana adiabatyczna. Dla przemiany tej mamy $\delta Q=0$. W takim przypadku pierwsza zasada termodynamiki przyjmie postać $dU=-p\cdot dV$, co oznacza, że w przemianie tej energię wewnętrzną można zmienić jedynie poprzez wykonanie pracy. Zapiszmy to bardziej szczegółowo $dU=-p\cdot dV$, czyli $n_M\cdot C_v\cdot dT+\frac{n_M\cdot R\cdot T}{V}\cdot dV=0$. Można to zapisać nieco inaczej dzieląc obustronnie ostatnie równanie przez $n_M\cdot C_v\cdot T$ $\frac{dT}{T}+\frac{R}{C_v}\cdot \frac{dV}{V}=0$. Pamiętając z matematyki, że $d(lnx)=dx/x$ oraz, że różniczka sumy równa jest sumie różniczek, możemy to równanie przepisać w postaci $d(lnT+\frac{R}{C_v}\cdot lnV)=0$. Jeśli różniczka funkcji równa jest zeru, to funkcja równa jest stałej, czyli $lnT+\frac{R}{C_v}\cdot lnV=const$. Pamiętając, że $R/C_v=\kappa -1$ mamy $lnT+(\kappa -1)\cdot lnV=const$, lub $ln(T\cdot V^{\kappa -1})=const$. Jeśli logarytm funkcji równy jest stałej, to i sama funkcja pozostaje stała. Możemy wiec napisać $T\cdot V^{\kappa -1}=const$. Wykorzystując równanie stanu gazu doskonałego pV = RT dostajemy $\frac{p\cdot V}{R}\cdot V^{\kappa -1}=const$ lub $\frac{p\cdot V^{\kappa }}{R}=const$. Powyższe wzory pozostaną w mocy, jeśli stałą gazową $R$ włączymy do stałej po prawej stronie. Otrzymamy wtedy $p\cdot V^{\kappa }=const$. Związek ten jest równaniem adiabaty i nosi nazwę równania Poissona. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej $p\cdot T^{\kappa /(1-\kappa )}=const,V\cdot T^{1/(\kappa -1)}=const$. Realizacja przemiany adiabatycznej jest trudna, gdyż wymaga idealnej izolacji cieplnej gazu od otoczenia. Warto jednak zauważyć, że gdy sprężanie lub rozprężanie gazu zachodzi bardzo szybko, to nawet mimo nie najlepszej izolacji cieplnej przemiana taka ma charakter bardzo zbliżony do przemiany adiabatycznej. Właściwość tę wykorzystuje się w pracy silników cieplnych.

---

Jeśli w czasie przemiany pojemność cieplna ciała pozostaje stała, czyli C=const, to mówimy, że zachodzi przemiana politropowa. Znajdźmy dla gazu doskonałego związek pomiędzy ciśnieniem i objętością w takiej przemianie, czyli równanie politropy. Zapiszmy pierwszą zasadę termodynamiki dla gazu doskonałego w postaci różniczkowej, wzór pamiętając przy tym, że $\delta Q=C\cdot dT$ oraz, że $dU=C_v\cdot dT$ $n_M\cdot C_v\cdot dT=n_M\cdot C\cdot dT-p\cdot dV$. Wzór ten można też zapisać inaczej $n_M\cdot (C-C_v)\cdot dT=p\cdot dV$ lub $dT=\frac{p\cdot dV}{n_M\cdot (C-C_v)}$. Wykorzystamy także równanie stanu gazu doskonałego, różniczkując je mamy $p\cdot dV\cdot +V\cdot dp=n_M\cdot R\cdot dT$. Teraz wstawiając wyrażenie na $dT$ do ostatniego równania otrzymujemy po prostych przekształceniach $(C-C_v-R)\cdot p\cdot dV+(C-C_v)\cdot V\cdot dp=0$. Pamiętając, że $C_v+R=C_p$ i dzieląc stronami równanie przez $p\cdot V$ otrzymujemy równanie różniczkowe, w którym zauważamy wyrażenia będące różniczkami logarytmu $(C-C_p)\cdot \frac{dV}{V}+(C-C_v)\cdot \frac{dp}{p}=0$. Całkowanie tego równania daje w wyniku $(C-C_p)\cdot lnV+(C-C_v)\cdot lnp=const$. Dzieląc obie strony tego równania przez $(C-C_v)$, co jest możliwe tylko, jeżeli $(C\ne C_v)$, otrzymujemy po skorzystaniu z własności wyrażeń logarytmicznych $p\cdot V^n=const$. Powyższy wzór jest równaniem politropy gazu doskonałego obejmującym przypadki, dla których $(C\ne C_v)$. Wyrażenie $n=\frac{C-C_p}{C-C_v}$, nazywa się wykładnikiem politropy. (Pamiętajmy by nie mylić tego oznaczenia z oznaczeniem, także literą "n", liczby cząsteczek w jednostce objętości. Nie wprowadzamy tu nowych oznaczeń, by pozostać w zgodności z ogólnie przyjętym nazewnictwem.) Można teraz obliczyć ciepło molowe C w zależności od wykładnika n $C=\frac{n\cdot C_v-C_p}{n-1}$. Kiedy zaś $(C=C_v)$ to otrzymujemy, że $(C-C_p)\cdot lnV=const$. Przemiana taka zachodzi przy stałej objętości; jest to przemiana izochoryczna. Widzimy, że w tym przypadku wykładnik politropy $n\to \mathrm{\infty }$. Kiedy $n=0$, to $p=const$. Mamy wtedy do czynienia z przemianą izobaryczną zachodzącą przy stałym ciśnieniu. Kiedy $n=1$, mamy równanie $p\cdot V=const$. Pamiętając o postaci równania stanu $p\cdot V=R\cdot T$ widzimy, że przypadek ten dotyczy przemiany izotermicznej. Kiedy $C=0$, to $n=C_p/C_v=\kappa$ i równanie takiej przemiany przyjmuje postać $p\cdot V^{\kappa }=const$. Zerowe ciepło właściwe przemiany oznacza, że układ nie pobiera i nie oddaje ciepła, $\delta Q=0$ pomimo zmiany temperatury, czyli nie wymienia ciepła z otoczeniem. Jest to przemiana adiabatyczna. Wszystkie opisane przemiany są faktycznie różnymi odmianami przemiany politropowej, czyli tworzą rodzinę przemian politropowych (bardziej po polsku - wielokierunkowych).

---

Pierwsza zasada termodynamiki nie wystarcza do pełnego opisu procesów zachodzących w przyrodzie. Dla przykładu, całkowicie zgodna z pierwszą zasadą termodynamiki byłaby zamiana na pracę nieprzebranej ilości energii cieplnej tkwiącej w wodach mórz i oceanów, w powietrzu, czy skorupie ziemskiej. Wiemy, że energia ta nie może być w całości zamieniona na pracę. Wymieńmy jeszcze inne przykłady procesów, które nie mogą zachodzić, chociaż nie są sprzeczne z zasadą zachowania energii. Wiemy, że wskutek tarcia wytwarzają się znaczne ilości ciepła. Pierwotni ludzie tak właśnie rozniecali ogień. Tarcie jest przyczyną rozgrzewania się hamulców w samochodach. Nie zdarza się jednak, by ciepło powstałe wskutek ruchu trących się przedmiotów wprawiło te przedmioty z powrotem w ruch. Gdy w naczyniu znajduje się powietrze pod ciśnieniem większym od ciśnienia atmosferycznego, to opuści ono naczynie, kiedy tylko pojawi się w nim otwór. Proces ten następuje samorzutnie aż do momentu wyrównania się ciśnień wewnątrz i na zewnątrz naczynia. Jest to jednak proces nieodwracalny, bowiem proces odwrotny jest nieprawdopodobny. Gdy stykają się dwa ciała o różnych temperaturach następuje przepływ ciepła od ciała o temperaturze wyższej do ciała o niższej temperaturze. Proces trwa aż do momentu wyrównania się temperatur. Nie obserwujemy nigdy samorzutnego przepływu ciepła od ciał chłodniejszych do cieplejszych. Istnieje szereg warunków zachodzenia procesów w przyrodzie - innych niż te, wynikające z zasady zachowania energii. Warunki te ujęte są w postaci drugiej zasady termodynamiki, która może być sformułowana na kilka sposobów. Sformułowanie podane przez Clausiusa w 1850r. Niemożliwe jest przekazywanie ciepła przez ciało o temperaturze niższej ciału o temperaturze wyższej bez wprowadzenia innych zmian w obu ciałach i w otoczeniu. Sformułowanie podane przez Kelvina w 1851r. Niemożliwe jest pobieranie ciepła z jednego termostatu i zamiana go w całości na pracę bez wprowadzania innych zmian w układzie i w otoczeniu. Właśnie sformułowanie Kelvina wskazuje na brak możliwości wykorzystania ciepła zmagazynowanego w wodzie oceanów. Hipotetyczny silnik, który pobierałby ciepło z otoczenia i zamieniał je w całości na pracę nazwano "perpetuum mobile drugiego rodzaju". Drugą zasadę termodynamiki sformułować można wiec także w następujący sposób. Skonstruowanie perpetuum mobile drugiego rodzaju jest niemożliwe

---

W silnikach (maszynach) cieplnych ciepło zamieniane jest na pracę. Elementami silnika są: źródło ciepła (grzejnik) o temperaturze $T_1$, chłodnica o temperaturze $T_2$ i substancja robocza, którą jest gaz. Pracę silnika charakteryzuje sprawność (wydajność). Sprawność silnika określa, jaka część energii pobranej na sposób ciepła może być przekazana innemu układowi na sposób pracy, w jednym cyklu. Dla wykonania pracy konieczne jest oddawanie części ciepła otoczeniu, a warunkiem tego jest chłodnica o niższej temperaturze niż temperatura źródła ciepła. Gdy zaś temperatury źródła i odbiornika ciepła stają się bliskie, to wydajność silnika zmniejsza się do zera. W silnikach cieplnych realizowany jest cykl przemian termodynamicznych. Oznacza to, że układ, który przemianom tym podlega, powraca cyklicznie do stanu początkowego. Nie oznacza to jednak, że cykl taki musi być odwracalny. Pamiętamy, że proces odwracalny to taki, który może przebiegać od stanu początkowego do końcowego i odwrotnie przechodząc przez ten sam ciąg procesów kwazistacjonarnych bez wprowadzania zmian w otoczeniu. Warunek ten nie jest nigdy spełniony w rzeczywistych silnikach cieplnych. Zanim jednak będziemy rozpatrywać pracę konkretnych typów silników zajmiemy się cyklem, który będzie wygodnym punktem odniesienia do dalszych naszych rozważań. Cykl ten rozpatrywany był przez francuskiego inżyniera i fizyka Leonarda Sadi Carnota na początku XIX-go wieku i zwany jest cyklem Carnota. Jest to cykl odwracalny składający się z dwóch przemian izotermicznych oraz dwóch adiabatycznych.

---

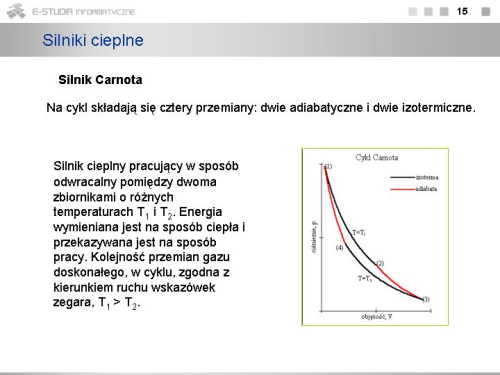
Silnik cieplny pracujący w sposób odwracalny pomiędzy dwoma zbiornikami o różnych temperaturach $T_1$ i $T_2$. Energia wymieniana jest na sposób ciepła i przekazywana jest na sposób pracy. Kolejność przemian gazu doskonałego, w cyklu, zgodna z kierunkiem ruchu wskazówek zegara, $T_1>T_2$. Na cykl składają się cztery przemiany: dwie adiabatyczne i dwie izotermiczne. Zakładamy, że cykl rozpoczyna się stanem (1) opisanym przez $p_1,V_1,T_1$ i odpowiednio poprzez kolejne stany (2), (3), (4) kończy powrotem do stanu (1).

---

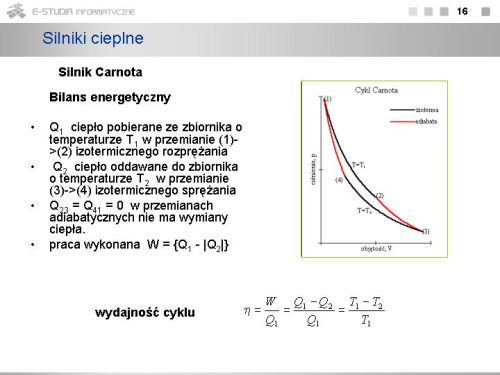
W przemianie (1)->(2) izotermicznego rozprężania gaz pobiera ciepło $Q_1$ ze zbiornika o temperaturze $T_1$. Przemiana zachodzi przy stałej temperaturze, więc energia wewnętrzna gazu nie ulega zmianie oraz $W{\text{'}}_1=Q_1=\underset{V_1}{\overset{V_2}{\int }}p\cdot dV=R\cdot T_1\cdot \underset{V_1}{\overset{V_2}{\int }}\frac{dV}{V}=R\cdot T_1\cdot ln\frac{V_2}{V_1}>0$. W przemianie drugiej, zachodzącej pomiędzy punktami 2 i 3, gaz ulega rozprężeniu adiabatycznemu. Oznacza to, że odcięty został zarówno dopływ ciepła, jak i możliwość przekazania ciepła otoczeniu, ale rozprężanie odbywało się nadal do objętości $V_3$. Trzeci etap jest znów przemianą izotermiczną, w której gaz zostaje sprężony od objętości $V_3$ do $V_4$. Gaz oddaje ciepło do chłodnicy o wielkiej pojemności cieplnej, wiec temperatura $T_2$ pozostaje niezmieniona, ale wskutek rozprężania adiabatycznego od objętości $V_2$ do $V_3$, które zaszło wcześniej, jest niższa od temperatury $T_1$. Praca wykonana przez gaz w tym procesie wynosi $W{\text{'}}_2=Q_2=\underset{V_3}{\overset{V_4}{\int }}p\cdot dV=R\cdot T_2\cdot \underset{V_3}{\overset{V_4}{\int }}\frac{dV}{V}=-R\cdot T_2\cdot ln\frac{V_3}{V_4}<0$. Zauważmy, że w tym przypadku obie wielkości: wykonana praca i ciepło "pobrane" z chłodnicy są ujemne. Ciepło oddane, któremu przypisujemy wartość dodatnią, oznacza się zwykle symbolem $\overline{Q}$. Mamy więc ${\overline{Q}}_2=-Q_2$. Czwarty proces jest znów adiabatyczny i przeprowadza układ od punktu 4 do początkowego punktu 1. W ten sposób cykl zostaje zamknięty, a energia wewnętrzna po wykonaniu całego cyklu ma swą pierwotną wartość. Przyrost energii wewnętrznej układu równy jest zeru, a sumaryczna wykonana praca równa jest pobranemu przez układ ciepłu $W^{\prime }=W{\text{'}}_1+W{\text{'}}_2=Q_1-{\overline{Q}}_2$. Stosunek pracy wykonanej przez układ w jednym cyklu do pobranego w tym cyklu ciepła nazywamy sprawnością lub wydajnością silnika cieplnego (maszyny cieplnej). W naszym przypadku mamy $\eta =\frac{W^{\prime }}{Q_1}=\frac{Q_1-{\overline{Q}}_2}{Q_1}=1-\frac{{\overline{Q}}_2}{Q_1}$. Widzimy, że sprawność byłaby równa jedności gdyby całe ciepło zostało zamienione na pracę. Układ musiałby wyłącznie pobierać ciepło. Część ciepła musi być jednak oddawana otoczeniu i w rezultacie sprawność jest zawsze mniejsza od jedności. Wykorzystując własności przemiany adiabatycznej, mamy w naszym przypadku związki $T_1\cdot V_2^{\kappa -1}=T_2\cdot V_2^{\kappa -1}$ oraz $T_1\cdot V_1^{\kappa -1}=T_2\cdot V_4^{\kappa -1}$. Dzieląc stronami pierwsze z powyższych równań przez drugie otrzymujemy $(\frac{V_2}{V_1}{)}^{\kappa -1}=(\frac{V_3}{V_4}{)}^{\kappa -1}$ czyli $\frac{V_2}{V_1}=\frac{V_3}{V_4}$. Wykorzystując ten związek mamy $\frac{{\overline{Q}}_2}{Q_1}=\frac{T_2}{T_1}$ lub $\frac{Q_1}{T_1}=\frac{{\overline{Q}}_2}{T_2}$. Wynika z tego, że sprawność silnika Carnota może być przedstawiona w postaci $\eta =1-\frac{T_2}{T_1}=\frac{T_1-T_2}{T_1}$. Otrzymaliśmy ważny związek, który mówi, że sprawność silnika Carnota określona jest wyłącznie stosunkiem temperatur; mniejszej do większej, i że rośnie wraz ze zmniejszaniem się tego stosunku. Widzimy też, że sprawność ta jest mniejsza od jedności, co oznacza, że nie całe pobrane ciepło zamienia się na pracę. Część ciepła oddawana jest chłodnicy, ale jest to konieczne dla przeprowadzenia cyklu kołowego. Jeśli cykl jest nieodwracalny, co może być wynikiem niedoskonałej izolacji cieplnej lub tego, że przemiany nie są kwazistatyczne, to sprawność silnika jest mniejsza niż w przypadku cyklu odwracalnego $\eta =1-\frac{{\overline{Q}}_2}{Q_1}<1-\frac{T_2}{T_1}$. Wniosek, że sprawność silnika Carnota zależy wyłącznie od stosunku temperatur znany jest pod nazwą pierwszego twierdzenia Carnota. Twierdzenia Carnota: 1. Wszystkie silniki pracujące w odwracalnym cyklu Carnota pomiędzy tymi samymi temperaturami mają tę samą sprawność. Twierdzenie to oznacza również, że sprawność dowolnego cyklu odwracalnego, ale składającego się z innych przemian niż cykl Carnota nie może być większa od sprawności odwracalnego cyklu Carnota. Drugie twierdzenie dotyczy sprawności silników nieodwracalnych. 2. Sprawność cyklu nieodwracalnego jest zawsze mniejsza od sprawności cyklu odwracalnego. Zwróćmy uwagę, że możliwe jest także przeprowadzenie cyklu w kierunku odwrotnym. Oznacza to, że nad układem wykonywana jest praca, zaś ciepło odbierane jest z chłodnicy i przekazywane nagrzewnicy. Układ taki działa jak maszyna chłodząca, czyli może stanowić lodówkę. Ciepło odbierane jest wtedy od ciała o temperaturze niższej i przekazywane ciału o temperaturze wyższej poprzez wykonanie pracy. Odpowiednikiem sprawności jest tutaj skuteczność chłodzenia określona jako $\xi =\frac{Q}{W^{\prime }}=\frac{{\overline{Q}}_2}{Q_1-{\overline{Q}}_2}$.

---

---

---

---

---

---