PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 37: | Linia 37: | ||
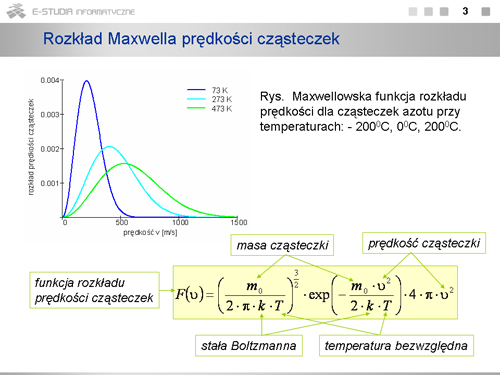
<math>F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | <math>F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | ||
Co jest charakterystyczne w tym rozkładzie <math>F(v)\,</math> ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od <math>v\,</math> . (Przeanalizuj dokładnie trzy człony wzoru na <math>F(v)\,</math> . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla | Co jest charakterystyczne w tym rozkładzie <math>F(v)\,</math> ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od <math>v\,</math> . (Przeanalizuj dokładnie trzy człony wzoru na <math>F(v)\,</math> . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla <math>v=0,\</math> , ostatni - rosnący paraboliczne ze wzrostem prędkości. Rezultat jest zobrazowany na wykresie maxwellowskiej funkcji rozkładu prędkości cząsteczek azotu przy temperaturach: <math>73 K\, (-200^\circ C)\,</math> , <math>273 K\, (0^\circ C)\,</math> , <math>473 K\, (200^\circ C)\,</math>. Gdy temperatura rośnie maksimum krzywej rozkładu przesuwa się w stronę większych prędkości i krzywa ulega spłaszczeniu. Pole pod krzywą równe jest całkowitej liczbie cząsteczek w próbce i pozostaje stałe niezależnie od temperatury. | ||
Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | ||
| Linia 51: | Linia 51: | ||
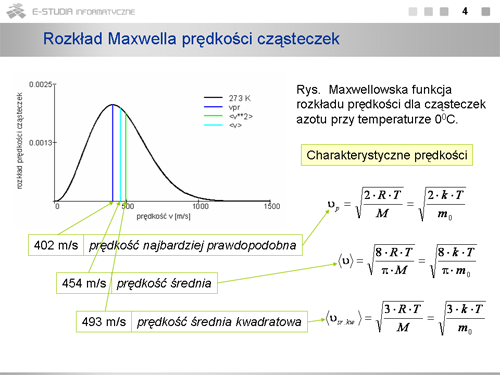
:<math>\frac{dF(v)}{dv}\Big|_{v=v_p}=0</math> | :<math>\frac{dF(v)}{dv}\Big|_{v=v_p}=0</math> | ||
Stąd otrzymuje się <math>v_p=\sqrt{2\cdot k\cdot T/m_0 }</math> , a więc <math>v_p<v_{ | Stąd otrzymuje się <math>v_p=\sqrt{2\cdot k\cdot T/m_0 }</math> , a więc <math>v_p<v_{sr. kw.}</math> jak to wynika z definicji średniej prędkości kwadratowej (teoria kinetyczna). | ||
Korzystając z funkcji rozkładu można obliczyć odpowiednio prędkość średnią (średnia arytmetyczną wszystkich prędkości) | Korzystając z funkcji rozkładu można obliczyć odpowiednio prędkość średnią (średnia arytmetyczną wszystkich prędkości) | ||
| Linia 67: | Linia 67: | ||
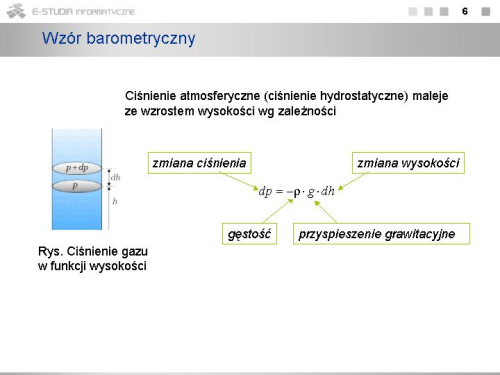
gdzie <math>\rho\,</math> jest gęstością gazu na wysokości <math>h\,</math> , a <math>g\,</math> jest przyspieszeniem ziemskim na tej wysokości. | gdzie <math>\rho\,</math> jest gęstością gazu na wysokości <math>h\,</math> , a <math>g\,</math> jest przyspieszeniem ziemskim na tej wysokości. | ||
Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola <math>p | Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola <math>p\cdot V=R\cdot T</math> przez wartość średniej masy molowej powietrza, określonej z uwzględnieniem procentowej zawartości azotu, tlenu i pozostałych gazów w powietrzu, otrzymujemy | ||
<math>p\cdot \begin{matrix} \underbrace{ (V/M) } \\ {1/{\rho}} \end{matrix}=\frac{R\cdot T}{M}</math> , czyli <math>\rho=\frac{M\cdot p}{R\cdot T}</math> | <math>p\cdot \begin{matrix} \underbrace{ (V/M) } \\ {1/{\rho}} \end{matrix}=\frac{R\cdot T}{M}</math> , czyli <math>\rho=\frac{M\cdot p}{R\cdot T}</math> | ||
| Linia 97: | Linia 97: | ||
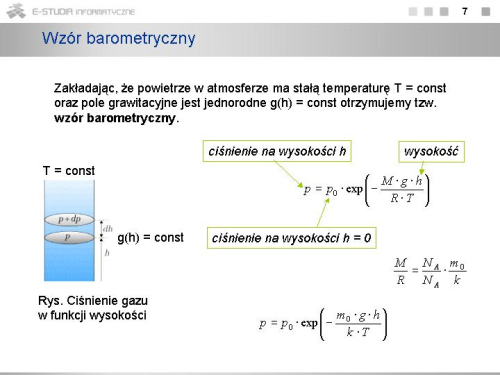
Wzór barometryczny obowiązuje dla '''atmosfery izotermicznej''', dla której mamy oraz jednorodnego pola grawitacyjnego. Jeżeli warunki te nie są spełnione, należy odpowiednio podstawić zależność funkcyjną temperatury od wysokości oraz zależność <math>g = g(h)\,</math> i rozwiązać otrzymane równanie różniczkowe. | Wzór barometryczny obowiązuje dla '''atmosfery izotermicznej''', dla której mamy oraz jednorodnego pola grawitacyjnego. Jeżeli warunki te nie są spełnione, należy odpowiednio podstawić zależność funkcyjną temperatury od wysokości oraz zależność <math>g = g(h)\,</math> i rozwiązać otrzymane równanie różniczkowe. | ||
Korzystając z faktu, że <math>\frac{ | Korzystając z faktu, że <math>\frac{M}{R}=\frac{N_A\cdot m_0}{N_A\cdot k}=\frac{m_0}{k}</math> , gdzie <math>m_0\,</math> - średnia masa cząsteczki powietrza, możemy wzór barometryczny przedstawić w postaci | ||
: <math>p=p_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{ | : <math>p=p_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{k\cdot T}\right)</math> | ||
|} | |} | ||
| Linia 111: | Linia 111: | ||
Przepiszmy w nieco innej formie wzór barometryczny. Zakładając atmosferę izotermiczną, możemy zamienić ciśnienia <math>p\,</math> i <math>p_0\,</math> występujące we wzorze barometrycznym wielkościami <math>n\,</math> i <math>n_0\,</math> , które reprezentują koncentrację cząsteczek, czyli ich liczbę w jednostce objętości na wysokości <math>h\,</math> oraz na powierzchni Ziemi. Wykorzystując to zapiszemy wzór barometryczny w formie | Przepiszmy w nieco innej formie wzór barometryczny. Zakładając atmosferę izotermiczną, możemy zamienić ciśnienia <math>p\,</math> i <math>p_0\,</math> występujące we wzorze barometrycznym wielkościami <math>n\,</math> i <math>n_0\,</math> , które reprezentują koncentrację cząsteczek, czyli ich liczbę w jednostce objętości na wysokości <math>h\,</math> oraz na powierzchni Ziemi. Wykorzystując to zapiszemy wzór barometryczny w formie | ||
: <math>n=n_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{ | : <math>n=n_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{k\cdot T}\right)</math> | ||
Zwróćmy uwagę, że wyrażenie <math>m_0\cdot g\cdot h\,</math> jest po prostu energią potencjalną <math>E_p\,</math> cząsteczki w polu sił ciężkości (przy założeniu jednorodnego pola grawitacyjnego). Więc również | Zwróćmy uwagę, że wyrażenie <math>m_0\cdot g\cdot h\,</math> jest po prostu energią potencjalną <math>E_p\,</math> cząsteczki w polu sił ciężkości (przy założeniu jednorodnego pola grawitacyjnego). Więc również | ||
: <math>n=n_0\cdot exp\left(-\frac{E_p}{ | : <math>n=n_0\cdot exp\left(-\frac{E_p}{k\cdot T}\right)</math> | ||
Ten wzór wyraża zależność koncentracji cząsteczek od ich wysokości lub grawitacyjnej energii potencjalnej. Wynikający z niego rozkład koncentracji nosi nazwę '''rozkładu Boltzmanna''' i odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. | Ten wzór wyraża zależność koncentracji cząsteczek od ich wysokości lub grawitacyjnej energii potencjalnej. Wynikający z niego rozkład koncentracji nosi nazwę '''rozkładu Boltzmanna''' i odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. | ||