PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 100: | Linia 100: | ||
: <math>p=p_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{R\cdot T}\right)</math> | : <math>p=p_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{R\cdot T}\right)</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
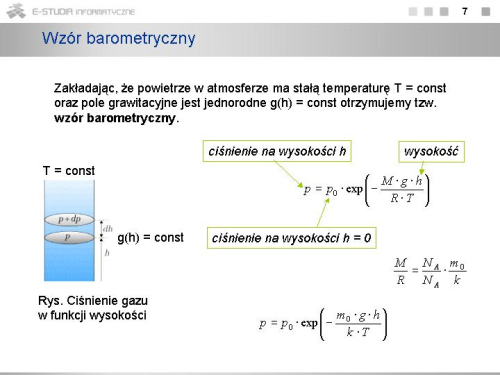
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd7.png]] | |||
|valign="top"|W rozważaniach dotyczących rozkładu Maxwella ignorowaliśmy całkowicie fakt, że cząsteczki poruszają się w polu sił ciężkości, a więc wyróżniony jest kierunek pionowy. Wzór barometryczny wskazuje, że ciężar cząsteczek ma wpływ na rozkład ciśnienia w funkcji wysokości. Jak uwzględnić ten efekt w opisie rozkładu prędkości cząsteczek? | |||
Przepiszmy w nieco innej formie wzór barometryczny. Zakładając atmosferę izotermiczną, możemy zamienić ciśnienia <math>p\,</math> i <math>p_0\,</math> występujące we wzorze barometrycznym wielkościami <math>n\,</math> i <math>n_0\,</math> , które reprezentują koncentrację cząsteczek, czyli ich liczbę w jednostce objętości na wysokości <math>h\,</math> oraz na powierzchni Ziemi. Wykorzystując to zapiszemy wzór barometryczny w formie | |||
: <math>n=n_0\cdot exp\left(-\frac{m_0 \cdot g\cdot h}{R\cdot T}\right)</math> | |||
Zwróćmy uwagę, że wyrażenie <math>m_0\cdot g\cdot h\,</math> jest po prostu energią potencjalną <math>E_p\,</math> cząsteczki w polu sił ciężkości (przy założeniu jednorodnego pola grawitacyjnego). Więc również | |||
: <math>n=n_0\cdot exp\left(-\frac{E_p}{R\cdot T}\right)</math> | |||
Ten wzór wyraża zależność koncentracji cząsteczek od ich wysokości lub grawitacyjnej energii potencjalnej. Wynikający z niego rozkład koncentracji nosi nazwę '''rozkładu Boltzmanna''' i odnosi się nie tylko do pola sił przyciągania ziemskiego, ale do dowolnego pola potencjalnego, jeśli tylko cząsteczki poruszają się chaotycznym ruchem cieplnym. | |||