PF Moduł 10

Wprowadzenie Termodynamika statystyczna opisuje układy wielu cząsteczek, z jakich składają się ciała za pomocą wielkości średnich (średnia prędkość, średnia droga, średnia energia itd.) oraz tzw. rozkładów statystycznych. Wiąże mikroskopowe, dane statystyczne o cząsteczkach z makroskopowymi parametrami stanu. Posługuje się rachunkiem prawdopodobieństwa i pozwala wyznaczać najbardziej prawdopodobne kierunki procesów.

---

Pomimo, że Identyczne cząsteczki są w chaotycznym ruchu Wszystkie kierunki ich ruchu są jednakowo prawdopodobne Temperatura jest miarą ich średniej energii kinetycznej Prędkości zmieniają się w wyniku zderzeń Prędkości poszczególnych cząsteczek są różne w szerokim zakresie wartości. To Rozkład Maxwella opisuje prędkości cząsteczek gazu doskonałego będącego w stanie równowagi termodynamicznej, na który nie działają siły zewnętrzne. Pozwala obliczyć charakterystyczne wartości wielkości średnich: średnią prędkość kwadratową, średnią prędkość i prędkość najbardziej prawdopodobną oraz liczbę cząsteczek o prędkościach zawartych w przedziale wartości od $v$ do $v+dv$. Jeżeli mamy $N$ cząsteczek, to liczba $d{N}_v$ cząsteczek o prędkościach w przedziale od $v$ do $v+dv$ będzie określona wzorem $d{N}_v=N\cdot F(v)\cdot dv$ , gdzie $F(v)$ dane jest wzorem $F(v)={\left(\frac{m_0}{2\cdot \pi \cdot k\cdot T}\right)}^{3/2}\cdot exp(-\frac{m_0\cdot v^2}{2\cdot k\cdot T})\cdot 4\cdot \pi \cdot v^2$

---

Wyprowadzenie wzoru można znaleźć w literaturze. $F(v)={\left(\frac{m_0}{2\cdot \pi \cdot k\cdot T}\right)}^{3/2}\cdot exp(-\frac{m_0\cdot v^2}{2\cdot k\cdot T})\cdot 4\cdot \pi \cdot v^2$ Co jest charakterystyczne w tym rozkładzie $F(v)$ ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od $v$ . (Przeanalizuj dokładnie trzy człony wzoru na $F(v)$ . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla , ostatni - rosnący paraboliczne ze wzrostem prędkości. Rezultat jest zobrazowany na wykresie maxwellowskiej funkcji rozkładu prędkości cząsteczek azotu przy temperaturach: $73K(-200^{\circ }C)$ , $273K(0^{\circ }C)$ , $473K(200^{\circ }C)$. Gdy temperatura rośnie maksimum krzywej rozkładu przesuwa się w stronę większych prędkości i krzywa ulega spłaszczeniu. Pole pod krzywą równe jest całkowitej liczbie cząsteczek w próbce i pozostaje stałe niezależnie od temperatury. Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach.

---

Dla każdej temperatury można określić prędkość, która występuje najczęściej, czyli najwięcej cząsteczek ma prędkości bliskie tej wartości. Wartość ta odpowiada maksimum rozkładu Maxwella. Prędkość tę nazywamy prędkością najbardziej prawdopodobną, $v_p$ . Można ją określić z matematycznego warunku na maksimum funkcji. $\frac{dF(v)}{dv}{|}_{v=v_p}=0$ Stąd otrzymuje się $v_p=\sqrt{2\cdot k\cdot T/m_0}$ , a więc Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_p<v_{śr. kw.}} jak to wynika z definicji średniej prędkości kwadratowej (teoria kinetyczna). Korzystając z funkcji rozkładu można obliczyć odpowiednio prędkość średnią (średnia arytmetyczną wszystkich prędkości)

---

Ciśnienie atmosferyczne w danym punkcie nad powierzchnią Ziemi określone jest przez ciężar warstwy powietrza leżącej powyżej tego punktu, powinno zależeć od wysokości. Im większa wysokość, tym mniejsza jest warstwa powietrza, więc i ciśnienie jest mniejsze. Różnica ciśnień $dp$ związana ze wzrostem wysokości $dh$ ma znak ujemny i wynosi $dp=-\rho \cdot g\cdot dh$ gdzie $\rho$ jest gęstością gazu na wysokości $h$ , a $g$ jest przyspieszeniem ziemskim na tej wysokości. Z dobrym przybliżeniem można potraktować powietrze jako gaz doskonały. Dzieląc obustronnie równanie stanu gazu doskonałego dla jednego mola $p|cdotV=R\cdot T$ przez wartość średniej masy molowej powietrza, określonej z uwzględnieniem procentowej zawartości azotu, tlenu i pozostałych gazów w powietrzu, otrzymujemy $p\cdot \begin{array}{c}\underbrace{(V/M)}\\ 1/\rho \end{array}=\frac{R\cdot T}{M}$ , czyli $\rho =\frac{M\cdot p}{R\cdot T}$ Więc możemy napisać, że $dp=-\frac{M\cdot p\cdot g}{R\cdot T}\cdot dh$ Otrzymujemy w ten sposób równanie różniczkowe o rozdzielonych zmiennych $\frac{dp}{p}=-\frac{M\cdot g}{R\cdot T}\cdot dh$ Zakładając, że temperatura atmosfery ma wartość stałą (tzw. atmosfera izotermiczna) i pole grawitacyjne jest jednorodne $(g(h)=const)$ możemy łatwo scałkować to równanie otrzymując $lnp=-\frac{M\cdot g\cdot h}{R\cdot T}+lnC$ gdzie $lnC$ to stała całkowania. Wynika stąd, że $p=C\cdot exp(-\frac{M\cdot g\cdot h}{R\cdot T})$ Dla $h=0$ ciśnienie równe jest ciśnieniu atmosferycznemu $p_0$ na powierzchni Ziemi. Stąd wyznaczamy stałą, $C=p_0$ . 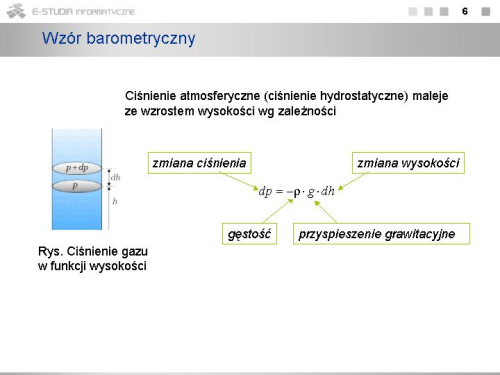Ostatecznie otrzymujemy $p=p_0\cdot exp(-\frac{M\cdot g\cdot h}{R\cdot T})$ Jest to tzw. wzór barometryczny. Wynika z niego, że ciśnienie zmienia się z wysokością szybciej dla niższych temperatur oraz dla cięższego gazu, i że zmiana ta ma charakter wykładniczy Wzór barometryczny obowiązuje dla atmosfery izotermicznej, dla której mamy oraz jednorodnego pola grawitacyjnego. Jeżeli warunki te nie są spełnione, należy odpowiednio podstawić zależność funkcyjną temperatury od wysokości oraz zależność $g=g(h)$ i rozwiązać otrzymane równanie różniczkowe. Korzystając z faktu, że $\frac{N}{R}=\frac{N_A\cdot m_0}{N_A\cdot k}=\frac{m_0}{k}$ , gdzie $m_0$ - średnia masa cząsteczki powietrza, możemy wzór barometryczny przedstawić w postaci $p=p_0\cdot exp(-\frac{m_0\cdot g\cdot h}{R\cdot T})$