PF Moduł 10: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 26: | Linia 26: | ||
<math>F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | <math>F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
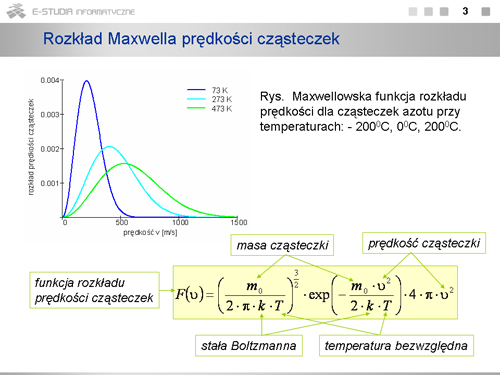
|width="450px" valign="top"|[[Grafika:PF_M10_Slajd3.png]] | |||
|valign="top"|Wyprowadzenie wzoru można znaleźć w literaturze. | |||
<math>F(v)=\left(\frac{m_0}{2\cdot \pi\cdot k\cdot T} \right)^{3/2}\cdot exp\left(-\frac{m_0\cdot v^2}{2\cdot k\cdot T} \right)\cdot 4\cdot \pi \cdot v^2</math> | |||
Co jest charakterystyczne w tym rozkładzie <math>F(v)\,</math> ? Jest to konieczność wystąpienia maksimum ze względu na iloczyn rosnącej parabolicznie i malejącej wykładniczo zależności od <math>v\,</math> . (Przeanalizuj dokładnie trzy człony wzoru na <math>F(v)\,</math> . Pierwszy, to czynnik normalizacyjny zawierający wyłącznie wartości stałe, drugi - to człon wykładniczy, ale z ujemną wartością w wykładniku, czyli malejący ze wzrostem prędkości i równy jedynce dla , ostatni - rosnący paraboliczne ze wzrostem prędkości. Rezultat jest zobrazowany na wykresie maxwellowskiej funkcji rozkładu prędkości cząsteczek azotu przy temperaturach: <math>73 K\, (-200^\circ C)\,</math> , <math>273 K\, (0^\circ C)\,</math> , <math>473 K\, (200^\circ C)\,</math>. Gdy temperatura rośnie maksimum krzywej rozkładu przesuwa się w stronę większych prędkości i krzywa ulega spłaszczeniu. Pole pod krzywą równe jest całkowitej liczbie cząsteczek w próbce i pozostaje stałe niezależnie od temperatury. | |||
Rozkład prędkości cząsteczek w danej temperaturze zależy od masy cząsteczek. Im mniejsza masa tym większa liczba cząsteczek o dużych prędkościach. | |||