PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 184: | Linia 184: | ||
<math>a_n\frac{d^nx_p}{dt^n}+a_{n-1}\frac{d^{n-1}x_p}{dt^{n-1}}+a_{n-2}\frac{d^{n-2}x_p}{dt^{n-2}}+...+a_1\frac{dx_p}{dt}+a_0x_p=0</math> | <math>a_n\frac{d^nx_p}{dt^n}+a_{n-1}\frac{d^{n-1}x_p}{dt^{n-1}}+a_{n-2}\frac{d^{n-2}x_p}{dt^{n-2}}+...+a_1\frac{dx_p}{dt}+a_0x_p=0</math> | ||
Rozwiązanie powyższego równania jednorodnego uzyskuje się za pośrednictwem równania charakterystycznego | Rozwiązanie powyższego równania jednorodnego uzyskuje się za pośrednictwem równania charakterystycznego | ||
<math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s+a+a_0=0</math> | <math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s+a+a_0=0</math> | ||
Jest to wielomian n-tego rzędu zmiennej zespolonej s o współczynnikach rzeczywistych <math>a_i\,</math> Pierwiastki <math> s_i (i=1, 2,..., n)</math> tego wielomianu stanowią '''bieguny układu.''' | Jest to wielomian n-tego rzędu zmiennej zespolonej s o współczynnikach rzeczywistych <math>a_i\,</math> Pierwiastki <math> s_i (i=1, 2,..., n)</math> tego wielomianu stanowią '''bieguny układu.''' | ||
| Linia 201: | Linia 199: | ||
<math>x_p(t)=\Sigma_{i=1}^n A_i e^{s_it}</math> | <math>x_p(t)=\Sigma_{i=1}^n A_i e^{s_it}</math> | ||
W rozwiązaniu tym współczynniki <math>A_i\,</math> są stałymi całkowania, które należy wyznaczyć wykorzystując znajomość warunków początkowych w obwodzie (napięć kondensatorów i prądów cewek w chwili komutacji <math>t=0\,</math>). Z ciągłości prądów cewek i napięć kondensatorów wynika następująca zależność | W rozwiązaniu tym współczynniki <math>A_i\,</math> są stałymi całkowania, które należy wyznaczyć wykorzystując znajomość warunków początkowych w obwodzie (napięć kondensatorów i prądów cewek w chwili komutacji <math>t=0\,</math>). Z ciągłości prądów cewek i napięć kondensatorów wynika następująca zależność | ||
<math>x(0^-)=x(0^+)</math> | <math>x(0^-)=x(0^+)</math> | ||
Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\,</math> i podstawia do wzoru ogólnego . Po wyznaczeniu rozwiązania obwodu dla składowej ustalonej i przejściowej rozwiązanie całkowite jest sumą obu rozwiązań cząstkowych, to znaczy | Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\,</math> i podstawia do wzoru ogólnego . Po wyznaczeniu rozwiązania obwodu dla składowej ustalonej i przejściowej rozwiązanie całkowite jest sumą obu rozwiązań cząstkowych, to znaczy | ||
<math>x(t)=x_u(t)+x_p(t)</math> | <math>x(t)=x_u(t)+x_p(t)</math> | ||
Powyższa procedura rozwiązania stanu nieustalonego w obwodzie poprzez rozwiązanie układu równań różniczkowych wyższego rzędu nosi nazwę '''metody klasycznej'''. Przy większej liczbie zmiennych jest ona dość uciążliwa w obliczeniach, gdyż wymaga pracochłonnego wyznaczania rozwiązań dla każdej składowej przejściowej zmiennych stanu. Dlatego w praktyce stosuje się zwykle tylko do równań pierwszego rzędu. W tej pracy pokażemy jej zastosowanie w rozwiązaniu stanu nieustalonego w obwodzie RL oraz RC przy załączeniu napięcia stałego. | Powyższa procedura rozwiązania stanu nieustalonego w obwodzie poprzez rozwiązanie układu równań różniczkowych wyższego rzędu nosi nazwę '''metody klasycznej'''. Przy większej liczbie zmiennych jest ona dość uciążliwa w obliczeniach, gdyż wymaga pracochłonnego wyznaczania rozwiązań dla każdej składowej przejściowej zmiennych stanu. Dlatego w praktyce stosuje się zwykle tylko do równań pierwszego rzędu. W tej pracy pokażemy jej zastosowanie w rozwiązaniu stanu nieustalonego w obwodzie RL oraz RC przy załączeniu napięcia stałego. | ||
| Linia 231: | Linia 226: | ||
<math>i_{Lu}(t)\frac{E}{R}</math> | <math>i_{Lu}(t) = \frac{E}{R}</math> | ||
|} | |} | ||
| Linia 240: | Linia 235: | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd12.png]] | ||
|valign="top"|Przechodząc do obliczenia stanu przejściowego należy wyeliminować zewnętrzne źródło zasilające. Ponieważ jest to źródło napięciowe, należy go zewrzeć. Schemat obwodu dla stanu przejściowego po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona, ma postać przedstawioną na rysunku. Stosując prawo napięciowe Kirchhoffa dla tego obwodu przy uwzględnieniu | |valign="top"|Przechodząc do obliczenia stanu przejściowego należy wyeliminować zewnętrzne źródło zasilające. Ponieważ jest to źródło napięciowe, należy go zewrzeć. Schemat obwodu dla stanu przejściowego po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona, ma postać przedstawioną na rysunku. Stosując prawo napięciowe Kirchhoffa dla tego obwodu przy uwzględnieniu | ||
<math>u_L_p=\frac{di_{Lp}}{dt}</math> | <math>u_L_p=\frac{di_{Lp}}{dt}</math> | ||
otrzymuje się równanie różniczkowe jednorodne (brak wymuszenia) dla składowej przejściowej o postaci | otrzymuje się równanie różniczkowe jednorodne (brak wymuszenia) dla składowej przejściowej o postaci | ||
<math>L\frac{di_{Lp}}{dt}+Ri_{Lp}=0</math> | <math>L\frac{di_{Lp}}{dt}+Ri_{Lp}=0</math> | ||
Równanie charakterystyczne odpowiadające powyższemu równaniu różniczkowemu przyjmuje postać | Równanie charakterystyczne odpowiadające powyższemu równaniu różniczkowemu przyjmuje postać | ||
<math>Ls+R=0</math> | <math>Ls+R=0</math> | ||
Równanie to posiada tylko jeden pierwiastek | Równanie to posiada tylko jeden pierwiastek | ||
<math>s_1=-\frac{R}{L}</math> | <math>s_1=-\frac{R}{L}</math> | ||
Wykorzystując wzór na rozwiązanie stanu przejściowego dla prądu w obwodzie RL zapiszemy w postaci | |||
Wykorzystując wzór rozwiązanie stanu przejściowego dla prądu w obwodzie RL zapiszemy w postaci | |||
<math>i_{Lp}=A_1e^{-\frac{t}{L/R}}</math> | <math>i_{Lp}=A_1e^{-\frac{t}{L/R}}</math> | ||
w której współczynnik <math>A_1</math> jest nieznaną stałą całkowania. Rozwiązanie całkowite obwodu jest sumą składowej ustalonej i przejściowej. W związku z powyższym prąd cewki określony jest następującym wzorem | w której współczynnik <math>A_1</math> jest nieznaną stałą całkowania. Rozwiązanie całkowite obwodu jest sumą składowej ustalonej i przejściowej. W związku z powyższym prąd cewki określony jest następującym wzorem | ||
<math>i_L(t)=i_{Lu}(t)+i_{Lp}(t)=\frac{E}{R}+A_1e^{-\frac{t}{L/R}}</math> | <math>i_L(t)=i_{Lu}(t)+i_{Lp}(t)=\frac{E}{R}+A_1e^{-\frac{t}{L/R}}</math> | ||
| Linia 279: | Linia 263: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd13.png]] | ||
|valign="top"|Z prawa komutacji dla cewki wynika, że <math>i_L(0^-)=i_L(0+)</math> , stąd wobec <math>i_L(0^-)=0</math> otrzymuje się | |valign="top"|Z prawa komutacji dla cewki wynika, że <math>i_L(0^-)=i_L(0^+)</math>, stąd wobec <math>i_L(0^-)=0</math> otrzymuje się | ||
<math>0=\frac{E}{R}+A_1</math> | |||
oraz | oraz | ||
<math>A_1=-E/R</math> | <math>A_1=-E/R</math> | ||
Stąd rozwiązanie określające przebieg prądu cewki w stanie nieustalonym przyjmuje postać | Stąd rozwiązanie określające przebieg prądu cewki w stanie nieustalonym przyjmuje postać | ||
<math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{L/R}})</math> | <math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{L/R}})</math> | ||
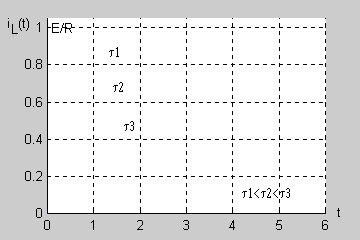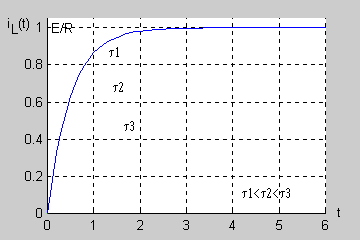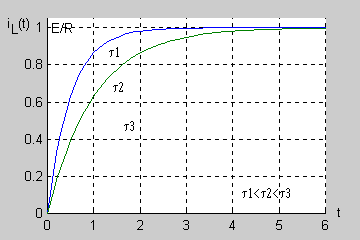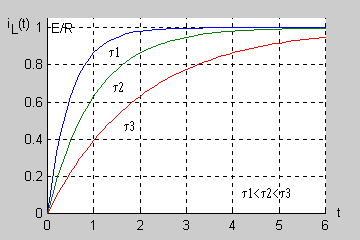
Wprowadzając pojęcie stałej czasowej <math>\tau\,</math> obwodu RL | Wprowadzając pojęcie stałej czasowej <math>\tau\,</math> obwodu RL | ||
<math>\tau=\frac{L}{R}</math> | <math>\tau=\frac{L}{R}</math> | ||
rozwiązanie na prąd cewki w stanie nieustalonym można zapisać w postaci | rozwiązanie na prąd cewki w stanie nieustalonym można zapisać w postaci | ||
<math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{\tau}})</math> | <math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{\tau}})</math> | ||
Jednostką stałej czasowej jest sekunda (jednostką indukcyjności jest <math>1H = 1\Omega s</math> a jednostką rezystancji <math>1\Omega</math>). Łatwo wykazać, że po upływie trzech stałych czasowych <math>(t=3\tau )</math> prąd cewki uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po 5 stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony. | Jednostką stałej czasowej jest sekunda (jednostką indukcyjności jest <math>1H = 1\Omega s</math> a jednostką rezystancji <math>1\Omega</math>). Łatwo wykazać, że po upływie trzech stałych czasowych <math>(t=3\tau )</math> prąd cewki uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po 5 stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony. | ||
| Linia 317: | Linia 290: | ||
Jest to przebieg typu wykładniczego, w którym stan przejściowy trwa tym dłużej im dłuższa jest stała czasowa. Praktycznie po 5 stałych czasowych stan przejściowy w obwodzie zanika przechodząc w stan ustalony. | Jest to przebieg typu wykładniczego, w którym stan przejściowy trwa tym dłużej im dłuższa jest stała czasowa. Praktycznie po 5 stałych czasowych stan przejściowy w obwodzie zanika przechodząc w stan ustalony. | ||
|} | |} | ||
Wersja z 13:36, 24 sie 2006

|
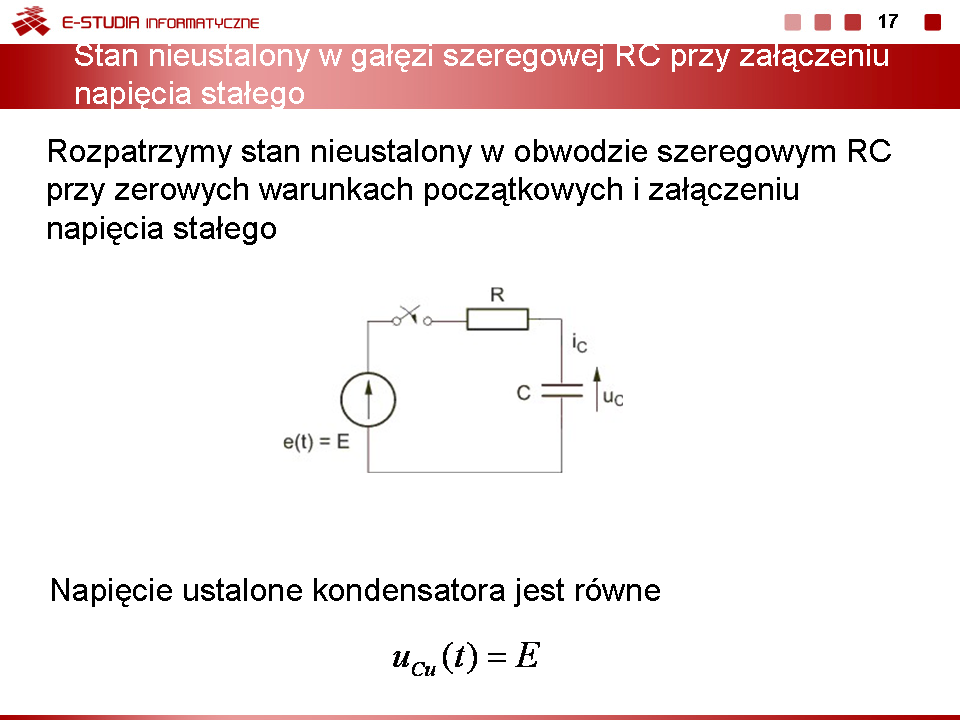
Metoda równań różniczkowych w rozwiązaniu stanu nieustalonego w obwodach elektrycznych |
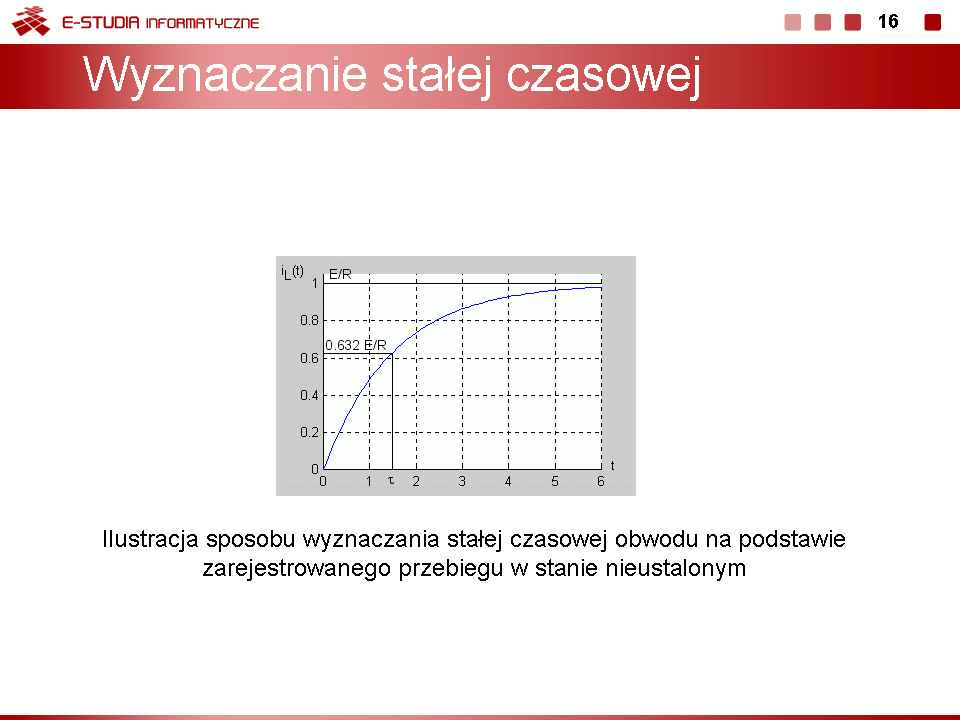
| Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość
|
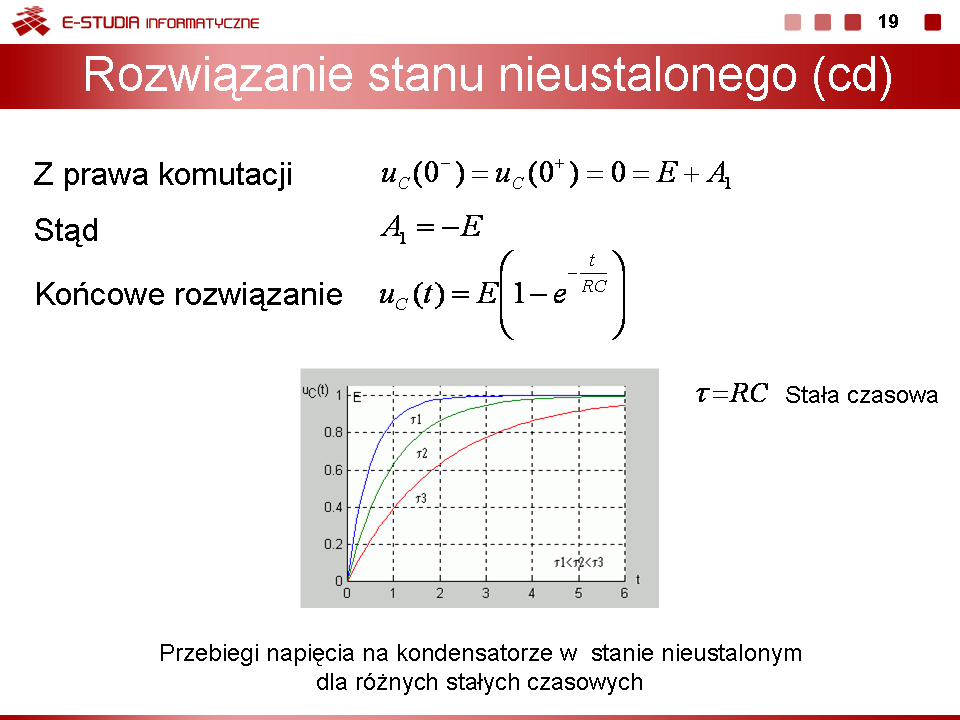
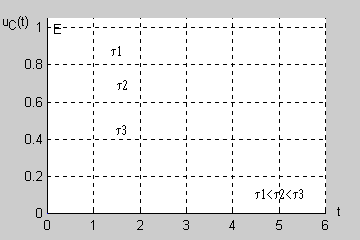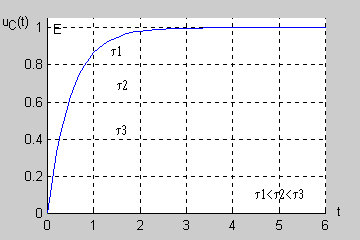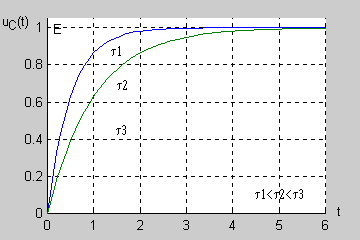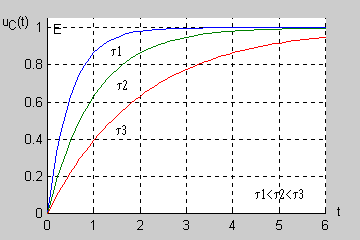
| Łatwo wykazać, że po upływie 3 stałych czasowych ( ) napięcie uzyskuje prawie 95% swojej wartości ustalonej a po 5 stałych czasowych aż 99,3%. Oznacza to, że praktycznie po stałych czasowych stan nieustalony w obwodzie zanika przechodząc w stan ustalony.
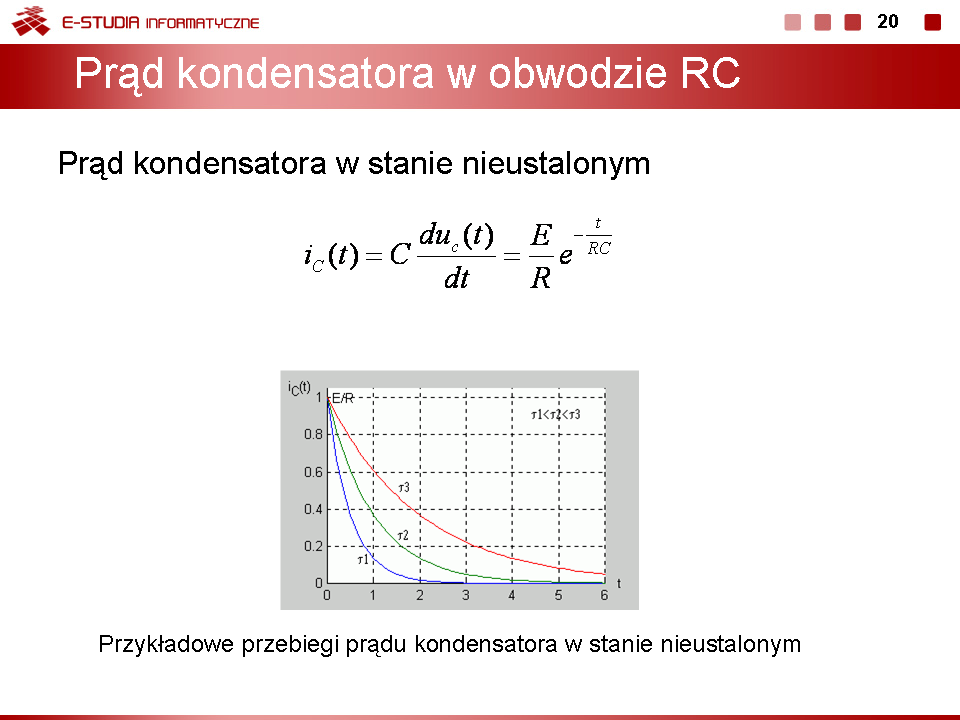
Stałą czasową można wyznaczyć bezpośrednio na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i pojemności, podobnie jak to miało miejsce w przypadku obwodu RL. |
| Zadania sprawdzające
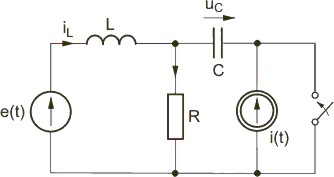
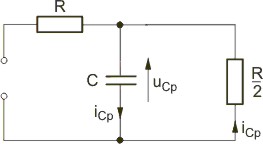
Zadanie 7.1 Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: Rozwiązanie Warunki początkowe dotyczą stanu ustalonego przed przełączeniem, w którym w obwodzie działają oba źródła wymuszające. Stosując metodę symboliczną analizy obwodu otrzymujemy
|

|
Równania obwodu w stanie ustalonym
Warunki początkowe:
|
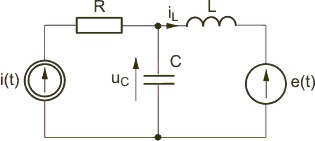
| Zadanie 7.2
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku Rozwiązanie Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
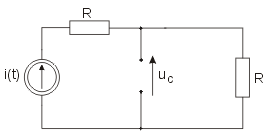
Rozwiązanie Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
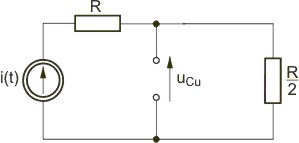
Schemat obwodu w stanie ustalonym po przełączeniu
Schemat obwodu w stanie przejściowym po przełączeniu
Postać ostateczna rozwiązania:
|