PF Moduł 9

Wprowadzenie Wszelkie substancje z punktu widzenia mikroskopowego mają budowę "ziarnistą". Składnikami ich są atomy bądź cząsteczki, których wzajemne oddziaływania określają własności makroskopowe substancji jak ciśnienie lub temperatura oraz stan skupienia: stały, ciekły lub gazowy. Ogromna liczba cząsteczek, z jaką zwykle mamy do czynienia uniemożliwia stosowanie do opisu ich ruchu równań Newtona w takim sensie, jak się to czyni w mechanice. W jednym centymetrze sześciennym gazu mieści się w warunkach normalnych około $10^{19}$ cząsteczek, które zderzają się ze sobą oraz ze ściankami naczynia. Do opisu ich ruchu stosuje się metody statystyczne, a wielkości makroskopowe charakteryzuje się poprzez uśrednione wartości wielkości mikroskopowych takich jak prędkości cząsteczek czy energie ich wzajemnego oddziaływania.

---

Czym jest ciśnienie gazu z mikroskopowego punktu widzenia? Ścianki naczynia zawierającego pewną porcję gazu uderzane są ustawicznie przez cząsteczki będące w chaotycznym ruchu. Wyznaczmy przekaz pędu przy takich zderzeniach. Dla uproszczenia przyjmijmy, że naczynie ma kształt sześcianu o długości ścianek równej $l$ .

---

W układzie współrzędnych prostokątnych rozważamy sprężyste zderzenie cząsteczki gazu, o wektorze prędkości $v$, ze ścianką naczynia prostopadłą do osi $X$. Prędkość cząsteczki zapiszemy w postaci wektora $\overrightarrow{v}=(v_x,v_y,v_z)$ Po odbiciu się od ścianki naczynia cząsteczka porusza się z prędkością $v^{\prime }$. W wyniku sprężystego zderzenia cząsteczki ze ścianką prostopadłą do osi $X$ zmieni znak tylko składowa prędkości wzdłuż tej osi, czyli będzie ${v^{\prime }}_x=-v_x$ , ${v^{\prime }}_y=-v_y$ , ${v^{\prime }}_z=-v_z$ Dalsze nasze rozważania dotyczyć będą tylko kierunku $X$ , stosować będziemy zapis skalarny.

---

Zmiana składowej pędu wzdłuż osi $X$ będzie różnicą pomiędzy pędem po i przed zderzeniem (Pęd oznaczamy tu dużą literą $P$ , bowiem małą litera oznaczać będziemy ciśnienie.) $\mathrm{\Delta }{P}_x=-m\cdot v_x-(m\cdot v_x)=-2m\cdot v_x$ Pęd przekazany ściance będzie odwrotnego znaku, a więc wyniesie $2m\cdot v_x$ .

---

Czas przelotu cząsteczki przez kostkę wynosi $t=l/v_x$ , zaś przelot w obie strony trwać będzie dwa razy dłużej; $\mathrm{\Delta }t=2\cdot l/v_x$ . Częstość $\nu$ uderzeń o ściankę, czyli liczba uderzeń w jednostce czasu będzie odwrotnością czasu przelotu cząsteczki w dwie strony, czyli $\nu =1/\mathrm{\Delta }t=v_x/(2\cdot l)$ . Pęd przekazany ściance w jednostce czasu równy będzie pędowi przekazanemu w jednym uderzeniu pomnożonemu przez liczbę uderzeń w jednostce czasu. $\frac{\mathrm{\Delta }{P}_x}{\mathrm{\Delta }t}=\frac{v_x}{2\cdot l}\cdot 2\cdot m\cdot v_x=\frac{m\cdot {v^2}_x}{l}$

---

Z drugiej zasady dynamiki wiemy, że $\mathrm{\Delta }P/\mathrm{\Delta }t=F$ . Pamiętamy też, że ciśnienie jest stosunkiem siły do powierzchni, na którą siła działa. Powierzchnia ta jest w naszym przypadku równa kwadratowi boku ścianki. Ciśnienie będące skutkiem uderzeń jednej cząsteczki w ściankę wynosi, więc $p=F/S=F/l^2$ . Sumując przyczynki od wszystkich uderzających w ściankę cząsteczek otrzymujemy wyrażenie na ciśnienie gazu działające na ściankę Założyliśmy tu, że wszystkie cząsteczki w liczbie $N$ mają tę samą masę $m$ . Długość ścianki w trzeciej potędze zamieniliśmy objętością sześcianu $V$ . Iloczyn masy cząsteczki m przez liczbę cząsteczek $N$ jest masą gazu w naczyniu, zaś podzielony przez objętość $V$ jest gęstością gazu, którą oznaczyliśmy symbolem $\rho$ . Symbol $⟨{v^2}_x⟩$ oznacza wartość średnią kwadratu składowej wektora prędkości wzdłuż osi $X$ .

---

Biorąc pod uwagę, że kwadrat wektora równy jest sumie kwadratów jego składowych ${\overrightarrow{v}}^2=v^2={v^2}_x+{v^2}_y+{v^2}_z$ i pamiętając, że wszystkie kierunki wektora prędkości są tak samo prawdopodobne oraz, że ruchy w każdym kierunku są niezależne - możemy zamienić wartość średnią kwadratu składowej przez wartość średnią kwadratu wektora prędkości, czyli $⟨{v^2}_x⟩=\frac{1}{3}⟨v^2⟩$ Ostatecznie otrzymujemy wzór wyrażający związek pomiędzy mikroskopowymi (średnia prędkość cząsteczek) i makroskopowymi (ciśnienie i gęstość) własnościami gazu $p=\frac{1}{3}\cdot \frac{m\cdot N}{V}\cdot ⟨v^2⟩=\frac{1}{3}\cdot \rho \cdot ⟨v^2⟩$ W naszych rozważaniach nie uwzględnialiśmy zderzeń pomiędzy cząsteczkami. Zwróćmy jednak uwagę, że w zderzeniach sprężystych jest zachowany pęd oraz energia kinetyczna, a więc przy dużej liczbie zderzających się cząsteczek zderzenia te nie będą wpływać na wartość średnią pędu przekazywanego ściankom naczynia. Wybraliśmy także regularny (sześcienny) kształt naczynia. W warunkach równowagi ciśnienie wywierane na wszystkie ścianki o dowolnym kształcie a także wewnątrz naczynia jest jednakowe, o czym wiemy z prawa Pascala. Rozważania nasze mają, więc ogólny charakter.

---

Dla znalezienia związku pomiędzy makroskopową i mikroskopową interpretacją temperatury pomnóżmy lewą i prawą stronę równania opisującego ciśnienie gazu przez objętość naczynia $V$ i porównajmy to wyrażenie z równaniem stanu gazu doskonałego $p\cdot V=\frac{1}{3}\cdot \rho ⟨v^2⟩\cdot V=\frac{1}{3}\cdot \begin{array}{c}{n}_M\cdot M\\ \overbrace{\rho \cdot V}\end{array}\cdot ⟨v^2⟩$ We wzorze tym iloczyn gęstości i objętości jest po prostu masą gazu, którą następnie wyraziliśmy w molach oznaczając przez $M$ jego masę molową.

---

Teraz masę gazu wyraziliśmy w molach, oznaczając przez $M$ jego masę molową. Mnożąc stronami przez $3/2$ i dzieląc przez liczbę Avogadro otrzymujemy $\frac{1}{2}\cdot \begin{array}{c}{m}_0\\ \overbrace{\frac{M}{N_A}}\end{array}\cdot ⟨v^2⟩=\frac{3}{2}\cdot \begin{array}{c}k\\ \overbrace{\frac{R}{N_A}}\end{array}\cdot T$ Zauważamy przy tym, że masa molowa podzielona przez liczbę Avogadro to po prostu masa jednej cząsteczki $m_0$ . Iloraz stałej gazowej i liczby Avogadro, to stała Boltzmanna $k$ . Stała ta ma sens stałej gazowej odniesionej do jednej cząsteczki. Jak zobaczymy, stała ta odgrywa fundamentalna rolę w fizyce. Wykorzystując wprowadzone oznaczenia możemy przepisać ostatnie równanie w postaci $\frac{1}{2}\cdot m_0\cdot ⟨v^2⟩=⟨\frac{1}{2}\cdot m_0\cdot v^2⟩=\frac{3}{2}\cdot k\cdot T$ Wyrażenie po lewej stronie jest wielkością mikroskopową - średnią energią kinetyczną chaotycznego ruchu cząsteczek gazu przypadającą na jedną cząsteczkę; wyrażenie po prawej stronie jest proporcjonalne do wielkości makroskopowej - temperatury bezwzględnej ciała. Stwierdzamy, więc temperatura jest miarą średniej energii kinetycznej chaotycznego ruchu cząsteczek.

---

Średnia wartość kwadratu prędkości wynosi $⟨v^2⟩=\frac{3\cdot k\cdot T}{m_0}$ Na tej podstawie możemy określić tzw. średnią prędkość kwadratową definiując ją jako Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_{śr. kw.}=\sqrt{\left\langle v^2\right\rangle}=\sqrt{\frac{3\cdot k\cdot T}{m_0}}} Zauważmy, że możemy średnią prędkość kwadratową wyrazić poprzez wielkości makroskopowe: ciśnienie $p$ i gęstość gazu $\rho$ , bowiem również Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_{śr. kw.}=\sqrt{\frac{3\cdot p}{\rho}}} . Mamy, więc ideę prostego eksperymentu, za pomocą, którego określając łatwo mierzalne wielkości makroskopowe: $p$ (manometr) oraz objętość i masę gazu w celu wyznaczenia jego gęstości $\rho$ , możemy wyznaczyć statystycznie uśrednioną wielkość mikroskopową, jaką jest Parser nie mógł rozpoznać (błąd składni): {\displaystyle v_{śr. kw.}\,} .

---

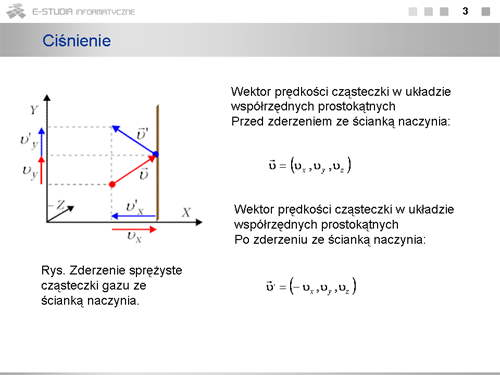
W naszych rozważaniach uwzględnialiśmy tylko energię ruchu postępowego cząsteczek. Jest to wystarczające, jeżeli rozpatrujemy gaz jednoatomowy - kiedy atomy możemy traktować jako punkty materialne. Do opisu ich położenia wystarczy podanie trzech współrzędnych. Cząsteczki wieloatomowe mogą wykonywać także ruch obrotowy; możliwe są również drgania atomów wchodzących w skład cząsteczki. Z ruchami tymi także wiąże się pewna energia (z obrotem - energia kinetyczna ruchu obrotowego, z drganiami - energia kinetyczna i energia potencjalna). Położenie punktu materialnego w przestrzeni jest w pełni opisane przez trzy współrzędne. Dwa połączone na sztywno punkty materialne mogą być opisane za pomocą pięciu (a nie sześciu) liczb, bowiem fakt ich sztywnego połączenia sprawia, że do opisu ich położenia wystarczy podać położenie jednego z nich oraz dwa kąty określające orientację w przestrzeni prostej łączącej te punkty. Położenie drugiego punktu na tej prostej jest znane, skoro znana jest ich wzajemna odległość. Położenie N niezależnych punktów materialnych wymaga jednak 3N liczb, skoro traktujemy te punkty jako niezależne. Położenie ciała sztywnego wymaga podania sześciu liczb. Pięć z nich określa, podobnie jak w przypadku układu dwóch ciał, położenie wybranego punktu, na przykład środka ciężkości, oraz kierunek wybranej prostej, na przykład osi obrotu. Punkty nie znajdujące się na osi mogą jednak zmieniać swe położenie wskutek ruch obrotowego wokół osi, potrzeba wiec jeszcze znać kąt obrotu - razem sześć liczb. Liczbę niezależnych wielkości za pomocą, których może być opisane położenie układu nazywamy liczbą stopni swobody układu. Liczba ta określa, możliwości ruchów, jakie może wykonywać cząsteczka. Z każdym ruchem wiąże się określona energia. Jeżeli ruch jest całkowicie chaotyczny i żaden rodzaj ruchu nie jest uprzywilejowany, to można przyjąć, że na każdy stopień swobody przypada jednakowa porcja energii. Stwierdzenie to jest treścią zasady ekwipartycji energii, czyli inaczej mówiąc, zasady równomiernego rozdziału energii na wszystkie stopnie swobody. Zasada ekwipartycji energii Na każdy stopień swobody cząsteczki przypada średnio ta sama energia. Jej wartość możemy określić na przykładzie ruchu postępowego cząsteczek punktowych. W tym przypadku liczba stopni swobody wynosi 3, a średnia energia kinetyczna cząsteczki, jest równa $3/2\cdot k\cdot T$ . Możemy uzupełnić ilościowo treść zasady ekwipartycji energii. Na każdy stopień swobody cząsteczki przypada średnio energia równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle kT/2\} . W oparciu o nasze rozważania widzimy, że energia ruchu cząsteczek w gazach wieloatomowych jest większa niż w gazach jednoatomowych.

---

Średnia energia cząsteczki o danej liczbie stopni swobody $i$ wynosi $⟨E⟩=\frac{i}{2}\cdot k\cdot T$ Dla $N$ cząsteczek gazu doskonałego, kiedy zaniedbuje się energię potencjalną wynikającą z sił wzajemnego oddziaływania cząsteczek, iloczyn $N⟨E⟩$ jest po prostu energią wewnętrzną gazu równą $U=N\cdot ⟨E⟩=N\cdot \frac{i}{2}\cdot k\cdot T$ Dla $n_M$ moli gazu doskonałego $U=n_M\cdot N_A\cdot \frac{i}{2}\cdot k\cdot T=n_M\cdot \frac{i}{2}\cdot k\cdot T$ Energię wewnętrzną układu $U$ utożsamiamy z całkowitą energia wszystkich cząsteczek. Ponieważ dla $n_M$ moli gazu doskonałego $dU=n_M\cdot C_V\cdot dT$ więc, otrzymujemy $C_V=\frac{1}{n_M}\cdot \frac{dU}{dT}=\frac{i}{2}\cdot R$ Wykorzystując wzór Mayera, $C_p-C_V=R$ $C_p=\frac{i+2}{2}\cdot R$ Za pomocą liczby stopni swobody cząsteczki gazu można też wyrazić wykładnik adiabaty $\kappa =\frac{C_p}{C_V}$ $\kappa =\frac{i+2}{i}$