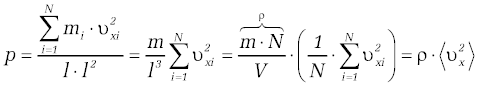PF Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 161: | Linia 161: | ||
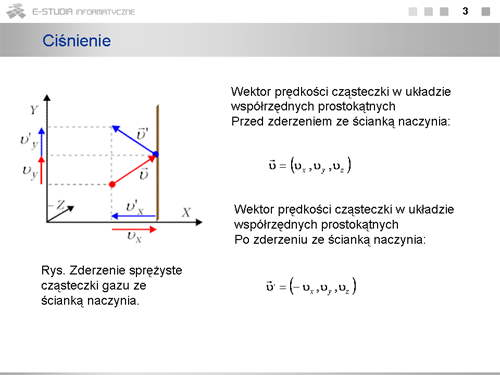
Dla <math>N\,</math> cząsteczek gazu doskonałego, kiedy zaniedbuje się energię potencjalną wynikającą z sił wzajemnego oddziaływania cząsteczek, iloczyn <math>N\left\langle E\right\rangle\,</math> jest po prostu energią wewnętrzną gazu równą | Dla <math>N\,</math> cząsteczek gazu doskonałego, kiedy zaniedbuje się energię potencjalną wynikającą z sił wzajemnego oddziaływania cząsteczek, iloczyn <math>N\left\langle E\right\rangle\,</math> jest po prostu energią wewnętrzną gazu równą | ||
:<math>U=N\left\langle E\right\rangle=N\cdot\frac{i}{2}\cdot k\cdot T</math> | :<math>U=N\cdot \left\langle E\right\rangle=N\cdot\frac{i}{2}\cdot k\cdot T</math> | ||
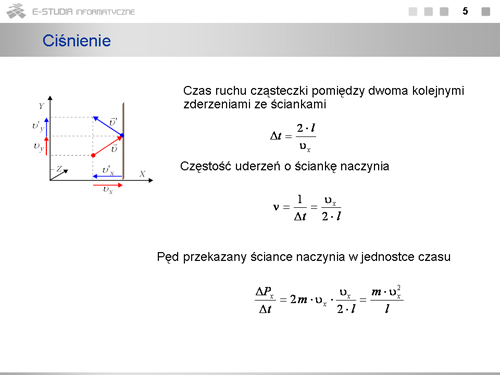
Dla <math>n_M\,</math> moli gazu doskonałego | Dla <math>n_M\,</math> moli gazu doskonałego | ||
:<math>U=n_M\cdot N_A\cdot\frac{i}{2}\cdot k\cdot T=n_M | :<math>U=n_M\cdot N_A\cdot\frac{i}{2}\cdot k\cdot T=n_M\cdot\frac{i}{2}\cdot k\cdot T</math> | ||
Energię wewnętrzną układu <math>U\,</math> utożsamiamy z całkowitą energia wszystkich cząsteczek. | |||
Ponieważ dla <math>n_M\,</math> moli gazu doskonałego | |||
:<math>dU=n_M\cdot c_V\cdot dT</math> | |||
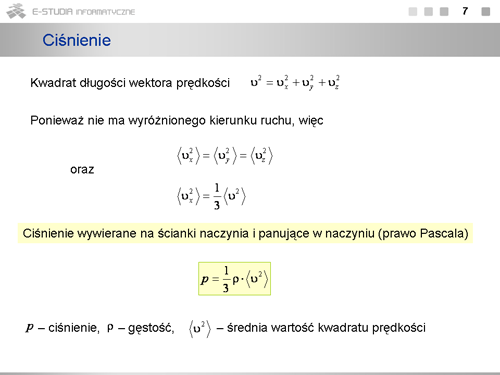
więc, otrzymujemy | |||
:<math>C_V=\frac{1}{n_M}\cdot \frac{dU}{dT}=\frac{i}{2}\cdot R </math> | |||