PEE Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 325: | Linia 325: | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd22.png]] | ||
|valign="top"|Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji <math>X_{L1}=Kz_1^2, X_{L2}=Kz_2^2, X_M=Kz_1z_2</math> gdzie K oznacza pewną stałą konstrukcyjną, to z zależności wynika | |valign="top"|Jeśli uwzględnimy, że reaktancje cewek są proporcjonalne do liczby zwojów według relacji <math>X_{L1}=Kz_1^2, X_{L2}=Kz_2^2, X_M=Kz_1z_2</math> gdzie K oznacza pewną stałą konstrukcyjną, to z zależności wynika | ||
<math>\frac{U_2}{U_1}=-\frac{z_2}{z_1}=-\frac{1}{n}</math> | <math>\frac{U_2}{U_1}=-\frac{z_2}{z_1}=-\frac{1}{n}</math> | ||
| Linia 337: | Linia 336: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd23.png]] | ||
|valign="top"| | |valign="top"|Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej <math>n=2\,</math>. Przyjmiemy następujące wartości parametrów obwodu: <math>e(t)=10\sqrt2sin(\omega t)V, \omega=1rad/s, R=5\Omega, C=0,2F</math>. | ||
|} | |} | ||
| Linia 348: | Linia 345: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M5_Slajd24.png]] | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd24.png]] | ||
|valign="top"| | |valign="top"|Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami | ||
Wielkości symboliczne charakteryzujące elementy obwodu | |||
<math>E=10</math> | <math>E=10</math> | ||
<math>Z_C=-\frac{j}{\omega C}=-j5</math> | <math>Z_C=-\frac{j}{\omega C}=-j5</math> | ||
| Linia 360: | Linia 354: | ||
Układ równań opisujących obwód | Układ równań opisujących obwód wynika z praw Kirchhoffa i równań transformatora idealnego | ||
<math>E=RI_1+U_1</math> | <math>E=RI_1+U_1</math> | ||
| Linia 376: | Linia 369: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M5_Slajd25.png]] | ||
|valign="top"|Po wstawieniu wartości liczbowych otrzymuje się | |valign="top"|Po wstawieniu wartości liczbowych otrzymuje się | ||
Wersja z 13:01, 24 sie 2006

|
Wykład 5. Obwody ze sprzężeniami magnetycznymi |
|
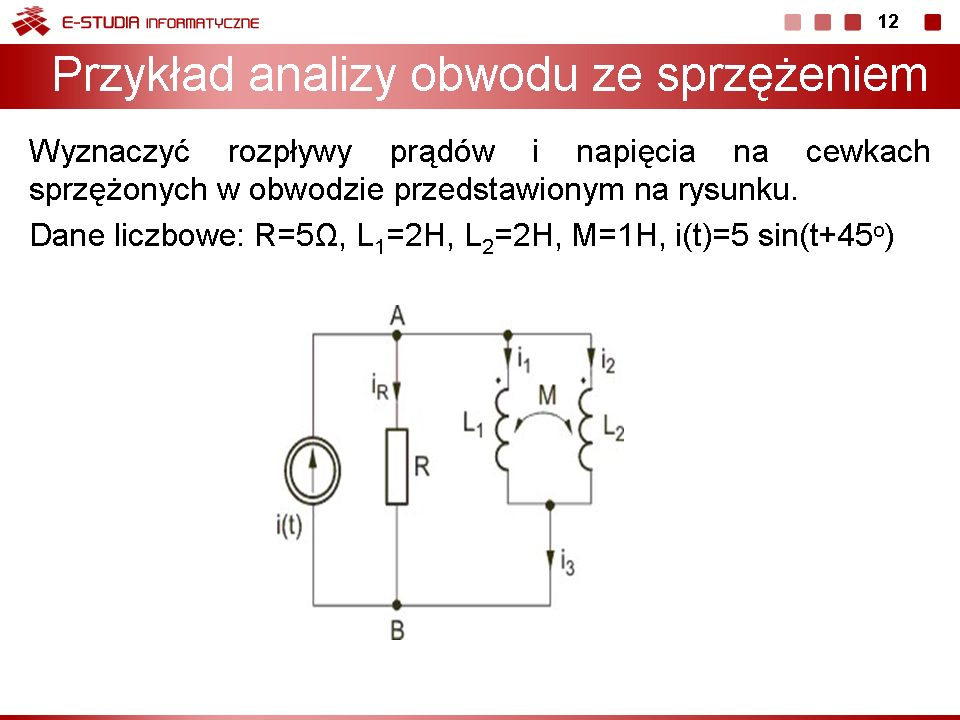
Jako przykład wyznaczymy rozpływy prądów w obwodzie (slajd obok) ze sprzężeniem magnetycznym.
Przyjąć następujące wartości parametrów elementów obwodu: oraz . |

|
Pierwszym etapem rozwiązania jest eliminacja sprzężenia magnetycznego. Rysunek na slajdzie przedstawia postać obwodu po eliminacji sprzężenia magnetycznego. |

|
Rozwiązanie obwodu przebiega w następującej kolejności.
Najpierw wyznaczamy wielkości symboliczne charakteryzujące elementy obwodu:
|

|
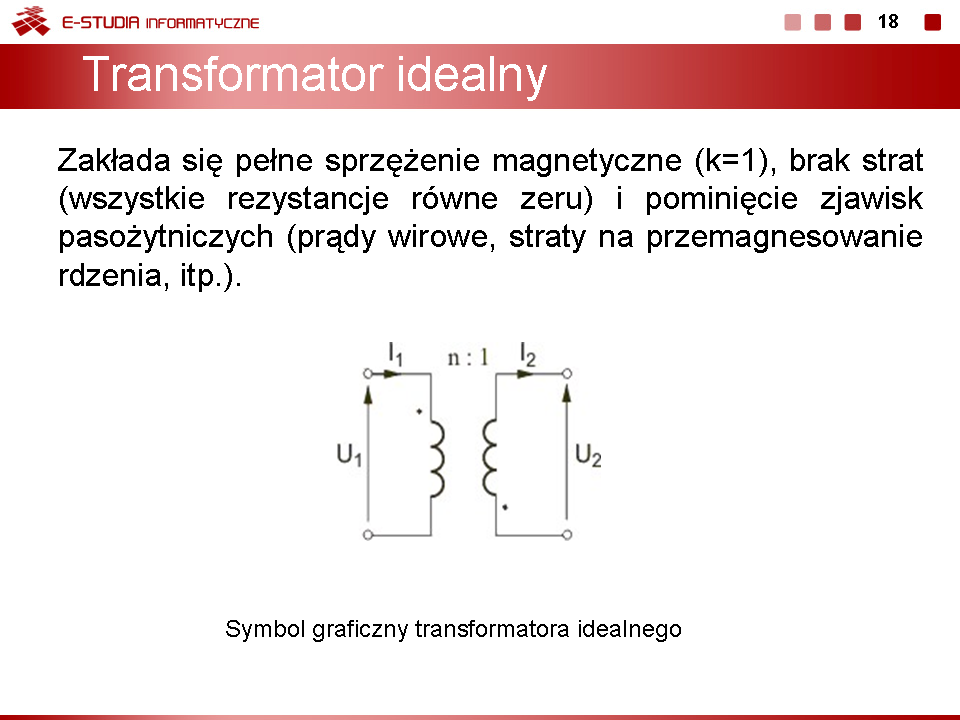
Jako przykład wyznaczymy rozwiązanie obwodu z rysunku zawierającego transformator idealny o przekładni zwojowej równej . Przyjmiemy następujące wartości parametrów obwodu: . |

|
Wielkości symboliczne charakteryzujące elementy obwodu określone są zależnościami
|

|
Po wstawieniu wartości liczbowych otrzymuje się
Po uproszczeniu tego układu równań otrzymuje się
Stąd
Łatwo sprawdzić, że stosunek prądu do prądu podczas gdy
|