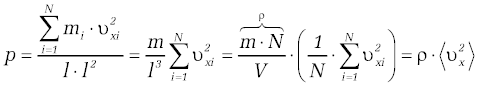PF Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 64: | Linia 64: | ||
Założyliśmy tu, że wszystkie cząsteczki w liczbie <math>N\,</math> mają tę samą masę <math>m\,</math> . Długość ścianki w trzeciej potędze zamieniliśmy objętością sześcianu <math>V\,</math> . Iloczyn masy cząsteczki m przez liczbę cząsteczek <math>N\,</math> jest masą gazu w naczyniu, zaś podzielony przez objętość <math>V\,</math> jest gęstością gazu, którą oznaczyliśmy symbolem <math>\rho\,</math> . Symbol <math>\left \langle {v^2}_x\right \rangle\,</math> oznacza wartość średnią kwadratu składowej wektora prędkości wzdłuż osi <math>X\,</math> . | Założyliśmy tu, że wszystkie cząsteczki w liczbie <math>N\,</math> mają tę samą masę <math>m\,</math> . Długość ścianki w trzeciej potędze zamieniliśmy objętością sześcianu <math>V\,</math> . Iloczyn masy cząsteczki m przez liczbę cząsteczek <math>N\,</math> jest masą gazu w naczyniu, zaś podzielony przez objętość <math>V\,</math> jest gęstością gazu, którą oznaczyliśmy symbolem <math>\rho\,</math> . Symbol <math>\left \langle {v^2}_x\right \rangle\,</math> oznacza wartość średnią kwadratu składowej wektora prędkości wzdłuż osi <math>X\,</math> . | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd7.png]] | |||
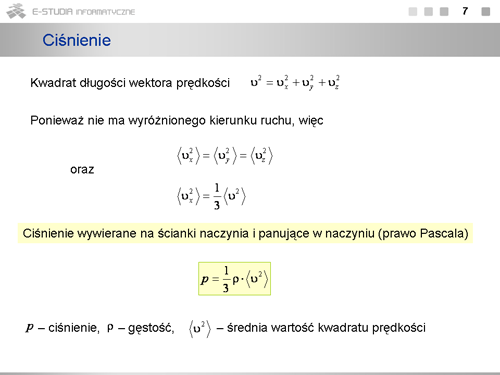
|valign="top"|Biorąc pod uwagę, że kwadrat wektora równy jest sumie kwadratów jego składowych <math>{\vec{v}}^2=v^2={v^2}_x+{v^2}_y+{v^2}_z</math> i pamiętając, że wszystkie kierunki wektora prędkości są tak samo prawdopodobne oraz, że ruchy w każdym kierunku są niezależne - możemy zamienić wartość średnią kwadratu składowej przez wartość średnią kwadratu wektora prędkości, czyli | |||
:<math>\left \langle {v^2}_x\right \rangle =\frac{1}{3}\left \langle v^2\right \rangle</math> | |||
Ostatecznie otrzymujemy wzór wyrażający '''związek pomiędzy mikroskopowymi''' (średnia prędkość cząsteczek) '''i makroskopowymi''' (ciśnienie i gęstość) '''własnościami gazu''' | |||
<math>p=\frac{1}{3}\cdot \frac{m\cdot N}{V}\cdot \left \langle v^2\right \rangle =\frac{1}{3}\cdot \rho\cdot \left \langle v^2\right \rangle</math> | |||
W naszych rozważaniach nie uwzględnialiśmy zderzeń pomiędzy cząsteczkami. Zwróćmy jednak uwagę, że w zderzeniach sprężystych jest zachowany pęd oraz energia kinetyczna, a więc przy dużej liczbie zderzających się cząsteczek zderzenia te nie będą wpływać na wartość średnią pędu przekazywanego ściankom naczynia. Wybraliśmy także regularny (sześcienny) kształt naczynia. W warunkach równowagi ciśnienie wywierane na wszystkie ścianki o dowolnym kształcie a także wewnątrz naczynia jest jednakowe, o czym wiemy z prawa Pascala. Rozważania nasze mają, więc ogólny charakter. | |||