PF Moduł 9: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 39: | Linia 39: | ||
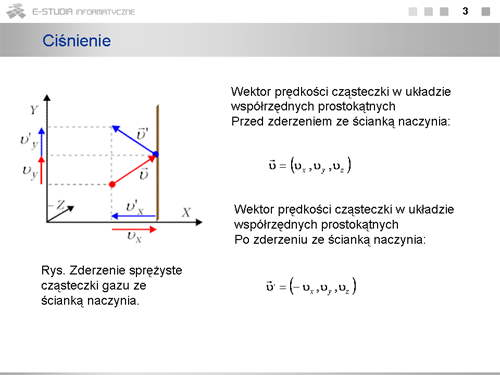
|valign="top"|Zmiana składowej pędu wzdłuż osi <math>X\,</math> będzie różnicą pomiędzy pędem po i przed zderzeniem (Pęd oznaczamy tu dużą literą <math>P\,</math> , bowiem małą litera oznaczać będziemy ciśnienie.) | |valign="top"|Zmiana składowej pędu wzdłuż osi <math>X\,</math> będzie różnicą pomiędzy pędem po i przed zderzeniem (Pęd oznaczamy tu dużą literą <math>P\,</math> , bowiem małą litera oznaczać będziemy ciśnienie.) | ||
<math>\Delta | <math>\Delta P_x=-m\cdot v_x-(m\cdot v_x)=-2m\cdot v_x</math> | ||
Pęd przekazany ściance będzie odwrotnego znaku, a więc wyniesie <math>2m\cdot v_x\,</math> . | Pęd przekazany ściance będzie odwrotnego znaku, a więc wyniesie <math>2m\cdot v_x\,</math> . | ||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd5.png]] | |||
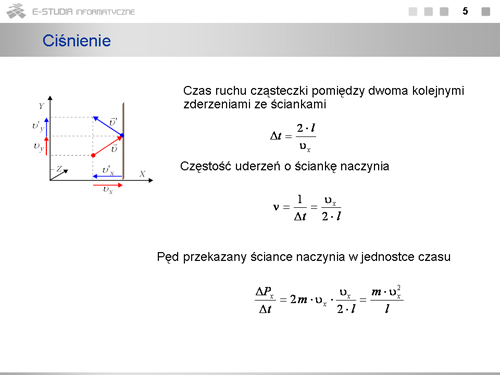
|valign="top"|Czas przelotu cząsteczki przez kostkę wynosi <math>t=l/v_x\,</math> , zaś przelot w obie strony trwać będzie dwa razy dłużej; <math>\Delta t=2\cdot l/v_x\,</math> . Częstość <math>\nu\,</math> uderzeń o ściankę, czyli liczba uderzeń w jednostce czasu będzie odwrotnością czasu przelotu cząsteczki w dwie strony, czyli <math>\nu=1/{\Delta t}=v_x/(2\ cdot l)</math> . Pęd przekazany ściance w jednostce czasu równy będzie pędowi przekazanemu w jednym uderzeniu pomnożonemu przez liczbę uderzeń w jednostce czasu. | |||
: | |||