PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 46: | Linia 46: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd5.png]] | ||
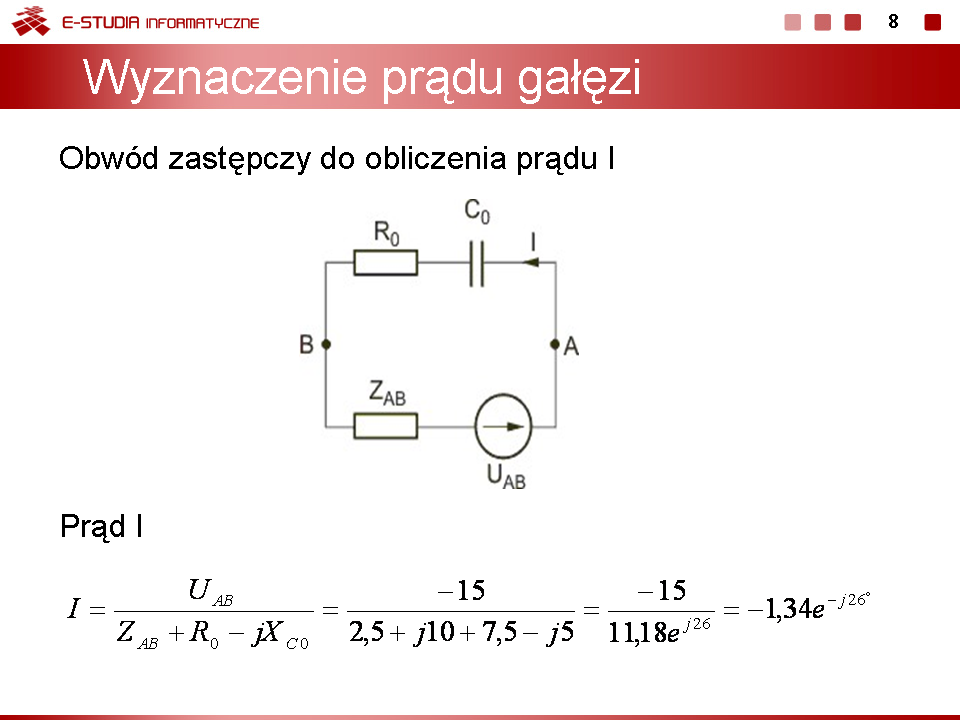
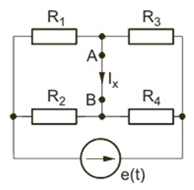
|valign="top"| | |valign="top"|Jako przykład rozpatrzymy obliczenie prądu w gałęzi AB obwodu przedstawionego na slajdzie. | ||
Twierdzenie Thevenina jest tu wyjątkowo użyteczne, gdyż pozwala wyznaczyć wybrany prąd obwodu bez konieczności analizy całego obwodu. | |||
|} | |} | ||
| Linia 53: | Linia 55: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png]] | ||
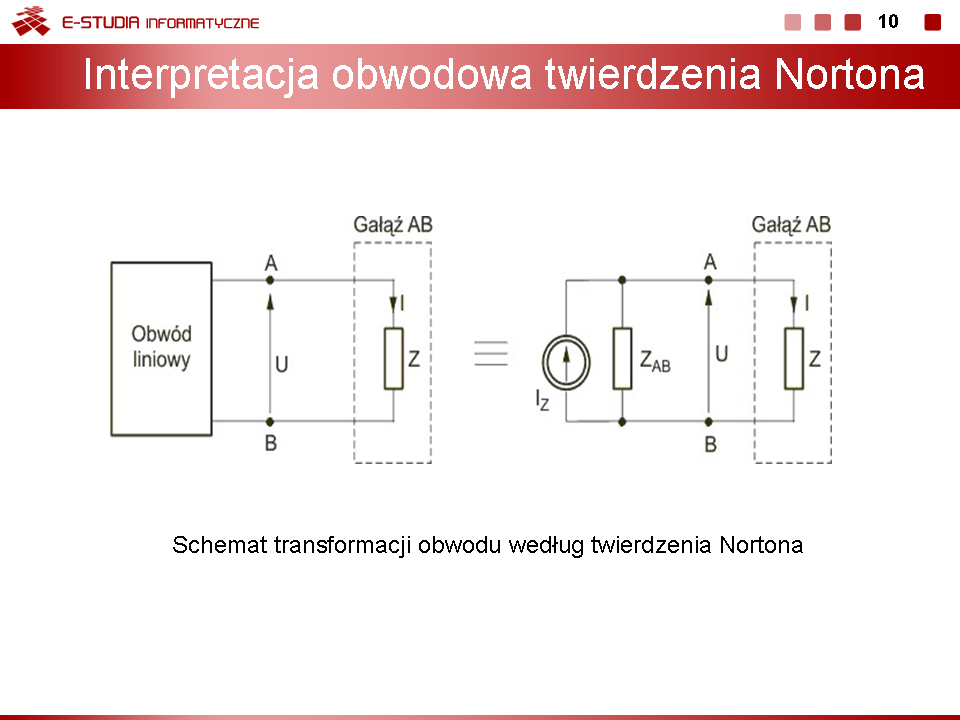
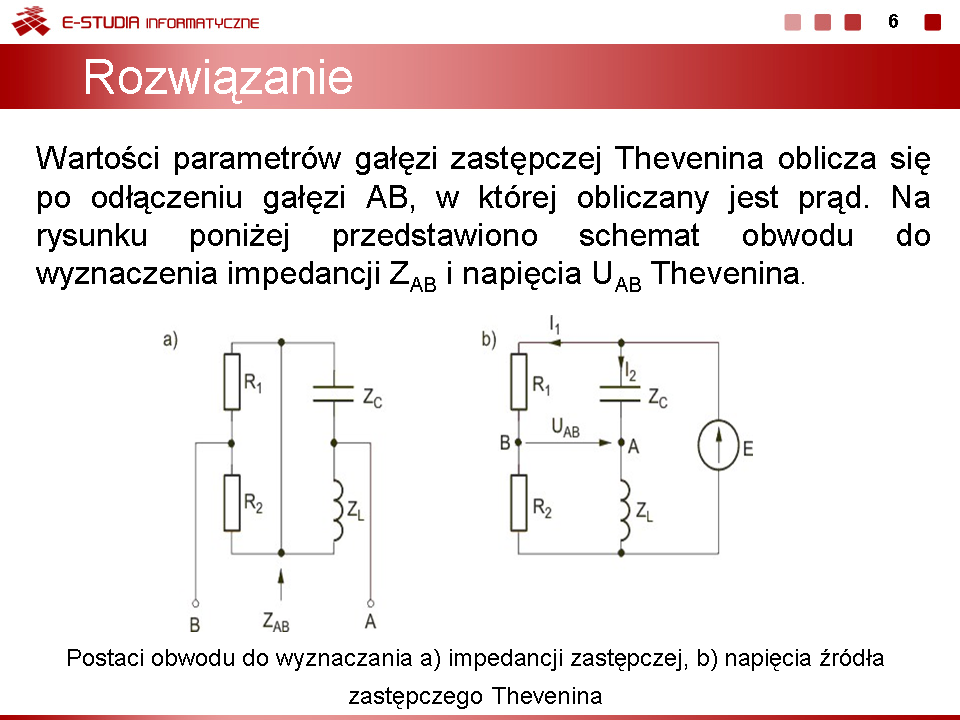
|valign="top"| | |valign="top"|W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: <math>Z_{AB}</math> i <math>U_{AB}</math>. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. | ||
|} | |} | ||
Wersja z 11:26, 24 sie 2006

|
Wykład 4. Metody analizy złożonych obwodów RLC w stanie ustalonym przy wymuszeniu sinusoidalnym |
|
W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: i . Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. |

|

|

|
Przykład
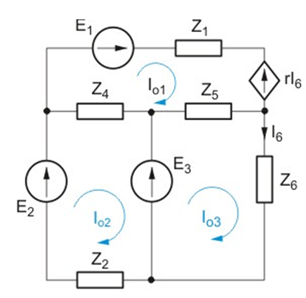
Dla obwodu przedstawionego na rysunku napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. |

|
| Zadania sprawdzające
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , . Rozwiązanie Impedancja z zacisków AB obwodu jest równa
Prądy w obwodzie z rys. b:
Napięcie
Poszukiwany prąd z obwodu zastępczego Thevenina (rys. c)
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci |