PEE Moduł 2

Wykład 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym

---

Parametry sygnału sinusoidalnego Sygnały sinusoidalne zwane również harmonicznymi są opisane w dziedzinie czasu następującym wzorem (w opisie przyjęto oznaczenie sygnału napięciowego) $u(t)=U_{m}sin(\omega t+\psi )$ Wielkości występujące w opisie mają następujące nazwy i oznaczenia: $u(t)$ - wartość chwilowa napięcia $U_m$ - wartość maksymalna (szczytowa) napięcia zwana również amplitudą $\psi$ - faza początkowa napięcia odpowiadająca chwili t=0 $\omega t+\psi$ - kąt fazowy napięcia w chwili t $f=1/T$ - częstotliwość mierzona w hercach (Hz) $T$ - okres przebiegu sinusoidalnego $\omega =2\pi f$ - pulsacja mierzona w radianach na sekundę. Wartości chwilowe sygnałów oznaczać będziemy małą literą a wartości maksymalne, skuteczne i wielkości operatorowe dużą. Rysunek na slajdzie obok przedstawia przebieg sygnału sinusoidalnego napięcia z oznaczeniami poszczególnych jego parametrów. Oś odciętych ma podwójne oznaczenie: czasu oraz fazy (aktualny kąt fazowy).

---

Przebiegi zmienne w czasie dobrze charakteryzuje wartość skuteczna. Dla przebiegu okresowego $f(t)$ o okresie $T$ jest ona definiowana w postaci Parser nie mógł rozpoznać (błąd składni): {\displaystyle F=\sqrt\left \frac{1}{T} \right \int_{t_0}^{t_o+T}f^2(t)dt } Łatwo udowodnić, że wartość skuteczna przebiegu okresowego nie zależy od wyboru fazy początkowej. W przypadku przebiegu sinusoidalnego napięcia $u(t)=U_{m}sin(\omega t+\psi )$ jest równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle U=\left \frac{U_m}{\sqrt 2} \right} a w przypadku prądu sinusoidalnego $i(t)=U_{m}sin(\omega t+\psi )$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle I=\left \frac{I_m}{\sqrt 2} \right} Dla sygnału sinusoidalnego wartość skuteczna jest więc $\sqrt{2}$ razy mniejsza niż jego wartość maksymalna. Należy zauważyć, że napięcie stałe $u(t)=U$ jest szczególnym przypadkiem sygnału sinusoidalnego, dla którego częstotliwość jest równa zeru $(f=0)$ a wartość chwilowa jest stała i równa $u(t)=U_{m}sin(\omega t+\psi )=U$. Jest to ważna właściwość, gdyż dzięki temu metody analizy obwodów o wymuszeniu sinusoidalnym mogą mieć zastosowanie również do wymuszeń stałych przy założeniu $f=0$. Dla sygnału stałego wartość maksymalna i skuteczna są sobie równe i równają się danej wartości stałej.

---

Metoda symboliczna liczb zespolonych analizy obwodów RLC w stanie ustalonym Analiza obwodów zawierających elementy RLC przy wymuszeniu sinusoidalnym napotyka na pewne trudności związane z wystąpieniem w opisie cewki i kondensatora równań różniczkowych. Trudności te łatwo jest pokonać w stanie ustalonym. Stanem ustalonym obwodu nazywać będziemy taki stan, w którym charakter odpowiedzi jest identyczny jak charakter wymuszenia, to znaczy odpowiedzią na wymuszenie sinusoidalne jest odpowiedź również sinusoidalna o tej samej częstotliwości choć o różnej amplitudzie i fazie początkowej. Dla stanu ustalonego obwodu wprowadzona zostanie metoda liczb zespolonych, zwana również metodą symboliczną, sprowadzająca wszystkie operacje różniczkowe i całkowe do działań algebraicznych na liczbach zespolonych.

---

Dla wprowadzenia tej metody przyjmijmy, że rozważany jest obwód szeregowy RLC zasilany ze źródła napięcia sinusoidalnego $u(t)=U_{m}sin(\omega t+\psi )$ Z prawa napięciowego Kirchhoffa wynika następujący związek między napięciami elementów tego obwodu $u(t)=u_R+u_L+u_C$ Biorąc pod uwagę podstawowe zależności definicyjne dla rezystora, cewki i kondensatora $u_R=Ri$ $u_c=\frac{1}{C}\int idt$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle u_L=L \left \frac{di}{dt} \right} otrzymuje się Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_m sin(\omega t+\psi)=R_i+ \left \frac{1}{C} \right \int idt+L \left \frac{di}{dt} \right}

---

Ostatni wzór przedstawia sobą równanie różniczkowo-całkowe opisujące zależności między wartościami chwilowymi prądu i napięcia wymuszającego w obwodzie. Pełne rozwiązanie tego równania sprowadza się do wyznaczenia dwu składowych prądu, stanowiących odpowiedź obwodu w stanie ustalonym i stanie przejściowym: składowej ustalonej, której charakter zmian w czasie jest taki sam jak sygnału wymuszającego (przy sinusoidalnym wymuszeniu odpowiedź również sinusoidalna o tej samej częstotliwości); jest to stan który zostanie osiągnięty przez obwód po czasie teoretycznie dążącym do nieskończoności. składowej przejściowej odpowiadającej różnicy między rozwiązaniem rzeczywistym równania różniczkowego a składową ustaloną. Składowa przejściowa zanika zwykle szybko w czasie i pozostaje jedynie składowa ustalona. Stan po zaniknięciu składowej przejściowej nazywamy stanem ustalonym obwodu.

---

Składową ustaloną prądu w obwodzie można otrzymać nie rozwiązując równania różniczkowego opisującego ten obwód a korzystając jedynie z metody liczb zespolonych (metody symbolicznej). Istotnym elementem tej metody jest zastąpienie przebiegów czasowych ich reprezentacją zespoloną. Przyjmijmy, że prąd $i(t)=I_{m}sin(\omega t+\psi )$ oraz napięcie $u(t)=U_{m}sin(\omega t+\psi )$ zastąpione zostały przez wektory wirujące w czasie, odpowiednio $I(t)$ oraz $U(t)$ określone w postaci $U(t)=U_m{e}^j{}^{\psi }{e}^j{}^{\omega }{}^t$ $I(t)=I_m{e}^j{}^{{\psi }_i}{e}^j{}^{\omega }{}^t$ Po zastąpieniu wartości czasowych prądu i napięcia poprzez ich reprezentację w postaci wektorów wirujących otrzymuje się Parser nie mógł rozpoznać (błąd składni): {\displaystyle U(t)=RI(t)+L \left \frac{dI(t)}{dt} \right+\frac{1}{C} \int I(t)dt}

---

Po wykonaniu operacji różniczkowania i całkowania równanie powyższe przyjmuje postać $\frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }=R\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}+j\omega L\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}+\frac{1}{j\omega C}\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ Oznaczmy przez $u=\frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }$ wartość skuteczną zespoloną napięcia, a przez $I=\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ wartość skuteczną zespoloną prądu. Wtedy równanie można zapisać w następującej postaci obowiązującej dla wartości skutecznych zespolonych $U=RI+j\omega LI+\frac{1}{j\omega C}I$

---

Wielkość $U_r=RI$ odpowiada napięciu skutecznemu zespolonemu na rezystorze, $U_L=j\omega LI$ reprezentuje wartość skuteczną zespoloną napięcia na cewce, $U_c=\frac{1}{j\omega C}I$ odpowiada wartości skutecznej zespolonej napięcia na kondensatorze. Wszystkie napięcia i prąd w obwodzie są wartościami zespolonymi.

---

Można zauważyć prostą analogię do równania opisującego obwód rezystancyjny. W tym celu wprowadzimy uogólnienie rezystancji w postaci pojęcia impedancji zespolonej wiążącej wartości skuteczne prądu i napięcia na elementach R, L, C w stanie ustalonym przy wymuszeniu sinusoidalnym. Z ostatnich równań na podstawie prawa Ohma można napisać następujące przyporządkowania: Dla rezystora $Z_R=R$ impedancja $Z_R$ jest równa rezystancji tego rezystora. Dla cewki $Z_L=j\omega L$ impedancja $Z_L$ jest liczbą zespoloną (urojoną) zależną liniowo od częstotliwości. Dla kondensatora $Z_C=\frac{1}{j\omega C}=-j\frac{1}{\omega C}$ impedancja $Z_C$ jest także zespolona i odwrotnie proporcjonalna do częstotliwości. $X_L=\omega L$ nosi nazwę reaktancji indukcyjnej, a $X_C=\frac{1}{\omega C}$ reaktancji pojemnościowej. W związku z powyższym można napisać $Z_L=j{X}_L,Z_C=-j{X}_C$.

---

Wprowadzając oznaczenie wypadkowej impedancji obwodu przez $Z$, gdzie $Z=Z_R+Z_L+Z_C$ zależność prądowo-napięciową w obwodzie szeregowym RLC można zapisać w postaci, znanej jako prawo Ohma dla wartości symbolicznych $U=ZL$ lub $I=\frac{U}{Z}=|I|e^j{}^w$ gdzie moduł prądu i kąt fazowy prądu dane są wzorami $|I|=\frac{|U|}{|Z|}=\frac{|U|}{{\sqrt{R}}^2+(\omega L-1/(\omega C){)}^2}$ ${\psi }_i=\psi -arctg\frac{\omega L-1/(\omega C)}{R}$ Faza początkowa wektora napięcia wymuszającego jest tu oznaczona przez $\psi$ , a faza początkowa wektora prądu – przez ${\psi }_i$ Różnica faz nazywana jest przesunięciem fazowym prądu względem napięcia i oznaczana literą $\phi$ , przy czym $\phi =\psi -{\psi }_i=arctg\frac{\omega L-1/(\omega C)}{R}$ Kąt przesunięcia fazowego $\phi$ odgrywa ogromną rolę w elektrotechnice, zwłaszcza w zagadnieniach mocy. Kąt ten jest uważany za dodatni dla obwodów o charakterze indukcyjnym a za ujemny dla obwodów o charakterze pojemnościowym. Zauważmy, że wartościom skutecznym zespolonym prądu oraz napięcia można przyporządkować funkcję czasu. Biorąc pod uwagę, że przejście z przebiegu czasowego na opis zespolony (symboliczny) odbywa się według schematu $u(t)=U_{m}sin(\omega t+\psi )\to \frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }$ powrót z wartości zespolonej do postaci czasowej polega na pomnożeniu modułu wartości skutecznej przez $\sqrt{2}$ i uzupełnieniu wyniku przez dopisanie funkcji$sin(\omega t+\psi )$ Stąd przykładowo, jeśli wynik zespolony prądu dany jest w postaci $I=10e^{50^o}$ , to odpowiadający mu przebieg czasowy ma postać $i(t)=10\sqrt{2}sin(\omega t+50^o)$ Istnieje również ścisła analogia między konduktancją (odwrotność rezystancji) a odwrotnością impedancji. Analogicznie do pojęcia konduktancji w obwodzie rezystancyjnym wprowadza się pojęcie admitancji zespolonej dla obwodu RLC. Admitancja jest definiowana jako odwrotność impedancji. Oznaczana jest najczęściej literą $Y$, przy czym $Y=1/Z$ Admitancja kondensatora jest równa $Y_C=j\omega C$ , cewki $Y_L=\frac{1}{j\omega L}=-\frac{1}{\omega L}$ natomiast admitancja rezystora jest równa jego konduktancji $Y_R=G=1/R$.

---

Prawa Kirchhoffa dla wartości symbolicznych Przy zastąpieniu wartości rzeczywistych przez wartości zespolone równania różniczkowe zostały zastąpione przez równania algebraiczne. Nastąpiła zatem algebraizacja równań opisujących obwód. Wszystkie elementy RLC traktowane są w podobny sposób i reprezentowane przez swoje impedancje symboliczne w postaci zespolonej. Impedancje zespolone mogą być interpretowane jako uogólnienie rezystancji. Dla obwodu reprezentowanego w postaci symbolicznej obowiązują prawa Kirchhoffa, które mają identyczną postać jak dla obwodu rzeczywistego, z tą różnicą, że zamiast wielkości chwilowych używa się wielkości zespolonych. Prawo prądowe Kirchhoffa Suma algebraiczna prądów zespolonych w dowolnym węźle obwodu elektrycznego jest równa zeru, co zapiszemy w postaci $\sum _k{l}_k=0$ W równaniu tym wszystkie prądy dane są w postaci zespolonej. Prawo napięciowe Kirchhoffa Suma algebraiczna napięć zespolonych w każdym oczku obwodu elektrycznego jest równa zeru, co zapiszemy w postaci $\sum _k{U}_k=0$ W równaniu tym symbolem $U$ oznaczono wszystkie napięcia w postaci zespolonej, zarówno na gałęziach pasywnych jak i źródłowych obwodu. Sposób sumowania (znak plus lub minus) zarówno prądów jak i napięć jest taki sam jak w przypadku operowania wartościami rzeczywistymi.

---

Podsumowując, na metodę symboliczną analizy obwodu składa się Przejście z przebiegu czasowego na opis zespolony (symboliczny) dla źródeł prądu i napięcia $u(t)=U_{m}sin(\omega t+{\psi }_u)\to \frac{U_m}{\sqrt{2}}{e}^j{}^{{\psi }_u}$ $i(t)=I_{m}sin(\omega t+{\psi }_i)\to \frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ Zastosowanie reprezentacji elementów poprzez ich impedancje zespolone Zastosowanie praw Kirchoffa dla wartości symbolicznych Rozwiązanie układu równań w postaci skutecznej zespolonej Ewentualnie (w miarę potrzeb) przedstawienie rozwiązania w postaci czasowej (odwrotna operacja) do wykonanej w punkcie pierwszym).

---

Wykresy wektorowe obwodu W przypadku analizy obwodów RLC w stanie ustalonym ważnym pojęciem jest wykres wektorowy, zwany również wykresem wskazowym, przedstawiający w sposób orientacyjny zależności między poszczególnymi wektorami prądu i napięcia w obwodzie. Jak wiadomo każdej liczbie zespolonej można przyporządkować reprezentację geometryczną w postaci odpowiedniej zależności wektorowej przedstawionej na płaszczyźnie, w której oś pozioma odpowiada części rzeczywistej a oś pionowa części urojonej liczby zespolonej. Konstruując wykres należy pamiętać, że pomnożenie wektora przez operator $j$ jest równoważne jego obrotowi o kąt 90 stopni przeciwnie do ruchu wskazówek zegara gdyż operator j jest równy $e^j{}^{90^o}$ Podobnie pomnożenie wektora przez operator $-j$ jest równoważne jego obrotowi o kąt 90 stopni zgodnie z ruchem wskazówek zegara gdyż operator -j jest równy $e^{-}{}^j{}^{90^o}$ Pomnożenie wektora przez liczbę rzeczywistą nie zmienia pozycji wektora w przestrzeni o ile jest to liczba dodatnia lub zmienia zwrot wektora o jeśli liczba ta jest ujemna. Z zależności prądowo-napięciowych dla rezystora jest oczywiste, że $U_R=R{I}_R$ co wobec rzeczywistych, dodatnich wartości R oznacza, że napięcie na rezystorze jest w fazie z prądem tego rezystora. Dla cewki obowiązuje Parser nie mógł rozpoznać (nieznana funkcja „\omeha”): {\displaystyle U_L=j\omeha LI_L} co oznacza, że napięcie na cewce wyprzedza prąd o kąt . Podobnie napięcie na kondensatorze opóźnia się względem swojego prądu o kąt , gdyż $U_C=-j\frac{1}{\omega C}{I}_C$ Rys. 2.3. Wykresy wektorowe dla a) rezystora, b) cewki, c) kondensatora

---

Przedstawione powyżej zasady konstruowania przesunięć kątowych między wektorami prądu i napięcia umożliwiają podanie ogólnych zasad postępowania przy konstruowaniu wykresu wektorowego dla dowolnego obwodu RLC. Wykres wektorowy z definicji uwzględnia przede wszystkim przesunięcia kątowe między poszczególnymi wektorami. Relacje ilościowe (długości) poszczególnych wektorów są mniej istotne i zwykle uwzględniane w sposób jedynie przybliżony. Wykres rozpoczyna się zwykle od końca obwodu (gałęzi najdalej położonej od źródła). Jeśli gałąź jest połączeniem szeregowym elementów rozpoczynamy od prądu tej gałęzi, a w przypadku połączenia równoległego – od napięcia. Następnie rysuje się na wykresie na przemian napięcia i prądy kolejnych gałęzi, dochodząc w ten sposób do źródła. Budowę wykresu kończy się w momencie dojścia do prądu i napięcia źródłowego obwodu. Relacja wektora prądu źródłowego względem napięcia decyduje o charakterze obwodu. Jeśli napięcie wypadkowe (źródłowe) wyprzedza prąd wypadkowy lub inaczej mówiąc prąd opóźnia się względem napięcia - obwód ma charakter indukcyjny. Jeśli natomiast napięcie opóźnia się względem prądu lub prąd wyprzedza napięcie - mówimy o charakterze pojemnościowym obwodu. Jeśli nie istnieje przesunięcie fazowe prądu wypadkowego względem napięcia (kąt fazowy równy zeru) mówimy o tzw. stanie rezonansu obwodu, lub po prostu charakterze rezystancyjnym danego obwodu. Charakter rezystancyjny obwodu może powstać nawet przy istnieniu w obwodzie indukcyjności i pojemności w przypadku gdy następuje kompensacja odpowiednich składowych indukcyjnej i pojemnościowej wektorów. Sposób postępowania przy sporządzaniu wykresów wektorowych przedstawimy na przykładzie konkretnego obwodu.

---

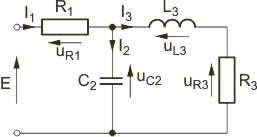
Przykład 2.1 Narysować wykres wektorowy prądów i napięć dla obwodu RLC o strukturze przedstawionej na rysunku

---

---

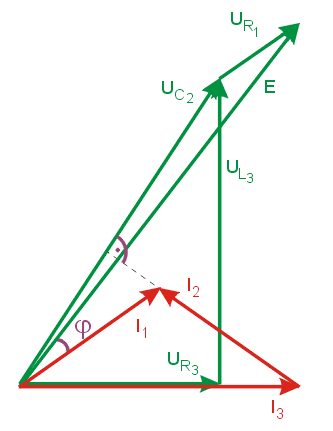
Rozwiązanie Na rysunku obok przedstawiono wykres wektorowy prądów i napięć w obwodzie RLC z z porzedniego slajdu Sporządzanie wykresu rozpoczyna się od prądu I3 dobudowując kolejno wektory napięć i prądów gałęzi przesuwając się w stronę źródła: $U_{R_3},U_{L_3},U_{R_2},I_2,I_1,U_{C_1},E$. Jak widać obwód ma charakter pojemnościowy, gdyż napięcie wypadkowe E opóźnia się względem odpowiadającego mu prądu $I_1$

---

Zadania sprawdzające Zadanie 2.1 Wyznaczyć rozpływy prądów w obwodzie z rysunku w stanie ustalonym. Przyjąć następujące wartości parametrów: $i(t)=5\sqrt{2}sin(1000t)A,R=10\mathrm{\Omega },c=0,0001F,l=5mH$

---

Rozwiązanie Wartości symboliczne elementów obwodu: $\omega =1000$ $I=5$ $z_L=j\omega L=j5$ $Z_C=\frac{1}{j\omega C}=-j10$ Impedancje obwodu RLC: $Y=\frac{1}{R}+\frac{1}{Z_L}+\frac{1}{Z_C}=0,1-j0,1$ $Z=\frac{1}{Y}=\frac{10}{\sqrt{2}}{e}^j{}^{45^o}$

---

Prądy i napięcie w obwodzie: $U=ZI=\frac{50}{\sqrt{2}}{e}^j{}^{40^o}$ $I_R=\frac{U}{R}=\frac{5}{\sqrt{2}}{e}^j{}^{40^o}$ $I_L=\frac{U}{Z_L}=\frac{10}{\sqrt{2}}{e}^{-}{}^j{}^{40^o}$ $I_C=\frac{U}{Z_C}=\frac{5}{\sqrt{2}}{e}^j{}^{135^o}$

---

---

Wartości chwilowe prądów i napięcia $u(t)$ $I_R=\frac{U}{R}=\frac{5}{\sqrt{2}}{e}^j{}^{40^o}$ $I_L=\frac{U}{Z_L}=\frac{10}{\sqrt{2}}{e}^{-}{}^j{}^{40^o}$ $I_C=\frac{U}{Z_C}=\frac{5}{\sqrt{2}}{e}^j{}^{135^o}$

---

Zadanie 2.2 Wyznaczyć prądy i napięcia w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów: $e(t)=20\sqrt{2}sin(100t-90^o)V,R_1=10\mathrm{\Omega },R_2=5\mathrm{\Omega },C=0,001F,L=0,00H$ Rozwiązanie Wartości symboliczne elementów obwodu: $\omega =100$ $E=20e^{-}{}^{90^o}$ $Z_L=j\omega L=j5$ $Z_C=1/j\omega C=-j10$ Impedancje obwodu: $Z_{R}L=\frac{R_2{Z}_L}{R_2+Z_L}=2,5+j2,5$ $Z=Z_{R}L+R_1+Z_C=12,5-j7,5$ Prądy i napięcia w obwodzie: $I=E/Z=0,71-j1,18$ $U_{R}L=I{Z}_{R}L=4,71-J1,18$ $I_1=\frac{U_{R}L}{R_2}=-0,23-j0,94$ $I_2=\frac{U_{R}L}{R_2}=-0,94-j0,23$ $U_C=I{Z}_C=-11,76-j7,06$ $U_{R_1}=I{R}_1=7,1-j11,8$ 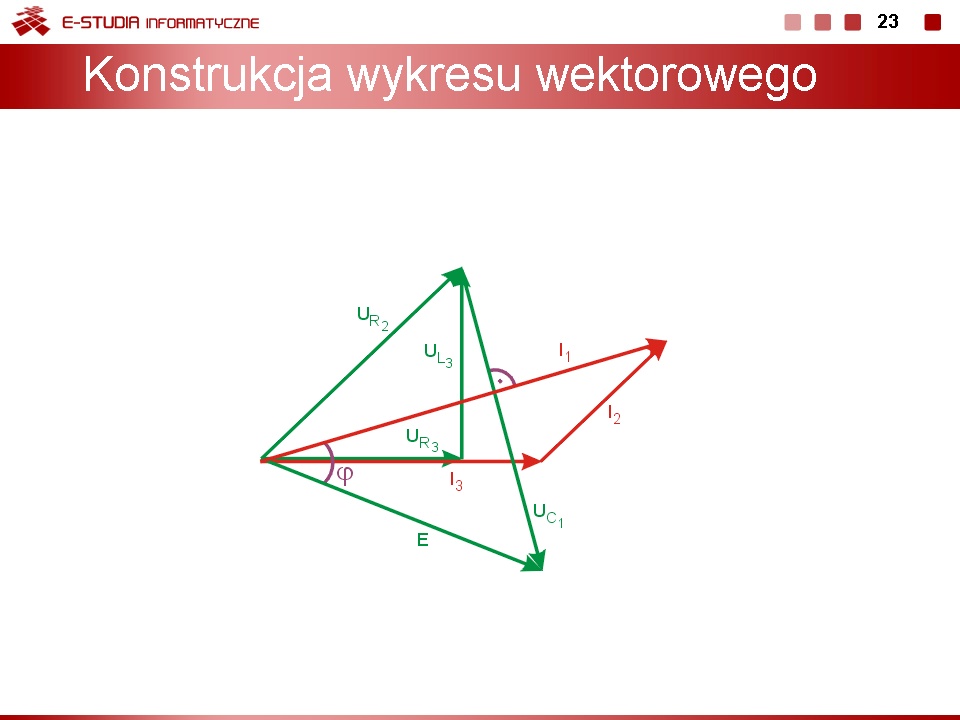Zadanie 2.3 Sporządzić wykres wektorowy prądów i napięć w obwodzie przedstawionym na rysUNKU Rozwiązanie Wykres rozpoczyna się od prądu $I_3$, dodając kolejno napięcia na $R_3$ i $L_3$, napięcie $U_C{}_2$, prąd $I_C{}_2$, prąd $I_1$ oraz napięcie $E$. Pełny wykres wektorowy przedstawiony jest na rysunku. Kąt fazowy przesunięcia prądu względem napięcia zasilającego jest równy $\phi$ Biorąc pod uwagę, że napięcie wyprzedza prąd obwód ma charakter indukcyjny.

---