PEE Moduł 2: Różnice pomiędzy wersjami
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| Linia 81: | Linia 81: | ||
Biorąc pod uwagę podstawowe zależności definicyjne dla rezystora, cewki i kondensatora | Biorąc pod uwagę podstawowe zależności definicyjne dla rezystora, cewki i kondensatora | ||
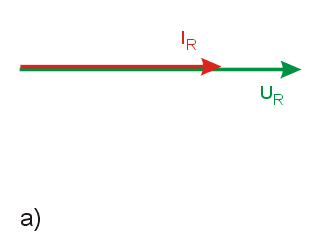
<math>u_R=Ri</math> | <math>u_R=Ri</math> | ||
| Linia 87: | Linia 88: | ||
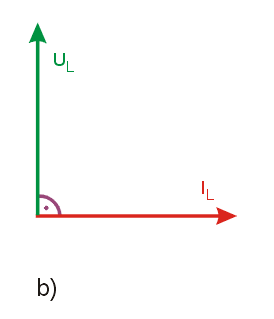
<math>u_L=L \left \frac{di}{dt} \right</math> | <math>u_L=L \left \frac{di}{dt} \right</math> | ||
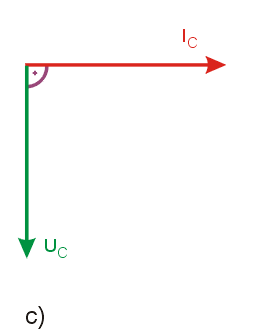
otrzymuje się | otrzymuje się | ||
| Linia 98: | Linia 100: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M2_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M2_Slajd6.png]] | ||
|valign="top"| | |valign="top"|Ostatni wzór przedstawia sobą równanie różniczkowo-całkowe opisujące zależności między wartościami chwilowymi prądu i napięcia wymuszającego w obwodzie. Pełne rozwiązanie tego równania sprowadza się do wyznaczenia dwu składowych prądu, stanowiących odpowiedź obwodu w stanie ustalonym i stanie przejściowym: | ||
#składowej ustalonej, której charakter zmian w czasie jest taki sam jak sygnału wymuszającego (przy sinusoidalnym wymuszeniu odpowiedź również sinusoidalna o tej samej częstotliwości); jest to stan który zostanie osiągnięty przez obwód po czasie teoretycznie dążącym do nieskończoności. | #składowej ustalonej, której charakter zmian w czasie jest taki sam jak sygnału wymuszającego (przy sinusoidalnym wymuszeniu odpowiedź również sinusoidalna o tej samej częstotliwości); jest to stan który zostanie osiągnięty przez obwód po czasie teoretycznie dążącym do nieskończoności. | ||
#składowej przejściowej odpowiadającej różnicy między rozwiązaniem rzeczywistym równania różniczkowego a składową ustaloną. | #składowej przejściowej odpowiadającej różnicy między rozwiązaniem rzeczywistym równania różniczkowego a składową ustaloną. | ||
Składowa przejściowa zanika zwykle szybko w czasie i pozostaje jedynie składowa ustalona. Stan po zaniknięciu składowej przejściowej nazywamy stanem ustalonym obwodu. | Składowa przejściowa zanika zwykle szybko w czasie i pozostaje jedynie składowa ustalona. Stan po zaniknięciu składowej przejściowej nazywamy stanem ustalonym obwodu. | ||
| Linia 117: | Linia 122: | ||
<math>I(t)=I_m e^j^{\psi_i} e^j^\omega ^t</math> | <math>I(t)=I_m e^j^{\psi_i} e^j^\omega ^t</math> | ||
Po zastąpieniu wartości czasowych prądu i napięcia | |||
Po zastąpieniu wartości czasowych prądu i napięcia poprzez ich reprezentację w postaci wektorów wirujących otrzymuje się | |||
Wersja z 08:19, 24 sie 2006

|
Wykład 2 Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym |

|
Przedstawione powyżej zasady konstruowania przesunięć kątowych między wektorami prądu i napięcia umożliwiają podanie ogólnych zasad postępowania przy konstruowaniu wykresu wektorowego dla dowolnego obwodu RLC.
|

|
Przykład 2.1
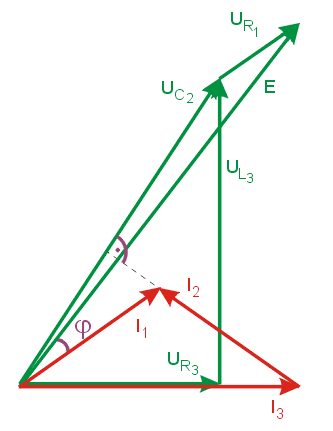
Narysować wykres wektorowy prądów i napięć dla obwodu RLC o strukturze przedstawionej na rysunku |
|
Rozwiązanie
Na rysunku obok przedstawiono wykres wektorowy prądów i napięć w obwodzie RLC z z porzedniego slajdu Sporządzanie wykresu rozpoczyna się od prądu I3 dobudowując kolejno wektory napięć i prądów gałęzi przesuwając się w stronę źródła: . Jak widać obwód ma charakter pojemnościowy, gdyż napięcie wypadkowe E opóźnia się względem odpowiadającego mu prądu |

|
Zadania sprawdzające
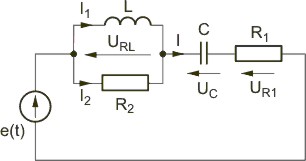
Zadanie 2.1 Wyznaczyć rozpływy prądów w obwodzie z rysunku w stanie ustalonym. Przyjąć następujące wartości parametrów: |

|
Rozwiązanie
Wartości symboliczne elementów obwodu:
Impedancje obwodu RLC:
|

|
Prądy i napięcie w obwodzie:
|

|
Wartości chwilowe prądów i napięcia
|
| Zadanie 2.2
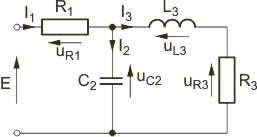
Wyznaczyć prądy i napięcia w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów:
Wartości symboliczne elementów obwodu:
Impedancje obwodu:
Prądy i napięcia w obwodzie:
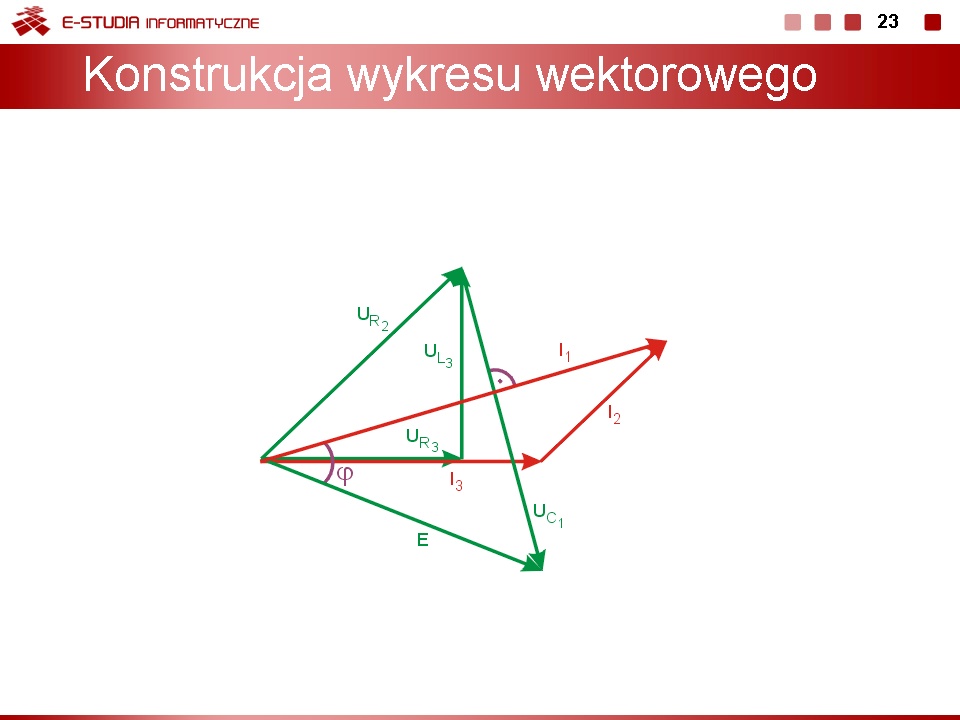
Zadanie 2.3 Sporządzić wykres wektorowy prądów i napięć w obwodzie przedstawionym na rysUNKU
Rozwiązanie Wykres rozpoczyna się od prądu , dodając kolejno napięcia na i , napięcie , prąd , prąd oraz napięcie . Pełny wykres wektorowy przedstawiony jest na rysunku.
Kąt fazowy przesunięcia prądu względem napięcia zasilającego jest równy Biorąc pod uwagę, że napięcie wyprzedza prąd obwód ma charakter indukcyjny. |